Методика изучения избранного геометрического материала

10.3.1. Методика изучения темы: «Соотношения между сторонами и углами прямоугольного треугольника».

Покажем, каким образом может быть организовано изучение указанной темы, используя опыт учителей математики (И.А. Адрова, И.В. Ромашко) школы № 37 г. Москвы.

Выше неоднократно подчеркивалось, что при организации учебного процесса в классах КРО необходимо учитывать особенности учащихся: слабое здоровье, что ведет к повышенной утомляемости; медленный темп учебной деятельности; недостаточное развитие психических и психофизических функций (произвольного внимания, произвольного запоминания, логического и абстрактного мышления); недостаточная сформированность обще­учебных навыков; низкий уровень мотивации и т.п.

Изучив различные технологии личностно ориенти­рованного подхода, учителя математики московской школы № 37 разработали систему работы на уроке, которая состоит из следующих этапов.

1. Ознакомление учащихся с целями обучения.

2. Актуализация основных теоретических понятий (работа в парах).

3. Диагностический тест (проверка готовности к восприятию нового материала).

4. Коррекция.

5. Обучение с использованием различных форм, методов, включающих каждого ученика в активную деятельность.

6. Итоговый тест, позволяющий оценить результат обучения каждого ученика.

7. Уровневое домашнее задание.

Работа учащегося в течение всего урока оценивается по рейтинговой системе. На каждом этапе ученик получает определенное количество баллов. В конце урока подсчитывается число баллов за урок, и каждый ученик получает оценку. Использование рейтинговой системы активизирует деятельность каждого ученика. Работа в парах позволяет развивать у обучаемых самостоятельность и коммуникативность. В процессе речи развиваются навыки мыслительной деятельности, включается работа памяти. Ведущей идеей построения системы является создание педагогических условий для включения каждого ученика в деятельность, соответствующую его зоне ближайшего развития.

И.А. Адрова и И.В. Ромашко предлагают следующую организацию изучения темы «Соотношения между сторонами и углами прямоугольного треугольника».

Урок № 1. Изучение и первичное закрепление понятий: прилежащий катет и противолежащий катет острого угла в прямоугольном треугольнике; определения синуса, косинуса и тангенса острого угла в прямоугольном треугольнике; вычисления значений этих функций в простейших случаях.

Урок № 2. Закрепление понятий, рассмотренных на уроке № 1. Вычисление значений синуса, косинуса и тангенса углов 30°, 45°, 60°.

Урок № 3. Изучение и первичное закрепление тригонометрического метода решения прямоугольных треугольников. Формирование навыков и использование знаний и умений, рассмотренных на уроках № 1 и 2. Нахождение неизвестных элементов прямоугольного треугольника по: катету и противолежащему углу; катету и прилежащему острому углу.

Урок № 4. Ознакомление с таблицами тригонометрических функций и их применение к решению задач. Решение задач на нахождение неизвестных элементов прямоугольного треугольника по: катету и гипотенузе; двум катетам.

Урок № 5. Решение задач.

Как видно из приведенного плана, основным является урок № 1 по данной теме. Представим его подробное описание.

Урок № 1. Определения синуса, косинуса и тангенса острого угла в прямоугольном треугольнике.

Организационный момент.

Мотивация. Объяснение учителя: «В практической жизни очень часто встречаются задачи, связанные с измерением геометрических величин – длины, площади и т.д. Многие приемы непосредственного измерения были изобретены еще в глубокой древности. Однако не всякая величина может быть измерена непосредственно. (Например, как измерить высоту солнца над горизонтом? Как определить длину моста, который надо построить через реку?) Поэтому люди стали находить другие способы измерения величин. Накопление и систематизация некоторых вычислительных методов решения геометрических задач привели к созданию нового раздела математики, который в 16 веке назвали тригонометрией. Слово «тригонометрия» произошло от греческих слов «тригонон» – «треугольник» и «метрейн» – «измерять», т.е. дословно его можно перевести как «измерения треугольников». Действительно, изучая треугольники, люди научились определять недоступные расстояния, например, такие:

1. С башни маяка высотой 70 м виден корабль под углом 3° к горизонту. Каково расстояние от корабля до маяка?

2. Найти угол подъема шоссейной дороги, если на расстоянии 200 м высота подъема составила 6 м.

3. Строение дает тень 15 м, когда высота солнца равна 60°. Определить высоту этого строения.

Изучив данную тему, мы с вами тоже научимся решать такие задачи».

R

Актуализация знаний. Подготовка к восприятию нового материала. Учитель задает классу вопросы: «Какой из данных на рисунке 8 треугольников прямоугольный? Какой треугольник называется прямоугольным?»

Изобразите в своих тетрадях прямоугольный треугольник ABC, у которого угол C прямой. (В тетрадях появляется рисунок 9).

Вопросы учителя: «Как называется сторона AB? Как называется сторона BC? Какая сторона прямоугольного треугольника называется гипотенузой, катетом? Какой катет является противолежащим углу A (углу B)? Какой катет является прилежащим к углу A (углу B)?»

В тетрадях учащихся должны остаться следующие записи:

_____________

Δ ABC C=90°

AB – гипотенуза; AC, BC –катеты

Противолежащий катет Прилежащий катет

Для угла А ВС АС

Для угла В АС ВС

______________

Самостоятельная работа. Одно и то же задание предъявляется классу в разных формах. Одни учащиеся выполняют его как математический диктант, т.е. воспринимая вопросы на слух, другим учитель вручает заранее приготовленные листы с вопросами.

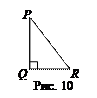1. По рисунку 10 назовите:

а) гипотенузу ­_______(1 балл);

б) катеты ___________(1 балл);

в) катет, противолежащий

углу Р_________(1 балл);

г) катет, прилежащий к

углу R _________(1 балл).

2. Продолжите предложение: сторона прямоугольного треугольника, лежащая против угла в 90°, называется _______ (1 балл).

3. Продолжите предложение: стороны прямоугольного треугольника, образующие прямой угол, называются _______ (1 балл).

Самопроверка. Верные ответы записаны заранее на закрытой части доски. В конце работы эта часть доски открывается, учащиеся видят, где они ошиблись, и сами себе выставляют баллы на полях тетради.

Изучение нового материала проводится одновременно в трех формах, учащиеся сами выбирают ту форму, по которой они лучше усваивают материал, в зависимости от того, кто они: визуалы, кинестетики или аудиалы.

Одна группа учащихся только слушает учителя, другая – слушает и делает записи в тетрадях, третья – слушает учителя и одновременно читает учебник, четвертая – читает учебник, пятая – читает учебник и делает записи в тетради.

Учитель на доске, а учащиеся в тетради составляют в своих тетрадях таблицу.

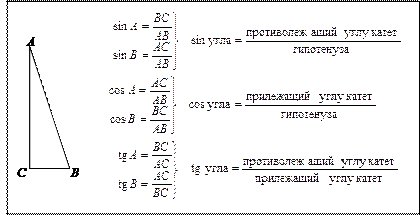Пауза релаксации. Дети отдыхают.

Закрепление нового материала.

Задание. Сформулировать определения синуса, косинуса, тангенса острого угла в прямоугольном треугольнике (за каждое определение 1 балл). Учащиеся проверяют друг друга, работая в парах. При этом проверяющий может пользоваться учебником, записями в тетрадях. Отвечающий ученик сначала пробует ответить самостоятельно, по памяти, но если он затрудняется, то использует таблицу в тетради (тогда он получает за ответ 0,5 балла). Учащиеся оценивают друг друга.

Q

Устная работа по готовым чертежам (рис. 11).

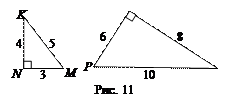Найдите синусы, косинусы, тангенсы острых углов треугольников.

R

За каждый ответ учащийся получает 1 балл. Практически все учащиеся должны ответить хотя бы на один вопрос.

Результаты записываются на доске.

__________________________

sin M = 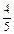sin K = 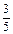sin P = 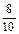= 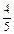sin R = =

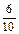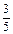
cos M = 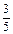cos K = 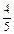cos P = 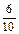= 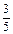cos R = =

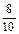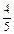
tg M = 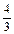tg K = 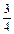tg P = 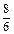= 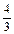tg R = =

__________________________

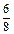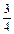
Самостоятельная работа по вариантам. Найдите:

1 вариант: 2 вариант:

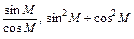
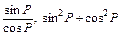
Каждый вариант выполняет на доске один из учащихся.

После проверки учитель задает вопросы: «С каким значением в таблице совпал ответ при нахождении отношения синуса угла к косинусу? Какое предположение можно сделать о сумме квадратов синуса и косинуса одного угла?»

В результате обсуждения ответов в тетрадях учащихся должны появиться формулы: tg А =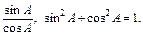

Контроль за усвоением нового материала проводится с помощью практической работы.

Задания.

Начертить прямоугольный треугольник PNR, R = 90° (1 балл).

Измерить катеты треугольника в мм. Записать, чему равны PN и NR (1 балл).

Записать, чему равна PR (1 балл).

Найти sin P, cos R, tg P (1 балл).

A

Дополнительное задание. По рисунку 12 найти sin А, cos А (3 балла).

Рис. 12

Проходя по рядам, учитель быстро проверяет и оценивает работы.

Подведение итогов урока. Суммирование набранных баллов, выставление оценки за урок. Если ученик набрал от 16 до 21 балла, то его оценка – «отлично», от 11 до 16 баллов – оценка «хорошо», от 10 до 11 баллов – оценка «удовлетворительно». Если ученик получил меньше 10 баллов, значит, он плохо работал на уроке.

10.3.2. Методика формирования понятия «Смежные углы».

Определение смежных углов имеет два существенных свойства: наличие у обоих углов общей стороны и то, что вторые стороны этих углов являются дополнительными полупрямыми.

Учащимся предъявляется рисунок 13:

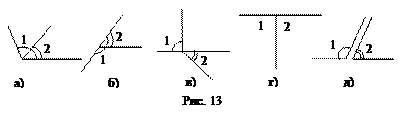
Далее процесс восприятия и осознания направляется вопросами учителя по предложенным рисункам:

– Назовите рисунки, на которых изображены два угла, имеющие одну общую сторону.

– Назовите рисунки, на которых сторона одного угла является дополнительной полупрямой для стороны другого угла.

– На каких рисунках изображены углы, которые одновременно удовлетворяют двум предъявленным требованиям?

Далее учитель сообщает термин «смежные углы», формулирует соответствующее определение. Для закрепления выделенных существенных свойств учитель дает задание обосновать, почему углы на рисунках а), в) и д) не являются смежными. Рассматривается, чем различаются смежные углы на рисунках б) и г) и чем вообще могут отличаться друг от друга пары смежных углов.

Психологами (М.А. Холодная и др.) установлено, что при изучении всякого понятия должно быть установлено соответствие нового знания личному интеллектуальному опыту учащихся, в котором могут содержаться противоречия с новыми знаниями. С отношением «быть смежными» многие из учащихся встречались в быту, на уроках труда: смежные – соседние участки земли, помещения. Необходимо подчеркнуть сходство и различие вновь вводимого понятия с имеющимися.

Далее выполняются упражнения на усвоение определения понятия смежных углов. К ним относятся упражнения: а) на построение смежных углов; б) на распознавание смежных углов (подведение объекта под понятие); в) на выведение следствий из факта принадлежности данных углов к смежным углам; комбинированные.

1. Какие из углов, изображенных на рисунке 14, являются смежными?

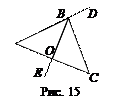
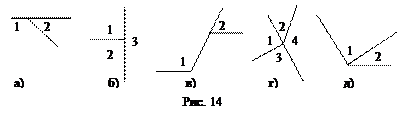2. Углы AОB и AОD – смежные. Что из этого следует?

3. Начертите несколько смежных углов.

А

4. Известно, что у двух углов общая сторона. Будут ли эти углы смежными? Ес­ли нет, то измените условие так, чтобы из него вытекало, что данные углы смежные.

5. Выделите на рисунке 15 смежные углы.

Упражнение 5 ориентировано на формирование умения выделять смежные углы на сложных рисунках. При этом осуществляется и овладение такими действиями, как переосмысление элементов чертежа с точки зрения других понятий (например, отрезки ОА и ОС мыслятся как дополнительные лучи, сторона ОВ треугольника АОВ – как сторона треугольника ОВС, а также как луч – сто­рона углов ОВА и OBD и т.д.), переход от существенных свойств понятия к термину и обратно и т. д.

На этапе применения понятия смежных углов выполняют­ся упражнения на использование определения для установле­ния различных зависимостей.

Вот примеры таких упражнений.

6. Лучи АС и AD дополнительные. Угол BAD равен 50°. Найдите угол ВАС.

7. Один из углов, образуемых при пересечении двух пря­мых равен 40°. Найдите все другие углы, полученные при пе­ресечении этих прямых.

На этапе выявления связей понятия смежных углов с ра­нее изученными понятиями можно предложить упражнения на составление «родословной» понятия. Приведем пример такого упражнения.

8. Составьте «родословную» понятия смежных углов (рис. 16).

Решение.

Можно использовать упражнения на установление связей между заданными понятиями. Например.

9. Между указанными в схеме (рис.17) понятиями укажите связи, характерные для определения смежных углов:

10.3.3. Методика работы с аксиомой о расположении трех точек на прямой.

Приведем фрагмент урока по введению аксиомы о расположении трех точек на прямой.

Введение аксиомы

На рисунке 18 отметьте точку С так, чтобы она лежала между точками А и В.

На каком рисунке местоположение точки С вы затруднились определить? Почему?

Придумайте рисунки, на которых точки А, В и С можно охаракте­ризовать следующим образом: только точка С лежит между точ­ками А и В.

Формулировка аксиомы

Сформулируйте свойство, общее для всех данных рисунков.

Сверьте сформулированное вами свойство с тем, что дано в учебнике.

Логический анализ формулировки аксиомы

О каких геометрических фигурах говорится в данном основном свойстве?

Что именно говорится о прямой и этих трех точках?

Какими другими словами можно заменить слова: «из трех точек на прямой»?

Как вы понимаете слова: «одна и только одна»?

Вопросы и задачи для закрепления аксиомы

1. Верно ли, что из трех точек одна и только одна лежит между двумя другими?

2. Верно ли, что для точек на прямой одна и только одна лежит между двумя другими?

3. Логическая задача. Три черепахи А, В и С соревнуются в спортивном ползании. Черепаха А говорит: «Я первая!» В: «Я вто­рая!» С: «Я не последняя!» Объясните.

10.3.4. Изучение теоремы «В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой».

1 этап. Чтобы учащиеся «открыли» сами содержание теоремы и сформулировали ее, проводится такая практическая работа. Перед уроком дается на дом задание: начертить три равно­бедренных треугольника (остроугольный разносторонний, прямоугольный и тупоугольный) и в этих треугольниках по­строить медианы и высоты к боковым сторонам (с помощью масштабной линейки и угольника), биссектрисы углов при ос­новании (с помощью транспортира). А на уроке предлагается по вариантам выполнить другую практическую работу: на­чертить в тетрадях равнобедренный треугольник (I вариант – остроугольный, II вариант – прямоугольный, III вариант – тупоугольный) и построить медиану и высоту к основанию и биссектрису угла при вершине, противолежащей основанию. Трое учащихся (по одному от каждого варианта) выполняют эту работу на доске. Учитель тем временем может построить разносторонний треугольник и провести в нем медианы, вы­соты и биссектрисы (этот рисунок можно заготовить заранее).

После выполнения практической работы обсуждаются ее результаты. У учащихся в каждом из данных случаев медиана, проведенная к основанию равнобедренного треугольника, яв­ляется биссектрисой и высотой.

Ставятся вопросы.

– Обладает ли этим свойством медиана, проведенная из вер­шин двух других углов равнобедренного треугольника к про­тиволежащей стороне? Нет. Это видно из рисунков, выпол­ненных в домашней практической работе.

– Обладают ли этим свойством медианы, проведенные в разностороннем треугольнике? Нет. (Учитель демонстрирует свой рисунок). Итак, практическим путем установлен новый факт. Какой? Учащиеся формулиру­ют теорему. Если есть необходимость, учитель уточняет их от­веты.

Мотивируется необходимость доказательства теоремы. Примерный диалог с учащимися:

– Во всех ли равнобедренных треугольниках медиана, проведенная к основанию, является биссектрисой и высотой?

– Неизвестно. В тех, которые рассматривались, да. А в других неизвестно.

– Как быть?

Делается вывод о том, что необходимо доказать справедли­вость теоремы для любого равнобедренного треугольника.

2 этап. Проводится работа над структурой теоремы: вы­деляется условие, заключение, еще раз уточняется, что теоре­ма сформулирована для равнобедренного треугольника. На доске и в тетрадях выполняется чертеж (рис. 19), записывается, что дано и что требуется доказать.

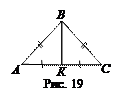Дано: Δ ABC – равнобедренный,

BК – медиана, проведенная к основанию.

Доказать: 1) BК – биссектриса,

2) BК – высота.

Поиск доказательства теоремы осуществляется движением от заключения к условию, т. е. аналитически.

Записывается доказательство теоремы.

Доказательство.

1) AB=BC (по определению равнобедренных треугольников), AК=КC (по определению медианы), BAК = BCК (по свойству равнобедренного треугольника). Следовательно, Δ ABК = Δ CBК (по первому признаку равенства треугольников).

2) Из определения равных треугольников ABК = CBК.

3) По определению биссектрисы BК – биссектриса ABC (1 утверждение доказано).

4) Δ ABК = Δ CBК, значит, по определению равных треугольников, BКA = BКC.

5) BКA и BКC – смежные (по определению смежных углов), следовательно, BКA + BКC = 180°.

6) Так как BКA = BКC и BКA + BКC = 180°, то BКA и BКC – прямые.

7) По определению перпендикулярных прямых BК перпендикулярна AC.

8) По определению высоты треугольника BК – высота (2–доказано).

3 этап. Усвоение формулировки теоремы может быть организовано посредством выполнения заданий.

1. Верно ли сформулирована теорема: «Медиана, проведенная к основанию, является биссектрисой и высотой»? Почему?

2. Вставьте пропущенные слова: «В ... треугольнике медиана, проведенная ..., является ... и ...». Текст проецируется через кодоскоп.

3. Сформулируйте теорему со словами: «Если ..., то ...».

Усвоение доказательства теоремы производится с помощью следующих вопросов и упражнений.

1. Какие понятия используются в формулировке теоремы?

2. Какие следствия использовались в процессе доказательства теоремы, например, из факта: «Δ ABC – равнобедренный»?

3. Назовите теоремы, которые использовались при доказа­тельстве данной теоремы. Какова цель их использования?

4. Докажите теорему, используя приведенную ниже структурную схему доказательства (рис. 20).

Рис. 20

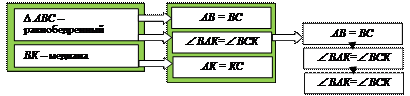
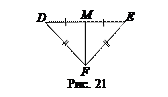5. Докажите теорему по рисунку 21.

4 этап. Решение задач на применение теоремы.

1. Точка М принадлежит высоте равнобедренного треугольни­ка, проведенной к основанию. Принадлежит ли эта точка: а) биссектрисе угла при вершине? б) медиане, проведенной к основанию? Почему?

2. Точка Р принадлежит биссектрисе угла треугольника. Принадлежит ли эта точка высоте треугольника? Почему?

3. Можно ли с помощью только масштабной линейки постро­ить биссектрису угла при вершине равнобедренного тре­угольника? Высоту? Дайте обоснование ответа.

4. Длина медианы равнобедренного треугольника, проведен­ной к основанию, равна 10см.Чему равны длины биссек­трисы и высоты, проведенных из той же вершины?

5. Докажите, что в равностороннем треугольнике биссектриса каждого из углов является медианой и высотой, проведен­ными из вершины угла, к противоположной стороне. Будут ли равны все биссектрисы, медианы и высоты между со­бой?

C

A

6. Решите задачи по готовым чертежам (рис. 22):

C

7. В равнобедренном треугольнике ABC с основанием AC проведена биссектриса BD. Найдите ее длину, если периметр треугольника ABC равен 50 см, а треугольника ABD – 40 см.

Задания

1. Выберите конкретную тему коррекционно-развивающего курса геометрии основной школы. Изучите соответствующие разделы программы и учебника. Выявите методические особенности изучения темы. Разработайте фрагменты методики обучения теме. Подготовьте комплект карточек для коррекции знаний учащихся.

2. Посетите несколько уроков геометрии одного из специальных (коррекционных) учреждений VII вида вашего региона. Проведите анализ одного урока с точки зрения его образовательной, коррекционно-развивающей, воспитательной и практической направленности.

ТВОРЧЕСКИЕ задания