Обучение математике особенных младших школьников

В Программно-методических материалах по коррекционно-развивающему обучению в начальной школе [22] отмечается, что обучение начальному курсу математики строится на том фундаменте элементарных математи­ческих знаний, которые дети приобретают в дошкольном периоде своей жизни, общаясь со сверстниками и взрослыми, действуя с различными предметными множествами. К моменту поступления в школу многие дети легко называют числа по порядку от 1 до 10 и дальше, знают цифры и геометрические фигуры, умеют выполнять несложные счет­ные операции в пределах первого десятка, могут решать простые арифметические задачи на нахождение суммы и остатка, владеют определенными графическими и измерительными умениями.

Другая часть детей к моменту поступления в школу не располагает элементарными математическими зна­ниями и умениями, которыми владеют их сверстники. У этих детей гораздо меньше диапазон счета: в то время как многие первоклассники называют числа до 20 и даже до 100, встречаются дети, которые не умеют правильно вос­произвести числовой ряд от 1 до 10. При пересчете кон­кретных предметов часть детей, называя итог, показывает лишь последний по счету предмет вместо всей группы, т. е. не отличает процесс счета от его результата. Если нужно посчитать от одного заданного числа до другого, они начинают с единицы и не умеют заканчивать счет на заданном числе. Особенно затрудняет таких детей счет в обратном порядке: дети сбиваются на прямой счет, пропускают чис­лительные. Дети лишь механически запоминают последовательность чисел, не умеют свободно ориентироваться в числовом ряду.

Обычно дети, имеющие пониженную математическую подготовку, в процессе счета пользуются развернутыми внешними действиями: передвигают предметы или дотра­гиваются до них, вслух называют числительные, в то время как большинство детей уже считают предметы «глазами». Значительные затруднения вызывает у этих детей срав­нение двух групп предметов. Определить разностные отношения они могут только в тех случаях, когда предметы в группах взаимно-однозначно (наглядно) соотнесены.

Следует отметить значительное отставание навыков счета у детей. В самом начале обучения они ориентируются лишь в пределах 5, причем считают в основном с использо­ванием наглядного счетного материала (пальцы, палочки, клеточки), допуская при этом множество ошибок в вычис­лениях. В отличие от хорошо подготовленных учащихся эти дети, придя в школу, знают не все цифры, недостаточно четко дифференцируют порядковые и количественные числительные. Хуже знают они названия геометрических фигур, часто не понимают пространственные отношения, обо­значенные такими словами, как «вокруг», «после», «между».Дети плохо ориентируются в тетради (не могут правильно найти строчку, начать работу в требуемом месте). Что касается умения решать арифметические задачи, то учащиеся часто допускают ошибки, обусловленные неспособностью сосре­доточиваться на задании, удерживать в памяти числовые данные и вопрос задачи. Ребенок не может представить и самостоятельно проанализировать ту жизненную ситуа­цию, которая описана в задаче. Кроме того, как и при вы­полнении других заданий, дети часто действуют необдуманно, импульсивно, производя поспешные действия с числами.

Таким образом, недобрав к моменту поступления в шко­лу знания и умения, необходимые для обучения математике, дети в дальнейшем испытывают повышенные трудности в усвоении программы. На трудностях в обучении математике не могут не сказываться и такие особенности этих учащихся, как снижен­ная познавательная активность, колебания внимания и ра­ботоспособности, недостаточное развитие основных мыс­лительных операций, некоторое недоразвитие речи. Все эти особенности детей, имеющих некоторое отстава­ние в развитии, вместе с недостаточностью их первоначальных математических знаний и представлений создают повышенные трудности в овладении ими школьными знания­ми по математике. Поскольку состав учащихся каждого класса неоднороден, в нем всегда встречаются дети, кото­рые усваивают материал медленно и не полностью, плохо запоминают и слабо удерживают то, что преподносится на уроке; их знания недостаточно прочны и четки. Всем этим детям требуется дополнительная помощь учителя. Добиться успешного овладения учащимися программным материалом можно при условии использования в преподавании специальных коррекционных приемов, дифференцированного подхода к детям, с учетом особенностей их психического развития.

Коррекционно-развивающая работа с детьми, испытывающими трудности в усвоении математики; строится в соответствии со следующими основными положениями [2; 3; 22]: восполнение пробелов дошкольного математического развития детей путем обогащения чувственного опыта организации предметно-практической деятельности; пропедевтический характер обучения: подбор заданий, подготавливающих учащихся к восприятию новых и трудных тем; дифференцированный подход к детям – с учетом сформированности знаний, умений и навыков, осуществляемый при выделении следующих этапов работы: выполнение действий в материализованной форме, в речевом плане без наглядной опоры, в умственном плане; формирование операции обратимости и связанной с ней гибкости мышления; развитие общеинтеллектуальных умений и навыков – активизация познавательной деятельности: развитие зрительного и слухового восприятия, формирование мыслительных операций; активизация речи детей в единстве с их мышлением; выработка положительной учебной мотивации, формирование интереса к предмету, навыков учебной деятельности, самоконтроля.

Центральное место в программе математики для начальной школы [22] занимает изучение нумерации чисел и арифметических действий с числами. Успешность изучения математики в первом и последующих классах зависит от качества усвоения детьми состава чисел первого десятка.

Многие первоклассники, приступая к обучению, не ус­пели приобрести достаточный наглядно-практический опыт, необходимый для успешного формирования понятия числа. Владея чисто механическим счетом по 1, дети не все­гда могут соотнести числительное с определенным количе­ством реальных предметов. Поэтому в работе с такими уча­щимися, прежде всего, нужно расширить их опыт действий с предметными множествами, уточнив при этом основные математические понятия. На каждом уроке математики они должны как можно больше считать, причем не просто заучивать на память числовой ряд, а учиться сначала пере­считывать именно реальные предметы, окружающие их, а также специальный счетный материал: палочки, кубики, иг­рушки, картинки, геометрические фигуры и др. В ходе таких упражнений следует отрабатывать у каждого ученика умение соотносить при счете называемое числительное с теми конкретными предметами, которые он пересчитывает. В этот же период учащиеся сначала по показу учителя, а за­тем только по его словесной инструкции составляют мно­жества из отдельных предметов, располагают их в определенной последовательности, объединяют и разъединяют группы предметов, учатся сравнивать и уравнивать их разными способами, увеличивать и уменьшать. В процессе предметно-практической деятельности у детей формируются основные математические понятия равенства и неравенства количества предметов («больше на...», «меньше на...», «столько же»), а также понятия чис­ла, арифметических действий сложения и вычитания. Наблюдая за изменением исходного количества, дети приходят к выводу о том, что оно увеличивается, когда предметы приносят, добавляют, и уменьшается, когда их уносят, убирают, отдают и т. п. При этом они усваивают взаимосвязь арифметических действий сложения и вычитания: когда часть предметов перекладывают из одной группы в другую, то в первой количество предметов умень­шается, но одновременно увеличивается количество пред­метов в другой группе. Рассказывая о своих действиях, дети практически усваи­вают ту терминологию, которая встретится им позднее в текстах арифметических задач: «всего», «вместе», «стало», «осталось», «увеличилось», «уменьшилось», «одинаково» и др., что являет­ся подготовкой к пониманию задач разных видов.

В целях закрепления указанных выше математических понятий, а также для развития тонкой моторики для слабо­успевающих учеников нужно увеличивать объем графических работ в тетрадях [22]: обводку шаблонов, раскрашивание, штриховку, рисование по клеточкам несложных фигур и орнаментов. Этой же цели – пропедевтике изучения арифметиче­ских действий и задач разных видов – служат упражнения на различение и выделение предметов и групп предметов. Эти упражнения помогают лучшему усвоению зна­ний по математике, развивают ориентировку в свойствах предметов, помогают расширению пространственных пред­ставлений. Кроме того, они способствуют снятию умствен­ного переутомления, которое часто наступает на уроке у детей с ослабленным здоровьем. Доступная таким учащим­ся предметно-практическая деятельность повышает интерес к занятиям.

Особое внимание нужно уделить отработке у детей уме­ния сравнивать две группы предметов по количеству без пересчитывания, способом взаимно-однозначного соотне­сения. Для этого они располагают сравниваемые предметы один под другим, выделяют пары, находят «лишние» и «недостающие» предметы. Затем дети учатся сравнивать груп­пы предметов, расположенные двумя отдельными «кучка­ми». На этом этапе следует чаще задавать вопросы: «Каких предметов больше?», «Каких предметов меньше?»

Для детей, испытывающих трудности в обучении, такая же предварительная подготовка должна осуществляться систематически при изучении всех основных разделов кур­са начальной математики – путем использования практи­ческих упражнений, направленных на формирование кон­кретных навыков и практических обобщений.

Особенности детей данной категории требуют препод­несения материала небольшими дозами, с более постепен­ным, чем обычно, усложнением. Чтобы прийти к нужному выводу, обобщению, для некоторых учащихся требуется выполнение большого количест­ва упражнений. Если для хорошо успевающих учеников бывает достаточно разобрать какое-либо правило, пример, показать прием вычислений, то отдельным учащимся нуж­ны многократные разнообразные упражнения с использо­ванием различных форм наглядности.

Центральной задачей обучения математике в начальной школе является выработка полноценных вычислительных навыков. Результаты табличного сложения (вычитания) и умножения (деления) дети должны знать наизусть. Следует обратить внимание на то, что учащиеся со слабой математической подготовкой часто пытаются просто выучить таблицы, не всегда осознавая взаимосвязь арифметических действий, не умея использовать те приемы, которые облег­чили бы им вычисления. Сознательному усвоению таблич­ных значений будут способствовать описанные вы­ше действия.

При изучении нумерации чисел первого десятка важно добиться, чтобы все ученики научились уверенно вести счет не только в прямом, но и в обратном порядке, а также начиная с любого числа числового ряда и заканчивая на заданном числе. Для этого они должны понять общий прин­цип построения натурального ряда, т. е. что каждое число можно получить путем прибавления единицы к предыду­щему числу или вычитания единицы из числа, следующего при счете за данным. В помощь детям, которые плохо запоминают последовательность числительных, можно предложить индивидуальную карточку с записанным на ней числовым рядом (сначала до 10, потом до 20) или обычную ученическую линейку с сантиметровой шкалой. С помо­щью такой зрительной и тактильной опоры слабоуспеваю­щим учащимся будет легче выполнять разнообразные задания: показывать предыдущее и последующее число, находить соседей числа и число по его соседям, сравнивать числа, запоминать состав чисел первого десятка. При этом развернутые внешние действия постепенно заменяются сокращенными, а затем становятся автоматизированными. Например, переставляя пальцы по числовому ряду вправо и влево, а затем без помощи пальцев, опираясь на числовой ряд глазами и, наконец, мысленно вспоминая последовательность чисел, учащиеся овладевают присчитыванием и отсчитыванием по одной единице, потом по 2, 3. При этом рассуждения детей также сокращаются, переходя от полностью развернутых во внутренний план. В случае затруднений следует снова вернуться к подробным объяснениям и развернутым внешним действиям. Например, прибавляя число 3 с опорой на числовой ряд, учащиеся сначала рассказывают о том, как присчитывают 1,1 и еще 1, фиксируя пальцами исходное число, промежуточный результат и конечный итог. Через некоторое время дети начинают считать про себя, не фиксируя промежуточный результат, а называя только конечный. И, наконец, дети перестают фиксировать цифры пальцами, начиная считать «в уме».

При изучении состава чисел первого десятка отдельным ученикам также требуется увеличение количества тренировочных упражнений. Вначале всевозможные варианты состава чисел демонстрирует учитель. Затем сами учащиеся, расчленяя множество предметов на две подгруппы и со­ставляя вновь одно множество, убеждаются, что при всех вариантах в результате получается то же число.

Для лучшего запоминания состава чисел целесообразно увеличить количество графических работ учащихся в тетрадях.

Процесс запоминания таблиц должен быть осознанным, что должно выражаться в умении детей показывать и объяснять состав любого числа на конкретном счетном материале, использовать знания приемов вычислений при решении задач и примеров. В случае затруднений в счете детей необходимо опять возвращать к упражнениям на наглядном материале. Решая пример, ученик должен подробно рассказывать, как он производил те или иные вычисления, какими приемами пользовался, что получил в результате. У слабоуспевающих учащихся важно воспитать осознанность своих действий, а также навыки самоконтроля [13; 22]. Поэтому решение примеров надо подробно комментировать и сопровождать заданиями, связанными с практической деятельностью ребенка.

Для лучшего осмысления учащимися взаимосвязи ариф­метических действий сложения и вычитания, а позднее ум­ножения и деления целесообразно чаще предлагать им та­кие задания.

– По данному примеру составьте еще один пример на сложение (умножение) и два примера на вычитание (деле­ние).

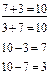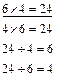Для детей со слабым логическим мышлением это же за­дание может быть индивидуальным и несколько облегченным.

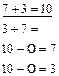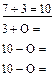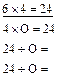Решение и сопоставление таких примеров не только способствует запоминанию таблиц, но также играет корригирующую роль, помогая развитию обратимых мыслительных операций.

Для лучшего понимания взаимообратности арифметических действий можно использовать обобщенную форму записи.

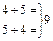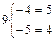Из-за недостатков памяти некоторые дети плохо запоминают названия компонентов арифметических действий, часто смешивают эти названия. Учителю рекомендуется [2; 20; 22] пользоваться в своей речи соответствующей терминологией, постепенно побуждая к этому учащихся. Для лучшего усвоения математической терминологии отдельным, наиболее слабо успевающим детям на некото­рое время можно разрешить пользоваться индивидуальной карточкой-памяткой, в которой записан соответствующий пример с названиями компонентов.

У учеников, только что приступивших к обучению в школе, довольно часто встречаются отклонения в развитии моторной сферы, что создает определенные трудности при написании цифр, измерении. Для развития тонкой моторики кистей и пальцев рук с этими детьми рекомендуется ежедневно проводить пальцевую гимнастику, а также организовывать дополнительные упражнения, под­готавливающие руку к письму: рисование радуги, клубов дыма, чешуек рыб, дорисовывание недостающих деталей у предметов, обводка лекал, заштриховывание и раскрашивание [20]. Отдельным учащимся можно предлагать индивидуальные задания, укрепляющие мышцы пальцев рук: разминать пластилин и глину, запускать пальцами небольшие волчки, катать по очереди каждым пальцем мелкие бусины, шарики, перебирать крупу, заводить ключиком механические игрушки, нанизывать пуговицы и др. У некоторых учеников вызывает трудности запоминание цифр. Для них нужно предусмотреть дополнительную коррекционную работу: лепку цифр из пластилина, ощупывание цифр, изготовленных из разного материала. В процессе знакомства с изучаемой цифрой после показа учителем написания цифры на доске учащиеся обводят указкой модели цифр, пишут их в воздухе, на доске, а затем в тетрадях. Для отдельных учеников требуется обводка цифр по пунктиру, тонким линиям, по нескольким опорным точкам. Если ученик затрудняется писать в одну клеточку, ему не­которое время разрешается писать в тетради с более круп­ной клеткой или в обычной тетради, но в две клеточки.

Некоторые дети долгое время не могут усвоить алгоритм рассуждений и овладеть рядом последовательных дейст­вий. Например, при решении примеров на сложение и вычитание с переходом через десяток нужно сначала разло­жить число на два слагаемых, затем добавить до десятка и прибавить второе слагаемое. Поскольку некоторым уча­щимся трудно удержать в памяти все числа, им можно разрешить записывать промежуточные результаты.

Многие школьники при нахождении суммы или разности чисел рисуют палочки, точки и пересчитыва­ют их (зачеркивают) для получения результата. Нужно вовремя перевести их с этого нерационального приема пересчитывания на более совершенный и удобный прием присчитывания. При этом следует постепенно увеличивать дозу трудностей: предлагать сначала присчитывать и отсчитывать по одной единице, затем по две, по три и т.д. Наиболее слабым учащимся можно разрешить пользоваться в качестве зрительной опоры записанным числовым рядом или шкалой линейки.

Для того чтобы сделать вычислительные приемы более наглядными и понятными для учеников, можно рекомендовать использовать различные опорные сигналы: дуги, лучи, рамки и др. Образцы некоторых опорных сигналов есть вучебниках математики. Например, при изучении сложе­ния и вычитания в пределах 20 удобно пользоваться опорным сигналом «рамка».

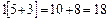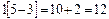Эта же запись может быть и менее развернутой.

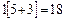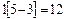При объяснении темы «Сложение и вычитание с перехо­дом через десяток» можно рекомендовать учащимся использовать другие опорные сигналы – «лучи», причем несколько более наглядно, чем это предложено в учебнике 1 класса.

Вот развернутая запись примера для слабых учеников.

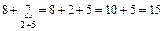
Сокращенная запись.

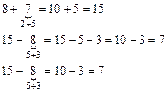
При решении примеров на сложение и вычитание двузначных чисел учащиеся могут пользоваться опорным сигналом – «дуга»:

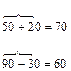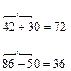Каждый раз дети должны сопровождать записи подробным комментированием, рассказывая о том, как они считали.

Аналогичные опорные сигналы можно использовать при изучении действий умножения и деления. Применение опорных сигналов облегчает детям усвоение приемов вычисления и позволяет им чувствовать себя более уверенными на уроке.

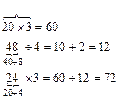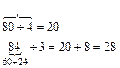Для лучшего усвоения того или иного вычислительного приема учащимся могут быть предложены индивидуальные задания с наличием развернутого образца способа вычисления. Соотнося свои действия с образцом, ученики постепенно усваивают вычислительные приемы. Например. Выполни действия по образцу:

86 : 2 = (80 + 6) : 2 = 80 : 2 + 6 : 2 = 40 + 3 = 43.

Затем этот развернутый образец способа вычислений заменяется сокращенным: 86 : 2 = (80 + 6) : 2 = 43.

И, наконец, задание выполняется без наличия образца полностью самостоятельно.

Некоторые дети долгое время не могут запомнить таблицу умножения однозначных чисел и соответствующие случаи деления. Нужно показать таким учащимся приемы запоминания таблиц [20]. Для закрепления знания таблиц следует чаще включать их повторение, а также увеличивать количество тренировочных упражнений для слабоуспевающих учащихся. Но в классе всегда найдутся такие ученики, которым учитель бу­дет вынужден разрешить еще некоторое время заглядывать в таблицу умножения, напечатанную на обложке тетради. Не следует при этом заставлять детей просто механически заучивать таблицы – они должны уметь объяснить каждый случай умножения и деления, проиллюстрировать его на конкретных предметах, заменить умножение суммой одинаковых слагаемых, сделать рисунок к примеру и т. д.

Учитывая индивидуальные возможности учащихся, на каждом этапе урока учителю следует предусматривать задания различной степени трудности. Если при знакомстве с новым материалом большинство учеников могут самостоятельно выполнить аналогичное задание, то дети с отставанием в развитии справляются с ним только под контролем и с помощью учителя. Требуются также дополнительные вопросы и разъяснения, применение наглядности. Например, при закреплении навыков образования какого-либо числа одни дети решают примеры на сложение, другие рисуют или обводят клеточки в тетрадях, а наиболее неподготовленные только раскрашивают нарисованные учителем образцы.

При составлении самостоятельных работ учитель также должен предусмотреть различные по трудности индивидуальные задания [22]. Все учащиеся одновременно выполняют одну и ту же работу, но если кто-то может справиться с ней полностью самостоятельно, то другим требуется помощь, а третьи успеют выполнить еще и дополнительное задание. Например, нужно составить задачу по рисунку на доске (изображены 2 ящика с яблоками, под одним записано 14 кг, под другим – 2 кг). Все дети записывают вопросы и решения составленных задач. При этом сильные ученики могут составить по рисунку пять задач. Слабо подготовленным детям можно предложить различные виды помощи. Например:

– Поставьте вопрос так, чтобы задача решалась вычитанием (сложением).

– Поставьте вопрос к задаче, используя слова «на сколько больше…».

– Поставьте вопрос со словами «во сколько раз меньше…».

Можно предложить всем детям решать задачу по учебнику, при этом сильным – составить к ней две обратные задачи, а наиболее слабо подготовленным к анализу условия дать вспомогательные вопросы типа «Как найти скорость, если известны время и расстояние?». В некоторых случаях есть необходимость предоставлять ученику готовый план решения задачи. Дифференцированный подход нужно осуществлять и при формировании вычислительных навыков.

Переходя от выполнения задания под непосредственным руководством учителя к частично самостоятельной работе и далее к полностью самостоятельной работе, ученики последовательно справляются с заданиями разной степени трудности. При этом трудность задания и степень самостоятельности постепенно нарастают, что способствует реализации дидактического принципа «от простого к сложному».

Известно, что для детей, испытывающих трудности в обучении, характерны неравномерность, нецеленаправленность деятельности. Обычно на уроках математики, как и на других уроках, они неорганизованны, импульсивны, склонны к поспешным, необдуманным действиям. Эффективным приемом для нормализации учебной деятельности младших школьников является алгоритмизация. С его помощью осуществляются подчинение ребенка какому-либо предписанию, перенос алгоритма решений на такие задачи, условия которых внешне не сходны с условиями предыдущих задач, а также обобщение операций, систематизация знаний. Это различные памятки-инструкции, в которых записана последовательность действий при решении уравнений, задач, трудных случаев умножения и деления и др. Использование данного приема позволяет [22] осуществлять коррекцию недостатков памяти слабоуспевающих учащихся, так как при работе по алгоритмам происходит их заучивание и автоматизация, а также коррекция недостатков мышления, поскольку происходит обобщение действий и операций. Проговаривая и выполняя инструкцию по отдельным этапам, дети учатся правильно рассуждать и контролировать себя в процессе самостоятельной работы.

Такие же памятки можно предложить во время выполнения самостоятельной работы ученикам, которые не усвоили то или иное умение.

Приемам пользования отдельными дидактическими пособиями, памятками, схемами, алгоритмами действий следует обучать на индивидуальных коррекционных занятиях [13]. При этом учитель имеет возможность проверить правильность рассуждений ученика, понять, почему и в чем он ошибся, какое звено рассуждений опустил. Индивидуаль­ные разъяснения учителя и дополнительные тренировочные упражнения с подробными объяснениями каждого эта­па работы помогут детям избежать ошибок в само­стоятельной работе.

Решение арифметических задач, как известно, является одним из самых трудных разделов программы по математике. От ребенка требуется осуществление довольно сложной аналитико-синтетической деятельности: с одной стороны, он должен уметь наглядно представить описанную в задаче жизненную ситуацию, с другой – уметь отвлечься от конкретной ситуации и перевести ее в арифметический план, записав решение в виде примера. Младшие школьники часто не знают, в какой последовательности нужно работать над задачей. Их приходится учить, с чего начинать, как анализировать текст задачи, как устанавливать связь данных и искомого, чем заканчивать решение, как формулировать ответ, т. е. формировать умение мысленно составлять план работы над любой задачей. Для этого полезно приучать детей пользоваться памяткой следующего типа [22].

1. Внимательно прочитай задачу два раза.

2. Подумай, что в задаче известно.

3. Что спрашивается в задаче? Запиши задачу кратко.

4. Рассмотри краткую запись задачи и подумай, как найти неизвестное.

5. Реши задачу. Объясни решение.

6. Проверь правильность решения.

Сначала такую памятку можно вывесить в виде плаката для фронтальной работы в классе, а затем составить индивидуальные памятки. Для учеников, которые усвоили последовательность работы над задачей, можно опускать некоторые звенья и постепенно свертывать рассуждения. Некоторым же учащимся придется пользоваться такими памятками более длительное время.

Стойкие затруднения у слабоуспевающих младших школьников вызывает решение составных арифметических задач. Здесь требуется умение выстраивать цепочку рассуждений, чтобы ответить на главный вопрос задачи. При этом учащиеся делают множество разнообразных ошибок [20]: опускают промежуточное действие, неверно составляют краткую запись задачи, не могут пояснить даже правильно выполненное решение, смешивают задачи разных видов, теряют числовые данные и др. Учитель должен особое внимание уделить этапу пропедевтики. Продумывая методику изучения какой-либо составной задачи, педагог вычленяет в ней наиболее трудное звено и предварительно проводит упражнения, которые подготавливают учащихся к восприятию. Например, если в составную задачу входит простая задача на разностное или кратное сравнение, то перед ее решением следует потренировать детей в решении задач данного вида в одно действие. В этот же период следует уточнить понимание терминов, необходимых для усвоения содержания составных задач (цена, количество, стоимость скорость, время, расстояние и др.).

Можно рекомендовать [22] следующие задания, непосредственно направленные на подготовку детей к пониманию задач в два действия: постановка вопроса к данному условию; подбор числовых данных к вопросу; решение задач с недостающими данными; решение задач-вопросов без числовых данных, требующих одних лишь рассуждений; составление задачи по данному решению; выполнение упражнений, помогающих осмыслить математические выражения, составленные по задаче; решение цепочек простых задач, из которых вторая задача является продолжением первой.

В процессе выполнения этих заданий следует предлагать детям вопросы: «Можем ли мы сразу ответить на вопрос задачи?», «Что нужно знать, чтобы ответить на вопрос задачи?» При этом ребенок приучается рассуждать, формулировать свои мысли, доказывать, что служит хорошей пропедевтикой к анализу составных задач.

Только после такой подготовительной работы, когда все ученики научатся подбирать числовые данные к вопросу и вопросы к числовым данным, будут легко решать цепочки простыx задач разных видов, можно приступать к ознакомлению детей с составными арифметическими задачами. На каждом этапе работы над этими задачами следует преду­сматривать индивидуальную помощь детям с недостаточной математической подготовкой [2; 20; 22] . Например, учитывая тот факт, что многие дети читают текст задачи невнимательно, не вдумываясь в содержание, следует приучать их прочитывать задачу дважды. Нужно настроить учащихся на то, что они, прежде всего, должны мысленно представить себе, о чем рассказывается в задаче, чтобы понять, что происходит с величинами. Нужно постараться ввести каждого ученика в задачу как действующее лицо. Пусть каждый ребенок представит себе, что это он едет в лодке и т.п.

Все слова, содержащиеся в тексте задачи, должны быть понятны ученикам. Для детей, имеющих недостаточный жизненный опыт и ограниченный словарный запас, требуется разъяснение некоторых слов и выражений, встречающихся в учебнике математики для начальной школы («дистанция», «автопробег», «разделиться на бригады», «работать с одинаковой производительностью труда» и др.). Учителю нужно предусмотреть предварительную работу по разъяснению и уточнению малопонятных для некоторых детей словосочетаний, для того чтобы у них не возникло неверное представление о содержании задачи. Особенно это касается тех слов, которые помогают уяснить зависимости величин: «поровну», «в каждом», «одновременно» и др. Для пояснения некоторых ситуаций следует использовать наглядную демонстрацию определенных действий (в задачах на движение), а также рисунки, чертежи.

В работе над словами, влияющими на выбор арифметического действия, следует показать детям, что и в составных задачах, и в простых одно отдельно взятое слово еще не определяет выбор действия – для этого нужен внимательный и всесторонний анализ жизненной ситуации, описанной в задаче.

Главная цель учителя – научить каждого ученика самостоятельно решать арифметические задачи. У младших школьников наблюдаются заметные индивидуальные различия в овладении этим умением. Одни дети более yспешно справляются с задачами какого-либо вида. Другим требуется увеличение числа подготовительных упражнений. Часть детей нуждается в более подробном развертывании какого-либо этапа работы над задачей. Некоторым детям необходимо больше тренировочных упражнений для того, чтобы подвести их к нужному обобщению. Поэтому в процессе обучения следует применять дифференцированный подход к детям.

В зависимости от темы и целей каждого отдельного урока математики учитель вправе подбирать самые разные методы преподнесения материала. Но в работе с детьми, имеющими недостаточную математическую подготовку, предпочтение следует отдавать коррекционным методам, которые способствуют развитию познавательной активно­сти этих учащихся, их мышления и речи. Дифференцированные задания с учетом особенностей слабоуспевающих детей помогут им преодолеть недостатки своего развития, восполнить пробелы в дошкольных математических знаниях и заложат основу для дальнейшего изучения курса математики в школе.