Алгоритм №2 вычисления ранга матрицы
(метод элементарных преобразований).
1. С помощью элементарных преобразований получить а11=1.
2. С помощью элементарных преобразований получить аi1=0, i¹1 ( все элементы первого столбца, кроме первого, равны 0).
3. Выполнить пункты 1 и 2 алгоритма для элементов второго столбца.
4. продолжать алгоритм до тех пор, пока матрица не будет приведена к ступенчатому виду:
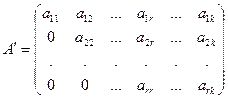 .
.
5. Ранг полученной ступенчатой матрицы А¢ будет равен рангу исходной матрицы. rangA = rangA¢ = 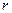 .
.
Строки (столбцы) матрицы 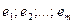 называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа 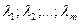 не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:
не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке: 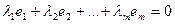 , где
, где 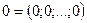 . В противном случае строки матрицы называются линейно независимыми.
. В противном случае строки матрицы называются линейно независимыми.
Пример выполнения заданий практической части
Пример 1. Найти методом окаймления миноров ранг матрицы
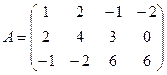 .
.
Решение. Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) М1 = 1, расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор
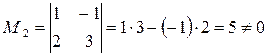 .
.
Переходим теперь к минорам 3-го порядка, окаймляющим М2. Их всего два (можно
добавить второй столбец или четвертый). Вычисляем их:
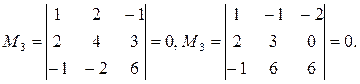
Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум: 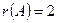 .
.
Пример 2. Найти ранг матрицы с помощью элементарных преобразований:
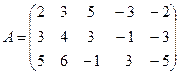 .
.
Решение. Из второй строки вычтем первую и переставим эти строки
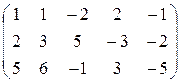 .
.
Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:
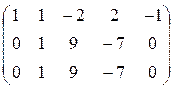 ;
;
из третьей строки вычтем первую, получим матрицу
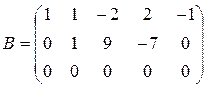 ,
,
которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2.
Пример 3.Выяснить, при каком значении параметра 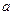 матрица имеет 3 линейно независимые строки:
матрица имеет 3 линейно независимые строки: 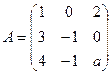 .
.
Решение. Матрица 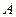 имеет три линейно независимые строки, если ее ранг равен 3, т.е.
имеет три линейно независимые строки, если ее ранг равен 3, т.е. 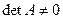 . Вычислим определитель матрицы:
. Вычислим определитель матрицы:
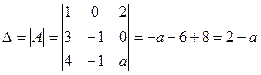 ,
,
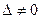 , т.е.
, т.е. 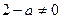 ;
; 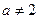 .
.
Следовательно, при всех значениях 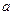 , кроме
, кроме 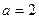 , все строки линейно независимы.
, все строки линейно независимы.
Пример 4. Определить максимальное число линейно независимых строк (столбцов) матрицы: 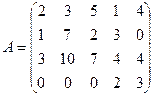 .
.
Решение. С помощью элементарных преобразований, не меняющих ранга матрицы, приведем ее к ступенчатому виду:
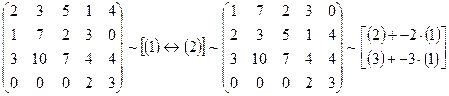 ~
~ 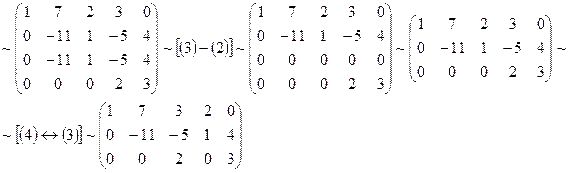
Значит, ранг матрицы 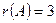 и исходная матрица имеет 3 линейно независимые строки (или столбца).
и исходная матрица имеет 3 линейно независимые строки (или столбца).
Задания для аудиторного занятия
1. Найти методом окаймления миноров ранг матрицы:
1.1. 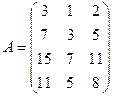 ; 1.2.
; 1.2. 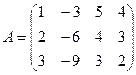 ;
;
1.3. 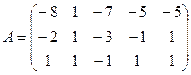 ; 1.4.
; 1.4. 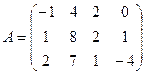 .
.
2.Найти ранг матрицы с помощью элементарных преобразований:
2.1. 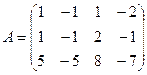 ; 2.2.
; 2.2. 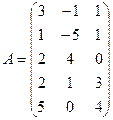 ;
;
2.3. 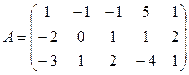 ; 2.4.
; 2.4. 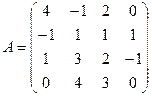 ;
;
2.5. 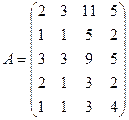 ; 2.6.
; 2.6. 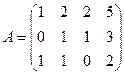 .
.
3.Найти максимальное число линейно независимых строк матриц:
3.1. 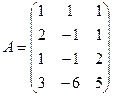 ; 3.2.
; 3.2. 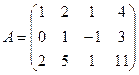 ;
;
3.3. 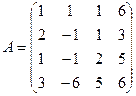 ; 3.4.
; 3.4. 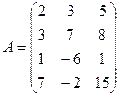 .
.
Домашнее задание
1.Найти методом окаймления миноров ранг матрицы:
1.1. 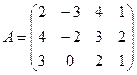 ; 1.2.
; 1.2. 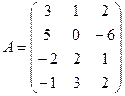 ;
;
1.3. 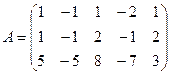 .
.
2. Найти ранг матрицы с помощью элементарных преобразований:
2.1. 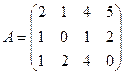 ; 2.2.
; 2.2. 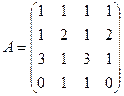 ;
;
2.3. 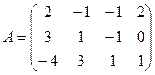 .
.
3.Найти максимальное число линейно независимых столбцов матриц:
3.1. 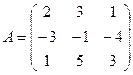 ; 3.2.
; 3.2. 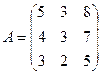 .
.
