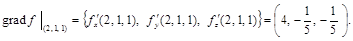Производная сложной и неявной функции

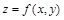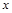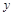Пусть – функция двух переменных и , каждая из которых является функцией независимой переменной 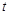: 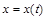, 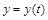. В этом случае функция 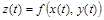является сложной функцией одной независимой переменной 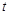; переменные 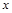и 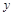– промежуточные переменные.

Теорема 1. Если 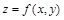дифференцируемая в точке 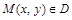функция и 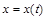, 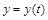– дифференцируемые функции независимой переменной 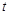, то производная сложной функции 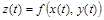вычисляется по формуле

.

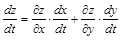Пример 1.Найти 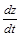, если

.

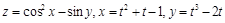Решение. Функция 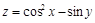, как функция переменных х, у, дифференцирована во всей плоскости Оху, поскольку имеет частные производные

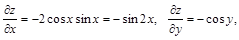
непрерывные в произвольной точке .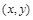

Функции 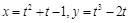дифференцированы на всей числовой прямой 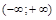, так как производные

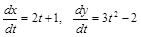
существуют для любого .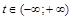

Таким образом, для функции 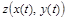выполняются все условия теоремы. Поэтому для произвольного 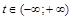по формуле имеем:

.

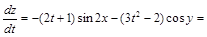
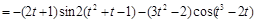Если функция задана неявно уравнением 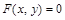, то производную неявной функции вычисляют по формуле

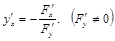
Если функция 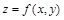задана уравнением 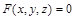, неразрешенным относительн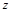о , то

.

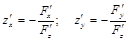Пример 2.Найти частные производные функции 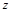, заданной уравнением .

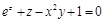Решение. Имеем:

.

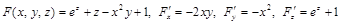Итак, по формуле

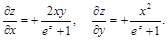
Пример 3.Найти 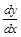, если неявная функция 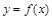задана уравнением .

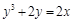Решение.

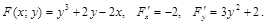
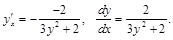
Использование частных производных в геометрии

Касательная плоскость и нормаль к поверхности

Пусть задана поверхность 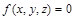, точка 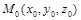принадлежит этой поверхности и функция 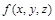дифференцирована в точке .

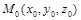Уравнение касательной плоскости к заданной поверхности в точке 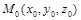имеет вид

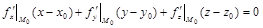, (1)

уравнение нормали –

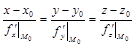. (2)

Порядок нахождения уравнений касательной плоскости и нормали к поверхности:

1. вычисляем частные производные 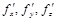в точке ;

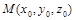2.подставляем найденные значения у уравнения (1), (2).

Если задано только значение 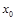и 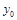, то координата 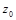точки 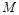определяется из условия, что точка М принадлежит заданной поверхности, т.е. .

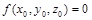Если поверхность задана уравнением 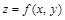, то уравнение нормали и касательной плоскости имеют вид:

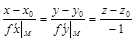; (3)

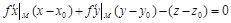. (4)

Пример 1.Найти уравнение касательной плоскости и нормали к поверхности 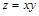в точке .

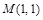Решение.

Запишем уравнение поверхности в виде 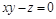, т.е.

.

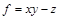Координаты точки М: 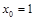, 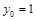. Координата 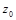определяется из условия, что точка М принадлежит заданной поверхности, т.е. 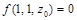. Имеем .

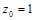Вычислим частные производные 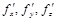в точке :

.

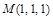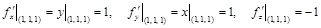Воспользуемся уравнением (1) и (2). Имеем уравнение касательной плоскости

;

.

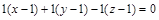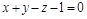Уравнение нормали

;

.

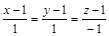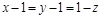Определение 1. Градиент функции 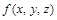в точке 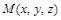— это вектор, координатами которого являются значения частных производных функции 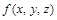в точке :

,

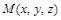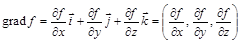где 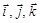— единичные векторы (орты).

Пример 2.Найти градиент функции 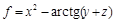в точке .

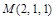Решение.Найдем частные производные функции :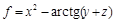

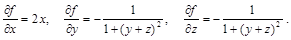
Вычислим частные производные функции 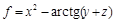в точке :

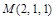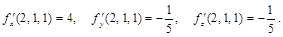
Вычислим градиент функции 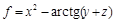в точке :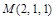