Упражнения к разделу 3.4
Найти частные производные функции:
1. 
. Найти 
.
2. 
. Найти . 
3. 
. Найти 
.
Найти полный дифференциал функции:
4. 
.Найти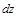 
. 
5. 
.Найти .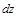 
6. 
.Найти .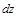 
Вычислить приближенно:
7. 
. 
8. 
. 
Найти частные производные первого и второго порядка функций:
9. 
.
10. 
.
11. 
.
12. 
.
Найти стационарные точки функций, и исследовать их характер:
13. 
. 
—стационарная точка и точка минимума, 
14. 
. —стационарная точка, в точке 
экстремума нет 
15. 
. 
—стационарная точка, 
—точка минимума, 
16. 
. 
—стационарная точка. 
—точка минимума, 
Найти производные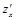 
, 
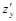функции 
, где
.
17. 
.
18. 
.
19. 
.
Найти производные функций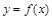 
, заданных неявно уравнениями.
20. 
. 
21. 
. 
Найти градиент функции 
в точке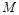 
.
22. 
. 
23. 
24. 
25. 
26. 
Найти уравнение касательной плоскости и нормали к поверхности в точке :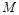
27. 
.
28. 
.
29. 
.
30. 
.
31. 
.
Задания для индивидуальной семестровой работы студентов к разделу 3.4
1.а) найти ;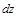
б) найти приближенное значение функции 
в точке 
;
в) написать уравнение касательной плоскости и нормали к поверхности в точке 
, если 
задано:
1). 
, 
2). 
, 
.
3). 
, 
4). 
, 
5). 
, 
6). 
, 
.
7). 
, 
.
8). 
, 
.
9). 
, 
.
10). 
, 
.
11). 
, 
.
12). 
, 
.
13). 
, 
.
14). 
, 
.
15). 
, 
.
16). 
, 
.
17). 
, 
.
18). 
, 
.
19). 
, 
.
20). 
, 
21). 
, 
.
22). 
, 
.
23). 
, 
.
24). 
, 
.
25). 
, 
.
26). 
, 
.
27). 
, 
.
28). 
, .
29). 
, 
.
30). , 
.
2.Задана дифференцированная функция 
, где 
, 
. Найти производную 
.
1). 
.
2). 
.
3). 
.
4). 
.
5). 
.
6). 
.
7). 
.
8). 
.
9). 
.
10). 
.
11). 
.
12). 
.
13). 
.
14). 
.
15). 
.
16). 
.
17). 
.
18). 
.
19). 
.
20). 
.
21). 
.
22). 
.
23). 
.
24). 
.
25). 
.
26). 
.
27). 
.
28). 
.
29). 
.
30). 
.
3. Исследовать на экстремум функцию :
1). 
.
2). 
.
3). 
.
4). 
.
5). 
.
6). 
.
7). 
.
8). 
;
9). 
.
10). 
.
11). 
.
12). 
.
13). 
.
14). 
.
15). 
.
16). 
.
17). 
.
18). 
.
19). 
.
20). 
.
21). 
.
22). 
.
23). 
.
24). 
.
25). 
.
26). 
.
27). 
.
28). 
.
29). 
.
30). 
.
Глава 4 ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Неопределенный интеграл
Первообразная и неопределенный интеграл
Определение 1.Функция 
называется первообразной функции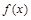 
на некотором промежутке Х, если для любого 
функция 
дифференцируема и выполняется равенство:
(1)
Например, функция 
есть первообразной функции 
на 
, т.к. 
Определение 2.Совокупность всех первообразных функций для функции 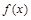на промежутке Х называется неопределенным интегралом от функции 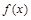на этом промежутке и обозначается
, т.е. 
, (2)
где – какая-нибудь первообразная функции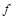 
на промежутке, который рассматривается; С – произвольная постоянная.
В выражениях (2) и (3) функция 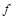называется подинтег-ральной функцией, 
– подинтегральным выражением.
Операция нахождения неопределенного интеграла функции называется ее интегрированием. Переменная х называется переменной интегрирования.
Например, 
, поскольку для произвольного фиксированного С имеем 
.
Если F — какая-нибудь первообразная функции f на промежутке Х, и согласно формуле (3) под знаком интеграла является дифференциалом функции F: 
. Будем считать по определению, что этот дифференциал под знаком интеграла можно записывать в любом из указанных видов, т.е.
. (3)
Если построить кривую – график одной первообразной функции , то все другие кривые (графики других первообразных для одной функции) получают путем смещения этой кривой по оси 
на величину, которая равняется значению постоянной С.
 |