Упражнения к разделам 4.2 и 4.3
Вычислить интегралы, пользуясь подстановками:
1). 
2). 
3). 
4). 
5). 
6). 
Вычислить интегралы интегрированием по частям:
7). 
8). 
9). 
10). 
Вычислить несобственные интегралы и исследовать на сходимость:
11). 
[расходящийся]
12). 
. [расходящийся]
13). 
[расходящийся]
14). 
. 
15). 
[расходящийся]
Найти площадь фигуры, ограниченной графиками функций:
16). 
17). 
18). 
19). 
Найти площади фигур, ограниченных линиями:
20). 
(кардиоида). 
21). 
22). 
, 
, (астроида). 
Вычислить длину дуги кривой, заданной параметрически:
23). 
24). 
25). 
26). 
27). 
Вычислить объем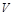 
тела, которое образовывается вращением вокруг оси 
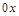фигуры, ограниченной линиями:
28). 
29). 
30). 
31). 
32). 
Известны законы изменения скорости затрат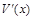 
и дохода 
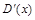, где время t измеряется годами, затраты 
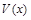и доход 
измеряются млн. грн. За какое время предприятие получит максимальный доход и какой будет величина этого дохода?
33). 
[9 лет, 36млн. грн.]
34). 
[8 лет, 16млн. грн.]
Задания для индивидуальной семестровой работы студентов к разделам 4.2 и 4.3
1Вычислить площадь:
1 
; 
.
2 
; 
.
3 
; 
.
4 
; 
.
5 
; 
.
6 
; 
.
7 
; 
.
8 
; 
.
9 
; 
.
10 
; 
.
11 
; 
.
12 
; 
.
13 
; 
.
14 
; 
.
15 
; 
.
16 
; 
.
17 
; 
.
18 
; 
.
19 
; 
.
20 
; 
.
21 
; 
.
22 
; 
.
23 
; 
.
24 
; 
.
25 
; 
.
26 
; 
.
27 
; 
.
28 
; 
.
29 
; 
.
30 
; .
2 Вычислить объем тел вращения и длины дуг:
1 
; 
.
2 
;
.
3 
; 
.
4 
;
.
5 
; 
.
6 
; 
.
7 
; 
.
8 
;
.
9 
; 
.
10 
;
.
11 
; 
.
12 
;
.
13 
;
.
14 
; 
.
15 
; 
.
16 
;
.
17 
; 
.
18 
; 
.
19 
;
.
20 
; 
.
21 
; 
.
22 
;
.
23 
;
.
24 
; 
.
25 
; 
.
26 
;
.
27 
; 
.
28 
; 
.
29 
; 
.
30 
; 
.
3 Вычислить несобственные интегралы:
1. 
2. 
3. 
.
4. 
5. 
6. 
.
7. 
8. 
9. 
.
10. 
11. 
12. 
.
13. 
14. 
15. 
.
16. 
17. 
18. 
.
19. 
20. 
21. 
.
22. 
23. 
2 24. 
.
25. 
26. 
27. 
.
28. 
29. 
30. 
.
4 Найти дисконтную прибыль за Т лет при 
ставке, если базовые капиталовложения а , а ожидаемая прибыль b годовых:
1 Т = 2; Р = 10 %; b = 1; а = 10.
2 Т = 3; Р = 8 %; b = 1; а = 10.
3 Т = 5; Р = 10 %; b = 2; а = 10.
4 Т = 4; Р = 10 %; b = 2; а = 0.
5 Т = 3; Р = 8 %; b = 1; а = 20.
6 Т = 4; Р = 7 %; b = 3; а = 10.
7 Т = 4; Р = 5 %; b = 3; а = 10.
8 Т = 4; Р = 6 %; b = 3; а = 0.
9 Т = 4; Р = 3 %; b = 1; а = 10.
10 Т = 5; Р = 8 %; b = 2; а = 10.
11 Т = 5; Р = 8 %; b = 2; а = 20.
12 Т = 5; Р = 4 %; b = 4; а = 40.
13 Т = 5; Р = 7 %; b = 4; а = 40.
14 Т = 5; Р = 6 %; b = 4; а = 40.
15 Т = 5; Р = 3 %; b = 4; а = 40.
16 Т = 5; Р = 5 %; b = 3; а = 30.
17 Т = 5; Р = 6 %; b = 1; а = 30.
18 Т = 6; Р = 2 %; b = 2; а = 40.
19 Т = 10; Р = 10 %; b = 10; а = 100.
20 Т = 5; Р = 8 %; b = 1; а = 50.
21 Т = 4; Р = 8 %; b = 5; а = 100.
22 Т = 4; Р = 5 %; b = 10; а = 200.
23 Т = 4; Р = 10 %; b = 2; а = 100.
24 Т = 10; Р = 10 %; b = 0,5; а = 50.
25 Т = 6; Р = 5 %; b = 1; а = 50.
26 Т = 6; Р = 5 %; b = 2; а = 40.
27 Т = 6; Р = 5 %; b = 1; а = 20.
28 Т = 6; Р = 8 %; b = 2; а = 20.
29 Т = 6; Р = 10 %; b = 4; а = 10.
30 Т = 6; Р = 8 %; b = 1; а = 100.
Глава 5 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Основные понятия
Определение 1. Дифференциальным уравнением называется уравнение, связывающее независимую переменную, неизвестную функцию и ее производные (или ее дифференциалы).
Дифференциальное уравнение называется обыкновенным в случае, когда неизвестная функция, входящая в дифференциальное уравнение, зависит только от одной независимой переменной.
Определение 2. Порядком дифференциального уравнения называется наивысший порядок производной (или дифференциала), входящей в уравнение.
Обыкновенное дифференциальное уравнение порядка п в самом общем случае содержит независимую переменную, неизвестную функцию и ее производные или дифференциалы до порядка п включительно и имеет вид
. (1)
В этом уравнении х – независимая переменная, у – неизвестная функция, а 
– производные неизвестной функции.
Определение 3. Обыкновенное дифференциальное уравне-ние первого порядка имеет вид
, (2)
а если его удастся решить относительно производной, то оно запишется так:
. (3)
Задача состоит в определении из дифференциального уравнения неизвестной функции, а процесс определения этой функции называется решением, или интегрированием дифференциального уравнения.
Определение 4. Решением, или интегралом уравнения (2) называется всякая дифференцируемая функция 
, удовлетворяющая этому уравнению, т. е. такая, после подстановки которой в уравнение (2) оно обращается в тождество, т. е.
.
Определение 5. Кривая , определяемая решением уравнения (2), называется интегральной кривой дифференциального уравнения.
Определение 6. Общим решением дифференциального уравнения (2) называются соотношения вида
или 
, (4)
включающие одну произвольную постоянную величину и обладающие тем свойством, что решая их относительно у при любых частных значениях произвольной постоянной, получаем функции вида , являющиеся решениями уравнения (2) или (3).
Уравнения (4) определяют семейство интегральных кривых уравнения (2).
Определение 7. Частным решением дифференциального уравнения (2) называется такое решение, которое получается из общего решения (4) при некотором частном значении произвольной постоянной. Произвольная постоянная С, входящая в (4), определяется из так называемых начальных условий.
Задача с начальными условиями ставится так: найти решение уравнения (2) такое, чтобы оно принимало заданное значение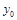 
при заданном значении независимой переменной 
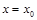, т. е. чтобы выполнялось равенство
.
С точки зрения геометрии задача с начальными условиями сводится к тому, чтобы из семейства интегральных кривых (4) выделить ту, которая проходит через точку 
плоскости.
Определение 8. Задача отыскания решения уравнения (2), удовлетворяющего начальным условиям
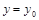при ,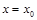
называется задачей Коши.