Вычисление площади криволинейной трапеции
Пусть на отрезке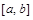 
определена непрерывная функция 
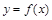и будем пока что считать, что 
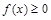для всех 
.
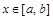Определение 1.Фигуру, ограниченную кривой 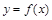, отрезком 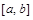оси 
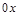, прямым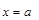и 
и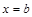 
, называют криволинейной трапецией.
В отдельных случаях может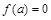 
или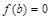 
и тогда соответствующая сторона трапеции сжимается в точку.
Для вычисления площади S этой криволинейной трапеции поделим отрезок 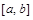произвольным образом на п частей точками
.
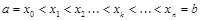Длины этих частей
.
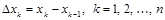Перпендикуляры к оси проведены из точек деления к кривой , разделяют всю площадь трапеции на п узких криволинейных трапеций.
 | |||
| |||
Заменим каждую из этих трапеций прямоугольником с основанием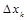 
и высотой 
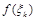, где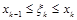 
.
Сумма площадей всех таких прямоугольников будет равняться
.
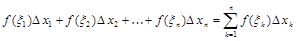Таким образом, площадь S криволинейной трапеции приближенно равняется этой сумме, т.е.
.
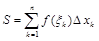Эта формула будет тем точнее, чем меньше величина .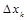
Чтобы получить точную формулу для вычисления площади S криволинейной трапеции, надо в этой формуле перейти к пределу, когда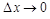 
. Тогда
.
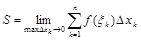Определение определенного интеграла и его содержание
Пусть функция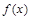 
задана на отрезке 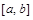. Разобьем этот отрезок на п частей точками деления
.
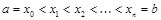В каждом промежутке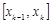 
длиной 
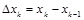выберем произвольную точку 
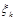и вычислим соответствующее значение функции
.
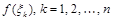Получим сумму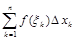 
, которую называют интегральной суммой для функции 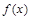на отрезке .
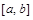Определение 2. Если существует конечный предел интегральной суммы при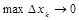 
, независимый от способа разбиения отрезка 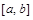на части и выбора точек 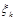, то этот предел называется определенным интегралом от функции 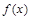на отрезке 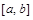и обозначается
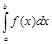. (1)
Математически это определение можно записать так:
= 
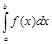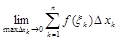(2)
Числа а и b называются нижним и верхним пределом интегрирования.
Функция 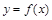называется подинтегральной функцией, а 
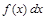– подинтегральным выражением.
Согласно этому формулу для вычисления площади S криволинейной трапеции теперь можно записать в виде
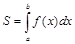. (3)
Основные свойства определенного интеграла
Из определения неопределенного интеграла и основных теорем о пределах вытекают следующие свойства
1. 
.
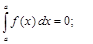
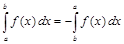2.Для любых чисел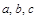 
имеет место равенство
.
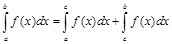3.Постоянный множитель можно выносить за знак определенного интеграла, т.е
.
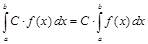4. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их определенных интегралов:
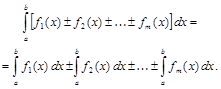
5.Если функция 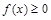всюду на отрезке 
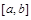, то
.
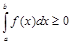6.Если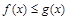 
всюду на отрезке 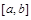, то
.
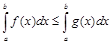7. Если функция 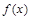интегрируема на отрезке 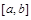, то
.
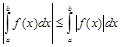8. Если М и т – соответственно, максимум и минимум функции 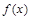на отрезке 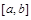, то
.
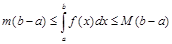