Координаты точки пересечения медиан треугольника

№	А	В	С	№	А	В	С
	1, 1	-3,-2	3,-4		3, 0	-1,-6	-3, 1
	1,-1	-3, 1	3, 3		3, 1	-1, 4	-3,-1
	1, 2	-3,-1	0,-2		3,-1	-1, 1	0,-4
	-1, 1	-3,-2	2,-2		0, 3	6,-1	-1,-3
	-1, 2	6, 0	0,-2		0,-3	4, 6	-1,-2
	-1, 0	3, 4	6,-2		-3, 0	2, 3	6,-1
	0, 1	4, 3	6,-1		3, 4	-1, 1	2,-1
	1, 0	-3,-2	3,-3		4, 3	6,-1	1, 0
	0,-1	-6, 1	-4,-5		4,-3	1, 1	7, 2
	2, 1	-3, 0	-1,-5		-3, 4	0,-2	6, 1
	2,-1	0, 6	-5, 0		1, 0	0, 2	-1, 1
	2, 3	-2, 5	-6, 0		0, 1	-2, 0	-1,-1
	-3, 2	2, 3	6, 1		2, 1	0, 3	-1, 2
	3, 2	-2, 5	-1, 5		-1, 0	2, 2	5,-2
	-3,-2	0,-5	5, 0		0,-2	5, 2	7,-4

4.Даны вершины пирамиды ABCD. Найти:

1) периметр основания АВС;

2) угол между ребрами АВ и AD;

3) площадь грани АВС;

4) уравнение плоскости АВС;

5) проекцию АВ на AD;

6) объем пирамиды ABCD;

7) длину высоты пирамиды DO;

8) канонические уравнения прямой, проходящей через точку D перпендикулярно плоскости ABC.

№	A	B	C	D
	1, 0, 0	0, 2, 1	2, 3, 4	-2, 1, 3
	2, 0, 0	1, 2, 2	-1, 1, 1	3,-1, 1
	3, 0, 0	1, 1, 1	2, 1, 0	-1, 2, 2
	-1, 0, 0	2, 1, 0	3, 2,-1	1, 1, 1
	-2, 0, 0	2, 1, 2	3,-1, 2	1, 2, 1
	-3, 0, 0	3, 1, 1	2,-1, 2	1, 2, -1
	1, 1, 0	2, 0, 1	1, 3, 0	0, 0, 4
	1, 2, 0	-2, 0, 1	0, 3, 4	3, 1, 2
	1, 3, 0	3, 1, 2	-1, 2, 1	-2, 1,-1
	1,-1, 0	2, 1, 1	-1, 2, 2	0, 0, 3
	1,-2, 0	2, 0, 0	0,-2, 1	4, 1, 2
	1,-3, 0	3, 0, 1	2, 1, 2	-1, 2, 3
	2, 1, 0	3, 2, 2	1, 0, 1	-1, 3, 3
	2, 2, 0	1, 3, 1	-1, 1, 2	3,-1, 3
	2,-2, 0	-1, 3, 4	-1, 4, 2	1,-2, 2
	-2, 1, 0	1,-1, 1	2, 2, 2	3, 0, 3
	-2,-1, 0	1, 1,-1	3, 2, 1	4, 0, 2
	2, 0, 1	3, 2, 2	-1, 1, 0	0,-1, 3
	3, 0, 1	4, 2, 2	2,-1, 1	-2, 2, 0
	1, 0, 1	2,-2, 3	0, 1, 2	3, 3, 0
	-2, 0, 1	2, 2, 2	1, 1, 3	-1, 3,-1
	-2, 0,-1	2,-1, 0	1, 1, 1	3, 4, 2
	2, 0, 2	3, 1, 1	1, 2,-1	-1, 3, 0
	3, 0, 2	2, 2, 1	4, 1, 0	-1, 4, 3
	3, 0, 4	1, 1, 3	2,-1,-1	4, 2, 1
	2, 0, 4	1, 1, 2	-1, 2, 0	0,-1, 3
	2, 0, 0	0, 0, 0	1,-1, 0	1, 1, 0
	0, 0, 1	0, 0,-2	1, 0, 0	0,-1, 1
	1, 1,-1	1, 0, 0	0, 1, 0	0, 0, 1
	0, 1,-1	1,-1, 0	2, 1,-1	3, 2, 1

5.Даны векторы в некотором базисе. Показать, что векторы образуют базис. Найти координаты вектора в этом базисе.

№
	-2, 4, 7	0, 1, 2	1, 0, 1	-1, 2, 4
	6, 2,-1	1, 3, 0	2,-1, 1	0,-1, 2
	1,-4, 4	2, 1,-1	0, 3, 2	1,-1, 1
	-9, 5, 5	4, 1, 1	2, 0,-3	-1, 2, 1
	-5,-5, 5	-2, 0, 1	1, 3,-1	0, 4, 1
	13, 2, 7	5, 1, 0	2,-1, 3	1, 0,-1
	-9, -1, 7	0, 1, 1	-2, 0, 1	3, 1, 0
	3,-3, 4	1, 0, 2	0, 1, 1	2,-1, 4
	3, 3,-1	3, 1, 0	-1, 2, 1	-1, 0, 2
	-1, 7,-4	-1, 2, 1	2, 0, 3	1, 1,-1
	6, 5,-4	1, 1, 4	0,-3, 2	2, 1,-1
	5,15, 0	1, 0, 5	-1, 3, 2	0,-1, 1
	6,-1, 7	1,-2, 0	-1, 1, 3	1, 0, 4
	2,-1,11	1, 1, 0	0, 1,-2	1, 0, 3
	11, 5,-3	1, 0, 2	-1, 0, 1	2, 5,-3
	8, 0, 5	2, 0, 1	1, 1, 0	4, 1, 2
	3, 1, 8	0, 1, 3	1, 2,-1	2, 0,-1
	8, 1,12	1, 2,-1	3, 0, 2	-1, 1, 1
	-9,-8,-3	1, 4, 1	-3, 2, 0	1,-1, 2
	-5, 9,-3	0, 1,-2	3,-1, 1	4, 1, 0
	-5, 5,6	0, 5, 1	3, 2,-1	-1, 1, 0
	8, 9, 4	1, 0, 1	0,-2, 1	1, 3, 0
	23,-4,30	2, 1, 0	1,-1, 0	-3, 2, 5
	3, 1, 3	2, 1, 0	1, 0, 1	4, 2, 1
	-1, 7, 0	0, 3, 1	1,-1, 2	2,-1, 0
	11,-1, 4	1,-1, 2	3, 2, 0	-1, 1, 1
	0,-8, 9	0,-2, 1	3, 1,-1	4, 0, 1
	-3, 2,18	1, 1, 4	-3, 0, 2	1, 2,-1
	8,-7,-13	0, 1, 5	3,-1, 2	-1, 0, 1
	2, 7, 5	1, 0, 1	1,-2, 0	0, 3, 1

6. Преобразовать уравнение кривой второго порядка к каноническому виду, построить ее и найти параметры, определяющие данную линию.

1).	2).
3).	4).
5).	6).
7).	8).
9).	10).
11).	12).
13).	14).
15).	16).
17).	18).
19).	20).
21)	22).
23).	24).
25).	26).
27).	28).
29)	30).

Глава 3 ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

Функция, предел, непрерывность функций

3.1.1 Функция, основные понятия

Пусть даны два независимых множества Х и Y.

Определение 1. Соответствие 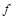, которое каждому элементу сопоставляет один и только один элемент , называется функцией и записывается , .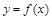

Определение 2.Множество Х называется областьюопределения функции f и обозначается . Множество всех называется множеством значенийфункции f и обозначается

Пример 1. Найти область определения функции

.

Решение.Функция у существует, если подкоренное выражение неотрицательное. Поэтому область определения находится из неравенства:

Таким образом, областью определения данной функции есть отрезок .

Четность, нечетность, периодичность функций

Пусть функция 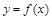задана на промежутке , который симметричен относительно начала координат.

Определение1.Функция 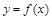, определенная на промежутке , называется четной, если для любого выполняются условия ;

График четной функции симметричен относительно оси ординат.

Определение 2. Функция 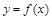, определенная на промежутке , называется нечетной, если для любого выполняются условия ;

График нечетной функции симметричен относительно начала координат.

Пример 1. Пусть , где . Согласно известному свойству данной функции,

Следовательно, 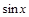является нечетной функцией.

Пример 2. Пусть , где . Известно, что

Итак, 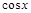является четной функцией.

Определение 3. Функция 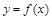, определенная на всей числовой оси, называется периодической, если существует число такое, что для всех выполняется тождество

Число Т при этом называется периодом функции .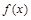

Если число Т является периодом функции 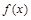, то и число –Т есть также периодом :

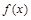Если 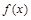— периодическая функция с периодом Т, то функция , где , есть периодической с периодом .

В частности, если рассмотреть функцию , где — постоянные, то периодом этой функции есть число .

Пример 3. Найти период функции .

Решение. Функция 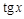имеет период , поэтому функция имеет период .