Основные элементарные функции и их графики

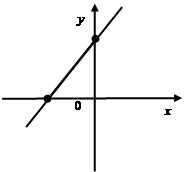Линейная функция:

.

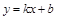График функции – прямая (для построения достаточно две точки, желательно точки пересечения с осями координат):

х2

; .

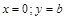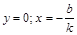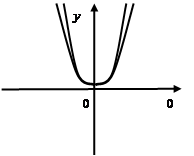Степенная функция:

х

.

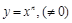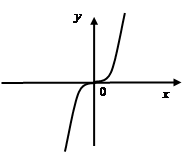Если 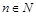, функция определена на всей числовой оси, т.е. .

х3

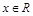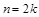Если — функция четная, то принимает значение 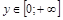. Их графиками будут параболы соответственно второго, четвертого и т.д. порядков. Если 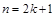— графики парабол третьего, пятого и т.д. порядков.

Показательная функция:

.

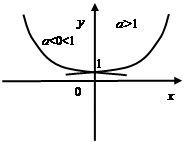
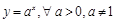Область ее определения 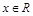, область значений 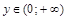. Если 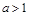, функция ­, если 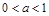, функция ¯.

Причем, для произвольного 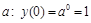, т.е. график произвольной экспоненты проходит через точку .

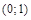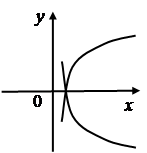
Логарифмическая функция:

а>1

.

0<a<1

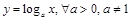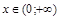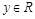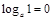Эта функция обратная к показательной, , , . Поэтому график произвольной функции проходит через точку .

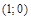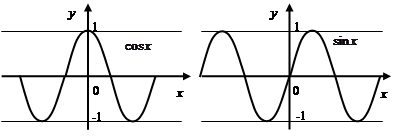
Тригонометрические функции:

.

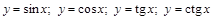Функци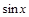и и 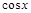определены для всех 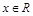и имеют множество значений .

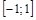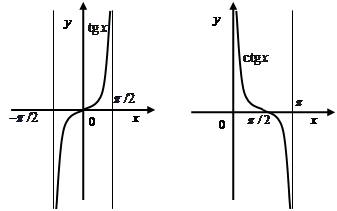
Функция 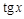определена всюду, кроме 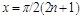, , 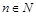и монотонно возрастает в каждом интервале области определения.

Функция 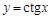всюду определена, кроме 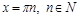, и монотонно убывает в каждом интервале области определения.

Множество значени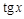й и 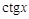— промежуток .

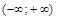Функции 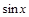, , 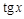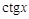— нечетные, их графики симметричны относительно начала координат, 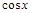— четная, ее график симметричен относительно .

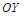Функции периодические. Наименьший период синуса и косинуса 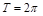, 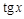и — .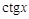

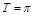Тригонометрические функции в интервале монотонности имеют обратные:

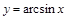— обратная к 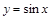на отрезке ;

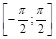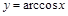— обратная к 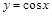на отрезке ;

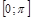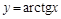— обратная к 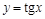на промежутке ;

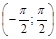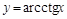— обратная к 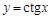на промежутке .

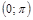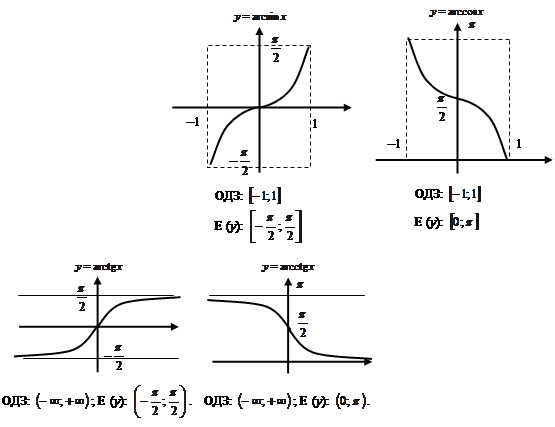
Предел функции

Пусть функция 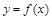определена в некоторой окрестности точки 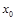, кроме, может быть, самой точки .

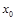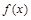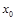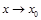Определение 1.Число А называется пределом функции в точке при , если для любого положительного 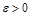найдется число 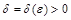такое, что при всех 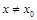, 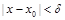выполняется неравенство 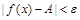. При этом пишут .

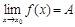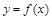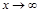Определение 2. Число А называется пределом функции при , если для произвольного 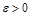существует число 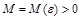такое, что при 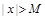выполняется неравенство 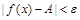. При этом пишут .

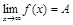Определение 3. Функция 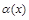называется бесконечно малой при 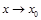, если .

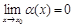Определение 4. Функция 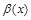называется бесконечно большой при 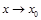, если .

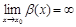Аналогично определяются бесконечно малые и бесконечно большие величины при .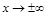

Очевидно, что всякая б.б.ф. в окрестности точки 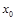является неограниченной в этой окрестности.

Однако, если 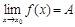, где 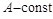, то функция 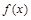ограничена в окрестности точки .

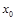Бесконечно большие величины находятся в тесной связи с бесконечно малыми: если при данном предельном переходе функция 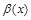есть бесконечно большой, то функция 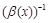при этом самом предельном переходе будет бесконечно малой и наоборот.