Классификация экономико – математических моделей и основные требования к ним

Модели, бесконечные в своем многообразии, можно классифицировать по самым различным признакам. Прежде всего, все модели можно подразделить на физические и описательные. И с теми и с другими мы постоянно имеем дело, даже не замечая этого, как не замечаем, например, того, что говорим прозой.

Описательные модели различаются по языку описания на словесно-описательные (вербальные), математические и графи­ческие. В частности, к описательным относятся модели, в кото­рых моделируемый объект описывается с помощью слов, черте­жей, математических зависимостей и т. д. К таким моделям мож­но отнести литературу, изобразительное искусство, музыку, хореографию и т. д.

К описательным моделям относятся и экономико-матема­тические модели (ЭММ), которые по общему целевому назна­чению делятся на теоретико-аналитические, используемые при изучении общих свойств и закономерностей экономических систем, и прикладные, применяемые для решения конкретных экономических задач системного анализа.

По степени агрегирования объектов моделирования модели различаются на макроэкономические, описывающие функцио­нирование всей экономической системы в целом, и микроэконо­мические, исследующие системы уровня фирмы, предприятия, отдельного подразделения фирмы и т. п.

По характеру учета фактора времени экономико-математические модели подразделяются на статические, в которых все зависимости относятся к единому моменту времени, и динами­ческие, описывающие процесс развития экономической системы во времени.

По учету фактора случайности экономико-математические модели классифицируются на детерминированные, если в них результаты на выходе однозначно определяются управляющими воздействиями, и вероятностные (стохастические), если при за­дании на входе модели определенной совокупности значений на ее выходе могут получаться различные результаты в зависимо­сти от действия случайного фактора.

По цели создания и применения выделяют балансовые модели, выражающие требования соответствия наличия факто­ров производства и их использования; оптимизационные моде­ли, предназначенные для выбора оптимального, т. е. наилучше­го по конкретному критерию, решения; и, наконец, алгоритми­ческие модели, предназначенные для использования в режиме машинной имитации исследуемых экономических систем.

Экономико-математические модели могут быть классифи­цированы также по типу математического аппарата, использу­емого для их решения: линейные, нелинейные, модели теории массового обслуживания, модели теории игр и т. д.

Переходя к рассмотрению основных требований к постро­ению ЭММ, необходимо прежде всего отметить, что при ее формализации необходимо четко установить следующее.

1. Цели функционирования объекта, т. е. те конечные резуль­таты, которые необходимо получить путем выбора тех или иных воздействий на моделируемый объект. Математически они фор­мализуются в виде так называемых целевых функций модели.

2. Условия функционирования объекта, т. е. ограничиваю­щие обстоятельства при достижении поставленных целей, фор­мально записываемые в виде системы ограничений. Ограниче­ния модели в известной степени дополняют цели, взаимодействуя, таким образом, с ними.

Важнейшим требованием к любой экономико-математи­ческой модели является адекватность модели, т. е. соответствие модели исследуемой системе (объекту, процессу). При этом необходимо отдавать себе отчет в том, что никакая модель не может быть полным (точным) отображением исследуемого объек­та во всей его сложности: модель по ее определению требует некоторого упрощенного представления моделируемой системы. Модель всегда абстрактна, и все дело заключается, очевидно, в том, от каких реальных свойств конкретного объекта следует абстрагироваться, чтобы «с водой не выплеснуть ребенка».

Абстрактный характер экономико-математических моделей побуждает людей несведущих расценивать эти модели как нечто непрактическое и нереалистичное. В действитель­ности экономико-математические модели эффективны и практич­ны именно потому, что они представляют собой абстракции. Мир реальности слишком сложен и запутан, чтобы его можно было представить строго упорядоченным. Экономико-математи­ческие модели позволяют нам лучше понимать действительность именно потому, что они игнорируют сбивающие с толку детали действительности.

Более того, известно, что познавательная ценность различ­ных теорий и концепций во многом определяется как раз таким критерием, как их пригодность для абстрактного моделирования социально-экономических процессов, что и обеспечивает необхо­димую глубину понимания изучаемых процессов и явлений.

Применение моделей именно потому и целесообразно, что они позволяют отвлечься от несущественных с точки зрения целей их использования деталей.

Экономико-математические модели эффективны лишь тог­да, когда они отражают важнейшие черты изучаемого процесса, отвлекаясь от тех или иных сторон реального явления, имеющих второстепенное значение для решения данной конкретной зада­чи. Разумная абстракция, допустимая идеализация модели не­обходимы для выявления основных закономерностей процесса и для обеспечения возможностей практического использования мо­делей.

Таким образом, при построении любой экономико-матема­тической модели ее разработчику необходимо стремиться к тому, чтобы выделить и воспроизвести (формализовать) только те свойства и характеристики реальных объектов, которые необхо­димы и достаточны для решения поставленной задачи. При разработке модели необходимо учитывать в ней только наибо­лее существенные (эффективные) факторы и условия.

Очевидно при этом, что существенность условий функцио­нирования объекта должна оцениваться, прежде всего, с точки зрения критерия цели. Например, если речь идет о модели чело­века для детских игр, то эта модель (игрушка) должна быть в определенной степени похожа на человека. А если моделируется (испытывается) новая парашютная система, то в качестве модели человека достаточно взять мешок с песком определенного веса.

Таким образом, при формализации любой ЭММ необходи­мо соответствие между целевой установкой и мерой абстракции, которая должна быть необходимой и достаточной для реализа­ции именно этой, а не какой-либо другой цели. Сформулирован­ное положение может быть названо принципом информационно-целевой адекватности.

Из данного принципа со всей очевидностью следует, что конкретную экономико-математическую модель необходимо использовать, имея в виду строго определенную область ее при­менения. При оценке же экономико-математической модели важ­но понимать, что она не может быть одинаково эффективной абсолютно для всех исследуемых объектов — это такой же нонсенс, как, скажем, универсальное транспортное средство. Ведь никто же не критикует автомобиль за то, что он не летает. К сожалению, аналогичная ситуация в области экономико-матема­тического моделирования не является редкостью.

Важным практическим требованием, предъявляемым к экономико-математическим моделям, является требование их эффективной реализуемости. Необходимость соблюдения данного требования заставляет при построении конкретной экономико-математической модели стремиться к тому, чтобы получить модель, принадлежащую к хорошо изученному классу матема­тических структур, желательно линейных, для которых суще­ствует достаточно универсальный и эффективный метод их решения — так называемый симплексный метод, основная идея которого рассматривается нами в приложении.

Иногда это удается сделать путем некоторого упрощения исходных предпосылок модели, не искажающего существенных черт моделируемого объекта. Чаще же всего экономисты ис­пользуют линейные структуры не потому, что они убеждены в простоте анализируемых фактов, а из-за математических труд­ностей, связанных с нелинейной оптимизацией. В этих достаточ­но сложных условиях (сложных потому, что линейных задач практически не существует) чрезвычайно важным становится умение математика строить линейные модели, более или менее адекватно описывающие нелинейные условия функционирова­ния того или иного объекта.

Естественно поэтому говорить об искусстве экономико-ма­тематического моделирования в сочетании с научными принци­пами построения моделей.

Рассмотрим конкретный простейший пример, иллюстриру­ющий данное утверждение.

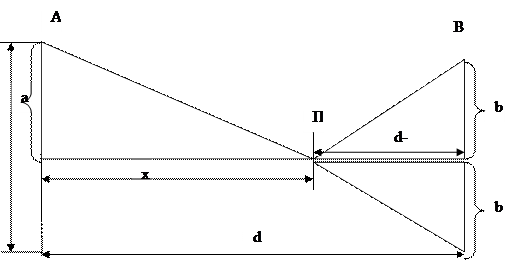
Два населенных пункта А к В расположены по одну сторону от прямолинейного участка железной дороги на расстоянии соответственно а и b Определить, где должна быть размещена одна платформа П, чтобы соединяющие ее с населенными пунктами прямолинейные участки шоссейной дороги имели наименьшую суммарную длину (при прочих равных условиях)?

Графическая иллюстрация постановки задачи приводится на рис.3.

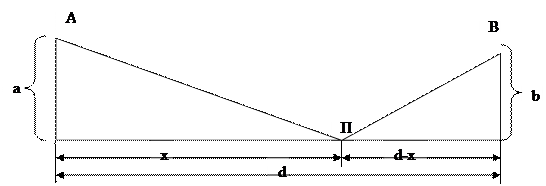Рисунок 1.3 Графическая модель «нетворческого» решения задачи

Математическая, кстати, нелинейная модель, соответствующая рис.3, имеет следующий вид:

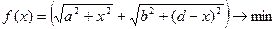
Осуществим ее решение.

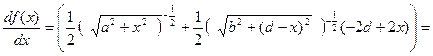
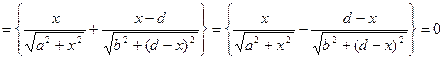
Отсюда

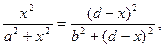
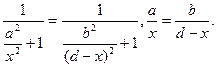
В результате получим:

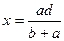
Если же к построению математической модели данной за­дачи подойти творчески, то ее соответствующая графическая интерпретация может иметь вид, представленный на рис. 1.4.

Рисунок 1.4 Графическая иллюстрация искусства моделирования

Соответствующая рис. 1.4 линейная модель, не требу­ющая никакой оптимизации, будет следующей:

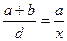
Откуда

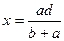
Очевидно, естественно, что при решении конкретных прак­тических задач могут иметь место ситуации, когда формализа­ция экономической проблемы, несмотря на все искусство ма­тематика, приводит к очень сложной или даже неизвестной ранее математической структуре. Тогда для решения такой модели может потребоваться разработка специального алгоритма или даже оригинального математического аппарата.

Таким образом, разрабатывая экономико-математическую модель, исследователь системы должен всегда иметь в виду, как получить ее решение, ибо от успешной реализации этого этапа моделирования зависит успех всего исследования.

Особое место в системе требований, предъявляемых к экономико-математическим моделям, занимает необходимость их реализации в диалоговом режиме.

Выше уже отмечалось, что экономико-математичес­кая модель не может отразить все многообразие факторов, дей­ствующих в сколько-нибудь сложных экономических системах. В этих условиях обязательным требованием к моделям стано­вится их реализация в так называемом режиме диалога со спе­циалистом (менеджером), хорошо знающим моделируемый объект. Реализация экономико-математической модели в таком режиме предполагает поступление промежуточной информации от модели к специалисту, который на основе ее анализа выра­батывает конкретные управленческие решения, используемые (учитываемые) в процессе последующих реализаций модели на вычислительной технике. Такой подход значительно ускоряет процесс как разработки самой модели, поскольку наиболее трудноформализуемую часть проблемы лицо, принимающее решение (ЛПР), берет на себя, так и ее реализации на вычис­лительной технике (за счет упрощения экономико-математичес­кой модели).

Кроме того, в таком режиме обеспечивается активное уча­стие аппарата управления в процессе поиска оптимальных тра­екторий развития исследуемой экономической системы. Это обстоятельство является весьма существенным достоинством моделей, реализуемых в режиме диалога, ибо одна из распро­страненных ошибок использования экономико-математических моделей, к счастью, в настоящее время преодолеваемая, состоит в абсолютизации моделей и представлении, что они позволяют получать готовые (да еще и оптимальные) управленческие ре­шения. Необходимо совершенно отчетливо понимать, что ника­кие экономико-математические модели не могут предопределять решений: они должны лишь служить решающим звеном в их обосновании.

Необходимо исходить из того, что оптимальный план не тот, который получается в результате точного решения оптими­зационной модели, а тот, который наилучшим образом учитыва­ет знание, опыт и интуицию практических работников, интересы исполнителей плана, а также другие трудноформализуемые фак­торы. Правда, такой план точнее будет назвать рациональным.

В процессе диалога при поиске сложного решения происхо­дит естественное распределение обязанностей между лицом, при­нимающим решение, и ЭВМ: машина производит рутинную об­работку информации и оптимизирует частные решения, а ЛПР управляет расчетной процедурой, помогая машине преодолеть формально неопределенные этапы вычислений. Творческие воз­можности ЛПР дополняются в этом случае вычислительной мощью ЭВМ, реализующих на базе современных математических методов соответствующие экономико-математические модели.

Диалог пользователя с экономико-математической моделью при поиске рациональных решений осуществляется в так называемых точках диалога. Приведем для иллюстрации полное множество таких точек (*) для оптимизационной модели линейного программирования:

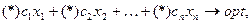
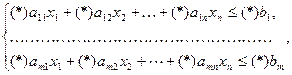
где

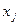- переменные модели ( );

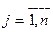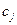- «цены» целевой функции ( );

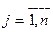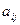- коэффициенты затрат ресурса 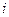-го вида на единицу продукции 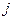-тонаименования ( , );

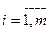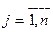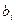- располагаемый объем ресурса 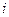-говида ( ).

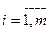Технически такой диалог с моделью может быть проведен с помощью коэффициентов {р}, {z} и {k}, вводимых ЛПР перед очередной реализацией модели в ее формализованное представление в памяти ЭВМ.

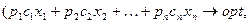
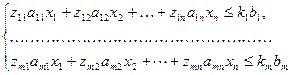
Изменение значений этих коэффициентов, соответствующее конкретным экономическим организационным мероприятиям (увеличению имеющихся объемов ресурсов, ужесточению норма­тивов затрат ресурсов, увеличению цен на изготавливаемую продукцию и др.), позволит найти рациональное решение по­ставленной проблемы. Диалог с этой моделью предполагает прежде всего анализ ресурсной обеспеченности того или иного плана, поскольку ресурсы являются как бы фильтром, сквозь который приходится пропускать принимаемое решение. Если анализ показывает, что потребность в ресурсах в результате увеличения их объемов или ужесточения нормативов удовлетво­рить невозможно, то приходится пересматривать цели и стра­тегии до тех пор, пока не будет достигнута их обеспеченность ресурсами.

Таким образом, диалоговый процесс планирования можно рассматривать как новую технологию планирования.