Моделирование случайных сигналов

К сожалению, анализ системы далеко не всегда можно выполнить теоретически. Это особенно актуально для нелинейных систем. В этом случае единственным методом остается имитационное моделирование. Поэтому важно уметь моделировать случайные процессы, действующие на систему: возмущения (например, влияние ветра и волн на судно) и помехи измерения (погрешности измерительной системы).

Обычно задана спектральная плотность 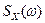и требуется получить процесс, имеющий такую спектральную плотность.

Вспомним, что спектральная плотность неотрицательна для любой частоты. Тогда функция , полученная при подстановке в 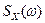, неотрицательна на мнимой оси, то есть при для всех 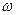. Можно доказать, что в этом случае ее можно представить в виде произведения , то есть в форме (6). При этом всегда можно выбрать передаточную функцию так, чтобы она была устойчивой (не имела полюсов в правой полуплоскости) и минимально-фазовой (не имела нулей в правой полуплоскости). Такой переход от к называется факторизацией (англ. разложение на множители).

Как следует из (6), если на вход звена с передаточной функцией подать единичный белый шум, процесс на выходе будет иметь заданную спектральную плотность 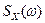. Функция называется передаточной функцией формирующего фильтра.

Проще всего моделировать процессы с рациональной спектральной плотностью. Например, одна из моделей морского волнения описывается спектром

,

где – дисперсия волновой ординаты, – коэффициент затухания и – частота максимума спектра. Заменяя на , получаем

.

Очевидно, что формирующий фильтр будет иметь передаточную функцию вида

,

так что

.

Приравнивая коэффициенты числителя и знаменателя и , сразу находим:

, , .

В более сложных случаях факторизация выполняется с помощью численных методов. Нужно разложить на простейшие сомножители числитель и знаменатель и включить в только те множители, корни которых находятся в левой полуплоскости.

Итак, формирующий фильтр мы построили. Теперь остается один очень практический вопрос: как получить белый шум, который, как известно, является сигналом с бесконечной энергией? Вспомним, что белый шум – это только вспомогательный сигнал, который, проходя через систему с передаточной функцией , генерирует сигнал с заданной спектральной плотностью. Оказывается, можно заменить его на другой сигнал (который просто получить на компьютере), и при этом спектральная плотность выхода оказывается достаточно близка к заданной.

Известно, что на компьютере легко получить случайную последовательность чисел с равномерным или нормальным распределением. По этим числам можно построить ступенчатый сигнал, фиксируя каждое значение в течение некоторого времени :

Теоретически эти числа некоррелированы; при этом можно показать, что корреляционная функция 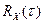ступенчатого сигнала – треугольная (см. рисунок справа). При она равна дисперсии последовательности случайных чисел, а при обращается в нуль (потому что моменты времен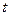и и 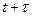находятся на разных интервалах и, следовательно, соответствующие значения некоррелированы). Число называют интервалом корреляции – так называется интервал, после которого можно считать корреляционную функцию (примерно) равной нулю.

Взяв преобразование Фурье от корреляционной функции

получаем спектральную плотность

.

Вычисляя предел этой функции при , находим , так что при выборе это значение равно 1 (как у белого шума). Заметим, что , когда , то есть при любом целом . Форма спектральной плотности показана на рисунке ниже (здесь и далее принимается ):

Конечно, это далеко не белый шум, у которого спектральная плотность должна быть постоянной на всех частотах. Тем не менее, при уменьшении интервала корреляции «колокол» расширяется, и для низких частот можно считать, что . В пределе при спектр стремится к равномерному спектру единичного белого шума. Далее будет показано, что при грамотном выборе такой сигнал можно использовать в качестве источника вместо белого шума.

Для примера предположим, что нужно получить сигнал со спектральной плотностью , то есть формирующий фильтр имеет передаточную функцию . В качестве входного сигнала для этого звена будем использовать описанный выше ступенчатый сигнал при с. На рисунке приведены графики спектральной плотности ступенчатого сигнала (синяя линия), желаемой спектральной плотности (сплошная зеленая линия) и фактической спектральной плотности выхода (штриховая линия).

По графику видно, что в существенной полосе частот (где частотная характеристика звена ненулевая) спектр входного сигнала существенно неравномерный, поэтому желаемый и фактический спектры на выходе системы немного различаются в области высоких частот. Приняв , имеем совершенно другую картину:

Спектр входного сигнала в интересующей нас области практически равномерный, в спектр реального выхода практически точно совпадает с заданным.

Очевидно, что при выборе нужно учитывать частотные свойства формирующего фильтра, точнее, полосу частот, где его частотная характеристика достаточно отличается от нуля. Для этого используют понятие полосы пропускания системы – так называется частота, для которой амплитудная частотная характеристика уменьшается на 3 дБ (децибела) в сравнении с максимальным значением (составляет примерно 0,708 от максимума). Разработчики Matlab рекомендуют при моделировании использовать значение

.

В нашем случае амплитудно-частотная характеристика (апериодического звена) имеет вид , ее максимум равен 1 (при ), поэтому полоса пропускания определяется равенством . Отсюда следует , так что .