Закон Ома в операторной форме
Рассмотрим цепь r,L,C (рис. 14-1), которая была подключена к источнику e1(t) и в момент t=0 переключается к источнику e(t)
Закон Ома для мгновенных значений после переключения запишется так:
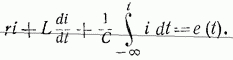
Нижний предел интеграла, равный –(бесконечность) берется в том случае, к моменту переключения рубильника t=0 режим в цепи установился, т. е. к источнику э. д. с. e1(t) цепь была включена в момент времени t=–(бесконечность) (только при этих условиях режим к моменту переключения рубильника теоретически мог установиться).
Если к моменту переключения режим не установился, то в качестве нижнего предела нужно брать —t1, где t1 — время, прошедшее с момента включения источника e1(t) до момента t=0
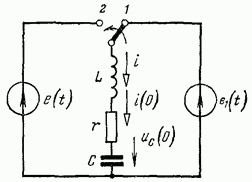
Рис. 14-1.
Постановка у интеграла нижнего предела, равного –(бесконечность) или –t1 имеет целью подчеркнуть, что в момент коммутации конденсатор уже был заряжен, т. е.
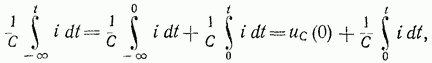 (14-16)
(14-16)
где Uc(0) — напряжение на емкости в момент переключения, т. е. при t=0
Чтобы перейти от закона Ома, записанного для мгновенных значений (оригиналов), к его выражению в операторной форме, нужно в соответствии с формулой (14-1) поступить так: умножить обе части равенства (14-15) на e^(-pt)*dt и проинтегрировать от нуля до (бесконечность). Тогда получим:
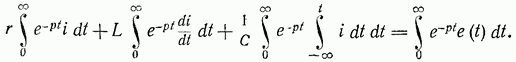
Полагая, что
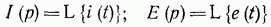
и учитывая формулы (14-4), (14-7) и (14-16), получаем следующее алгебраическое уравнение:
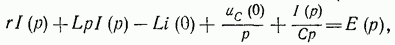
откуда получается закон Ома в операторной форме для цепи r,L,C.
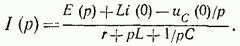
Последнее равенство справедливо и в том случае, когда процесс переключения рубильника еще не был установившимся. В обоих случаях под i(0) и Uc(0) надо понимать ток в индуктивности и напряжение на емкости в момент переключения рубильника. Заметим,
что в соответствии со сказанным выше нужно было бы писать i(0+) и Uc(0+). Но так как ток в индуктивности и напряжение на емкости не изменяются скачком при t=0 будем писать короче: i(0) иUc(0).
Выражение, стоящее в знаменателе, назовем полным сопротивлением цепи r,L,C в операторной форме или операторным сопротивлением
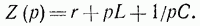 (14-18)
(14-18)
Сопротивление в операторной форме уже встречалось в § 13-14 и теперь получено вполне строго. Напомним, что сопротивление цепи r,L,C в операторной форме построено так же, как ее комплексное сопротивление, если в последнем заменить j*(омега, как w) через p. Величина, обратная операторному сопротивлению, называется операторной проводимостью:
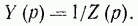
Операторная э. д. с. цепи, стоящая в числителе (14-17), состоит не только из операторного выражения внешней э.д.с., т.е. E(p), но и еще из двух слагаемых, которые определяются начальными условиями, т. е. током в индуктивности i(0)=iL(0) и напряжением на емкости Uc(0). Иными словами, наличие двух дополнительных ЭДС Li(0) и –Uc(0)/p которые можно назвать внутренними или расчетными э. д. с., указывает на то, что в магнитом поле катушки и вэлектрическом поле конденсатора в момент коммутации была запасена энергия. Положительные направления этих э. д. с. выбраны совпадающими с положительным направлением тока ветви.
Заметим, что, как и ранее, положительные направления тока и напряжения на конденсаторе считаются совпадающими. Если же до коммутации конденсатор был заряжен и, стало быть, положительное направление напряжения на нем до коммутации Uc- было задано, а положительное направление тока через конденсатор выбрано противоположным положительному направлению Uc- внутренняя или расчетная э. д. с., обусловленная емкостью, должна быть взята с обратным знаком, т. е. +Uc(0)/p.
Особенно просто выглядит выражение (14-17) при нулевых начальных условиях, т. е. при iL(0)=0 и Uc(0)=0:
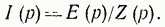 (14-19)
(14-19)
Тогда оно полностью аналогично закону Ома в комплексной форме.
Вопрос16
