II. Работа по теме урока. 1. Тренировочные упражнения: № 376 (д, е); 377 (г); 378 (г), 380, 379 (д)

1. Тренировочные упражнения: № 376 (д, е); 377 (г); 378 (г), 380, 379 (д).

2. Самостоятельная работа (ДМ, В – 2, 3, № 77–80).

Вариант I

1. Решите с помощью уравнения задачу: «Петя задумал число. Если вычесть его из числа 333, то получится 195. Какое число задумал Петя?».

2. Решите уравнения:

а) 965 + n = 1505; б) 802 – х = 416.

3. Решите уравнение: 44 + (а – 85) = 105.

4. Угадайте корень уравнения и выполните проверку:

8 – у = у + 2.

Вариант II

1. Решите с помощью уравнения задачу: «Если из задуманного числа вычесть 242, то получится 120. Каково задуманное число?».

2. Решите уравнения:

а) х + 223 = 1308; б) с – 127 = 353.

3. Решите уравнение: 69 + (87 – n) = 103.

4. Угадайте корень уравнения х + 7 = 11 – х и сделайте проверку.

III. Домашнее задание:п. 8–10; № 399, 397 (в); 401; 403 (б). Подготовиться к контрольной работе.

Урок № 37

Контрольная работа № 3 (п. 8–10)

Вариант I

1. Найдите значение выражения (m – 148) – (97 +n), если

m = 318, n = 45.

2. Решите уравнения:

а) у – 27 = 45 б) 37 + х = 64; в) 63 – (25 +z) = 26.

3. На отрезке АВ отмечены точки С и D так, что точка D лежит между точками С и В. Найдите длину отрезка DB, если АВ = 56 см, АС = 16 см и CD = n см. Упростите получившееся выражение и найдите его значение при n = 18 и при n = 29.

4. Упростите выражения:

а) m + 527 + 293; б) 456 – (146 + m).

5. На отрезке АМ = 22 см отметили точку К, такую, что АК = 16 см, и точку Р, такую, что РМ = 17 см. Найдите длину отрезка КР.

Вариант II

1. Найдите значение выражения (m + 124) – (356 – n), если m = 186,
n = 287.

2. Решите уравнения:

а) 67 – z = 28; б) у + 56 = 83; в) (х +26) – 29 = 19.

3. На отрезке CD отмечена точка N. Найдите длину отрезка CD, если отрезок CN равен 45 см, а отрезок ND короче отрезка CN на n см. Упростите получившееся выражение и найдите его значение при n = 54 и при n = 36.

4. Упростите выражения:

а) 638 + n + 272; б) 623 – (m + 343).

5. На отрезке АВ = 16 см отметили точку М, такую, что АМ = 14 см, и точку N, такую, что BN = 12 см. Найдите длину отрезка MN.

III. Домашнее задание:решить другой вариант.

Урок № 38

Умножение натуральных чисел (п. 11)

Цели:сформировать понятие умножения как сложения одинаковых слагаемых, повторить названия чисел при умножении.

Оборудование: плакат или пленка к кодоскопу с устными упражнениями.

Ход урока

I. Устные упражнения.

1. 436 (а, б).

2. Угадайте корень уравнения: (плакат)

а) х + х = 64; б) 58 + у + у + у = 58; в) а + 2 = а – 1.

3. Придумайте задачу, которая решалась бы с помощью уравнения:
х + 15 = 45.

II. Изучение нового материала.

1. Изложение материала можно проводить в соответствии с учебником, привлекая учащихся к работе с ним.

На доске и в тетрадях учащихся можно сделать записи:

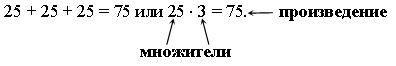
2. Что значит число m умножить на натуральное число n?

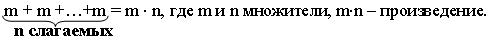
3. Как правильно читать выражения вида: 175 × 60? (Ответ учащиеся найдут в рубрике Г).

III. Закрепление.

1. № 404, 405 (а, б, в); 412 (а, в, д, ж), 413 (а), 406.

Устно: № 433, 431 (а, в).

2. На повторение: устно № 446 (а, в).

IV. Итог урока.

1. Ответить на вопросы (1–5) после п. 11.

2. Закончить фразу.

а) сумму одинаковых слагаемых можно заменить…

б) выражение m × n называется…

в) числа в выражении m × n называются…

г) если один из множителей увеличить в 1000 раз, а другой множитель оставить без изменения, то произведение…

V. Домашнее задание:п. 11 (до свойств); № 450 (а), 451 (а, б); 455 (а, в), 462 (а), 458 (а).

В математический словарь: множимое, множитель, сомножители, произведение.

Урок № 39

Умножение натуральных чисел

И его свойства (п. 11)

Цели:повторить свойства умножения, научить представлять число в виде произведения, вырабатывать навык использования свойств умножения при вычислениях.

Оборудование: набор карточек с числами.

Ход урока

I. Устные упражнения.

1. При умножении каких двух чисел получится 30 (45, 100)? (Учитель показывает карточку с числом.)

2. Какую цифру надо приписать справа к цифре 3, чтобы получилось двузначное число, которое делится на 7 (на 6, на 4)?

3. Вычислить устно:

8000 × 8 280 : 40

60 × 900 1000 : 50

800 × 20 70 × 30

900 × 300 200 × 400.

4) Решите числовой кроссворд (начертить заранее на доске).

А			Б	В
		Г
	Д		Е
Ж			З

По горизонтали:

А. 7 × 7 = … Б. 8 × 3 = …

Ж. 4 × 9 = … З. 6 × 7 = …

По вертикали:

А. 6 × 8 = … В. 9 × 5 = …

Г. 7 × 9 = … Д. 8 × 7 =…

Е. 9 × 6 =…

II. Изучение нового материала.

1. Излагается в соответствии с учебным материалом п. 11.

2. Обратить внимание на буквенную запись свойств умножения и их формулировку. (Можно составить опорный конспект.)

III. Закрепление.

1. 416 (а, б, г); 431 (б, г); 407, 411, 423, 424 (а, в, д), 412 (з, к).

(Подчеркнутые номера можно решить самостоятельно).

2. На повторение: устно № 446 (а, в).

IV. Итог урока.

1. Ответить на вопросы к п. 11.

2. Тест.

1) Равенство m × (n × k) = (m × n)×k является:

а) переместительным свойством умножения;

б) сочетательным свойством умножения;

в) другим каким-то свойством умножения.

2) Равенство 49 × 0 = 0 при помощи букв записывается:

а) b × 0 = 0; б) 0 × b = b; в) b × 49 = 49.

3) Произведение чисел 4 × 222 × 5 равно:

а) 8885; б) 4445; в) 4440.

4) Сколько существует способов разложения числа 20 на два множителя:

а) 3 способа; б) 2 способа; в) 4 способа.

V. Домашнее задание:п. 11 (до свойств); № 449 (б), 450 (в, г), 453, 455 (б, г, д), 462 (а), 458 (б).

Урок № 40
Умножение натуральных чисел

И его свойства (п. 11)

Цели:закрепить навык умножения натуральных чисел «в столбик» и умение применять действия умножения при решении задач.

Оборудование: кодоскоп, пленки, плакаты для устных упражнений и опорный конспект; каждому ученику текст заданий № 434.

Ход урока

I. Устные упражнения.

1. Вычислите применяя свойства умножения (кодоскоп):

а) 4 × 33 × 25; б) 12 × 75; в) 48 × 12.

2. Как изменится произведение, если один из множителей увеличить в 3 раза, другой в 2 раза?

3. В каких случаях произведение двух чисел равно одному из них?

4. Восстановите цепочку вычислений (вывешивается плакат):

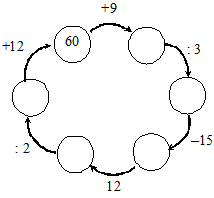
5. Какое число пропущено?

6. Среди чисел 1, 0, 5, 11, 9 найдите корни уравнений:

а) х + 19 =30; в) 30 + х = 32 – х;

б) 27 – х = 27 + х; г) 10 + х + 2 = 15 + х – 3.

7. № 446 (е, ж, з).

8. Повторение теоретического материала.

Вывешивается плакат:

1) а × b = b × a a × 0 = 0

2) (a × b) × c = a × (b + c) a × 1 = a

3) a(b + c) – ab + ac

Учитель показывает равенство, ученик называет, что оно обозначает, и формулирует.