Интегралы от выпуклых функций
При решении многих задач целесообразно применять следующий подход.
Разделим отрезок [a,b], на котором задана непрерывная функция f. на n частей точками 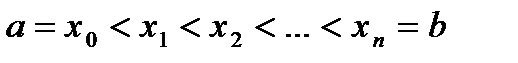 . Построим прямоугольные трапеции, основаниями которых являются отрезки xkyk, xk+1yk+1, а высотами – xkxk+1, k=0,1,…,n-1. Сумма площадей этих трапеций при достаточно большом n близка к площади криволинейной трапеции. Чтобы этот факт можно было применить к доказательству неравенств функция f должна удовлетворять некоторым дополнительным требованиям.
. Построим прямоугольные трапеции, основаниями которых являются отрезки xkyk, xk+1yk+1, а высотами – xkxk+1, k=0,1,…,n-1. Сумма площадей этих трапеций при достаточно большом n близка к площади криволинейной трапеции. Чтобы этот факт можно было применить к доказательству неравенств функция f должна удовлетворять некоторым дополнительным требованиям.
Пусть функция f дважды дифференцируема на некотором промежутке и в каждой точке этого промежутка f//(x)>0. Это означает, что функция f/ возрастает, т.е. при движении вдоль кривой слева направо угол наклона касательной к графику возрастает. Иными словами, касательная поворачивается в направлении, обратном направлению вращения часовой стрелки. График при этом «изгибается вверх», «выпячиваясь вниз». Такая функция называется выпуклой. График выпуклой функции расположен «ниже» своих хорд и «выше» своих касательных. Аналогично, если f//(x)<0, то f/ убывает, касательная вращается по часовой стрелке и график лежит «выше» своих хорд, но «ниже» своих касательных. Такая функция называется вогнутой.
Функция 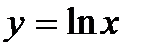 вогнута в области своего определения, так как
вогнута в области своего определения, так как 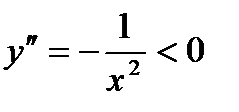 . Вторая производная функции
. Вторая производная функции 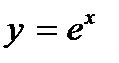 положительна на всей числовой прямой. Поэтому
положительна на всей числовой прямой. Поэтому 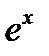 – выпуклая функция. Для функции
– выпуклая функция. Для функции 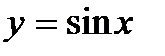 вторая производная
вторая производная 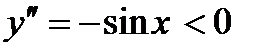 при
при 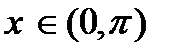 ,
, 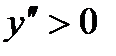 при
при 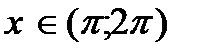 , т.е. функция
, т.е. функция 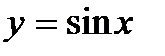 на интервале
на интервале
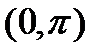 вогнута, а на
вогнута, а на 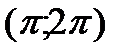 выпукла.
выпукла.
Задача 2.7. Доказать, что 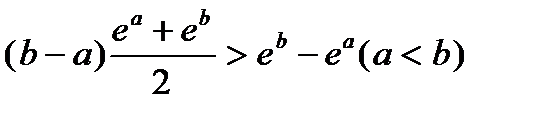
Решение.
Левая часть этого неравенства равна площади прямоугольной трапеции, основания которой равны значениям функции 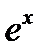 в точках
в точках 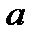 и
и 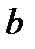 , т.е.
, т.е. 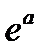 и
и 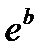 , а высота –
, а высота – 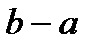 . Функция
. Функция 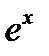 выпуклая. Поэтому площадь криволинейной трапеции, ограниченной ее графиком, прямыми
выпуклая. Поэтому площадь криволинейной трапеции, ограниченной ее графиком, прямыми 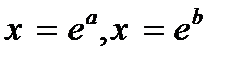 и отрезком [a,b] оси x, меньше площади прямоугольной трапеции. Итак,
и отрезком [a,b] оси x, меньше площади прямоугольной трапеции. Итак,
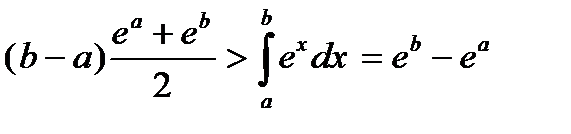 .
.
Подобный результат имеет место и в общем случае. Пусть функция f на отрезке [a.b] непрерывна, положительна и выпукла. Тогда
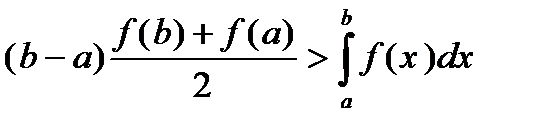 (2.9)
(2.9)
Если же непрерывная, положительная функция f вогнута, то
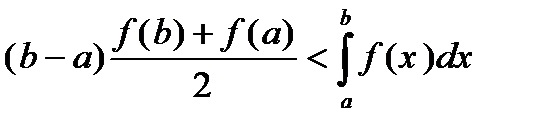 (2.10)
(2.10)
2.4. Некоторые классические неравенства и их применение
Приведем вывод некоторых замечательных неравенств с помощью интегрального исчисления. Эти неравенства широко используются в математике, в том числе и при решении элементарных задач.
Пусть y=f(x) – непрерывная возрастающая при x>0 функция. Кроме того, f(0)=0, f(a)=b, где a, b некоторые положительные действительные числа. Из школьного курса математики известно, что если функция f возрастает и непрерывна на некотором промежутке, то существует функция f-1, обратная функции f. Ее область определения совпадает с множеством значений f. функция f-1 непрерывна и возрастает в области своего определения.
Отсюда следует, что для данной функции f существует непрерывная возрастающая обратная функция f-1 такая, что f-1(0)=0, f-1(b)=a. Графики зависимостей y=f(x) и x=f-1(y) совпадают.
Площадь S1 криволинейной трапеции, ограниченной линиями y=f(x), y=0, x=0, x=a, равна 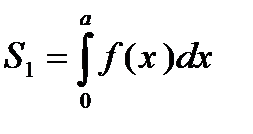 .
.
Площадь S2 криволинейной трапеции, ограниченной линиями x=f-1(y), x=0, y=0, y=b, равна 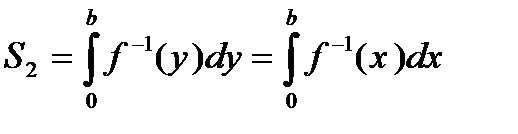
В последнем равенстве мы пере обозначили переменную интегрирования, что, конечно, несущественно при вычислении интеграла. Поскольку площадь прямоугольника равна сумме площадей S1 и S2, то
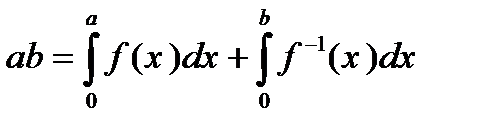
Может оказаться, что f(a) не равно заданному числу b, т.е. f(a)>b или f(a)<b.
В каждом из этих случаев площадь прямоугольника меньше суммы площадей криволинейных трапеций, равной S1+S2.
Объединяя эти три случая, получаем следующий результат.
Пусть f и f-1 – две непрерывные возрастающие взаимно обратные функции, обращающиеся в нуль в начале координат. Тогда для a>0, b>0 имеет место неравенство
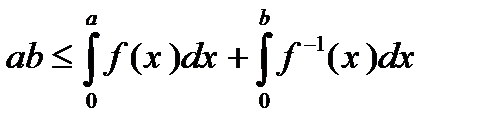 (2.13)
(2.13)
Равенство имеет место тогда и только тогда, когда b=f(a). Это неравенство называют неравенством Юнга. Оно является источником получения других важных неравенств.
Пример 2.10. Функция f, где f(x)=x, удовлетворяет условиям, при которых справедливо соотношение (1). Далее.,f-1(x)=x. Поэтому
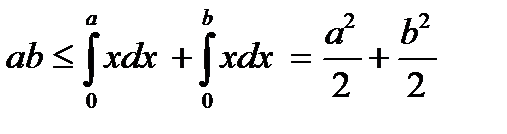 (2.14)
(2.14)
