Получение уравнений движения

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ

«Московский энергетический институт»

Кафедра «Мехатроники и теоретической механики»

ОТЧЕТ

о научно-исследовательской работе

Студент аспирантуры 1 курса	Е.А. Антонов
( Семестр: 1 )
по направлению	01.06.01 «Математика и механика»
по специальности	Теоретическая механика
Научный руководитель:	В.В. Подалков
Должность, степень, звание	проф., доктор тех. наук.

г. Москва 2016 г.

РЕФЕРАТ

Влияние малых нелинейных и нестационарных возмущений на динамику микромеханического гироскопа

Перечень ключевых слов: микромеханический гироскоп, нелинейные деформации, вынужденные колебания.

Объектами исследования и разработки в данной работе являются микромеханические устройства, в частности, гироскопы.

Целью данной работы является рассмотрение, математическое описание и анализ поведения микромеханического гироскопа в режиме вынужденных колебаний при наличии в системе нелинейных деформаций и их влияние на динамику резонатора.

Методы исследования в первую очередь определялись специфическими особенностями рассматриваемого гироскопа и его математической модели. В ходе исследования были использованы основы теоретической механики, метод малого параметра и осреднения, теория дифференциальных уравнений, системы и методы аналитического и матмоделирования. Были использованы системы символьных вычислений Maple и Mathematica.

Результаты работы:

В ходе работы был рассмотрен микромеханический гироскоп L-L типа, для которого была составлена математическая модель. В рамках принятой математической модели было проанализировано влияние медленно меняющихся параметров, в частности, частоты внешней силы и рассмотрено влияние нелинейности.

Содержание

Введение 5

Основная часть проведенной работы 7

Постановка задачи 7

Получение уравнений движения 7

Анализ динамики резонатора 8

Числовой пример 9

Заключение11

Список литературы12

Введение

Последние десятилетия проходят под знаком интенсивного развития микросистемной техники. Такая техника, в свою очередь, требует высокоточных и миниатюрных датчиков, качественных и эффективных микродвигателей, качественных преобразователей и т.д. В данной отрасли широкое применение находят микромеханические гироскопы. Их развитие, а именно нахождение новых технологических схем и решений, получение высокой точности при малых размерах и массы – довольно сложная и актуальная проблема на сегодняшний день [7, 12, 17, 19, 21, 23].

Микромеханические гироскопы (ММГ) имеют огромный потенциал, что позволяет им господствовать на рынке из-за своих малых размеров и малого энергопотребления. Это один из наиболее быстро растущих сегментов современного рынка. Область применения микромеханических гироскопов интенсивно расширяется. Сейчас эти устройства можно найти во многих приборах современного мира: от бытовой техники и игровых устройств до аэрокосмической промышленности [14 - 16, 20, 22].

На сегодняшний день актуальна задача проектирования и создания новейших систем навигации [3, 4] и систем управления на основе довольно интересного класса инерциальных датчиков – микромеханических гироскопов L-L типа.

В работе [13] С.П. Тимошенковым и его соавторами был рассмотрен ММГ L-L типа. Представлен совершенно уникальный вариант геометрии, позволяющий использовать его в системах, управляющих высокоскоростными вращающимися объектами. Полученные в работе математические модели делают возможным анализ динамики чувствительного элемента.

Влияние нелинейных динамических эффектов на поведение микромеханического гироскопа L-L типа описано в статье А.М. Лестева и А.В. Ефимовской [9]. Сделаны выводы по части устойчивости инерциальной массы, а конструкция с двумя инерциальными массами имеет самую высокую степень стабильности технических характеристик.

Также влияние нелинейных эффектов на динамику гироскопов подробно разобраны в работах [8, 10, 11, 18].

Данная работа продолжает изложенные в статье [1] исследования динамики ММГ с чувствительным элементом в виде массы, закрепленной на упругом подвесе.

Основная часть проведенной работы

Постановка задачи

Конструкция рассматриваемого микромеханического гироскопа представлена на рисунке 1:

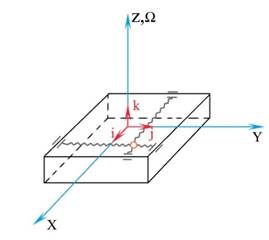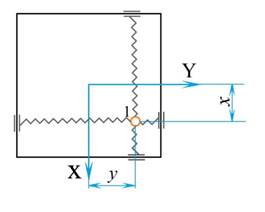Рисунок 1 – Модель ММГ

Она представляет собой точечную массу 1 (резонатор), закрепленную в рамке с помощью упругих торсионов, моделируемых пружинами жесткости c. Торсионы, в свою очередь, обеспечивают резонатору одну степень свободы вдоль оси Y и одну степень свободы вдоль оси X (рис. 1).

Целью данной работы является изучения влияние нелинейных деформаций на динамику микромеханического гироскопа в режиме вынужденных колебаний на подвижном основании.

Получение уравнений движения

Кинетическая энергия системы имеет следующий вид:

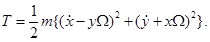
где: x, y – координаты точечной массы в системе координат, связанной с рамкой; m - масса системы; Ω - угловая скорость основания, на которое помещен гироскоп.

Удельная потенциальная энергия деформации системы записывается следующим образом:

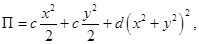
где c – жесткость торсионов; d – параметр, характеризующий нелинейные упругие свойства резонатора.

В таком случае лагранжиан системы равен:

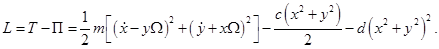(1)

Используя формализм Лагранжа и учитывая, что на систему действует внешняя вынуждающая сила, моделируемая гармоникой fcosψ, получим дифференциальные уравнения движения чувствительного элемента микромеханического гироскопа:

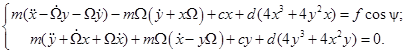(2)