Проверка правильности умозаключений

Правильность умозаключения можно проверить двумя способами.

Во-первых, мы можем построить таблицу истинности и показать, что всякий раз, когда гипотезы истинны, истинно и заключение. Во-вторых, мы можем использовать таблицы истинности для обоснования правил вывода, а затем использовать правила вывода для доказательства справедливости заключения. Длинные умозаключения, как правило, проще обосновывать при помощи правил вывода (см. п. 1.5).

Рассмотрим метод проверки правильности умозаключений, альтернативный методу таблиц истинности. Пока предлагается принять метод на веру, вернувшись к его обоснованию несколько позже. Это непрямой метод, поскольку он направлен на доказательство неправильности умозаключения. В случае успеха такого доказательства это будет свидетельством неправильности умозаключения. Если, предполагая неправильность умозаключения, мы приходим к противоречию, то умозаключение является правильным. Например, рассмотрим умозаключение

A 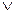B

A C

B C

------------

C

Если умозаключение неправильное, существуют истинностные значения A, B и C,

для которых посылки истинны, а заключение ложно. Если заключение ложно, то C ложно. Если B C истинно , а C ложно, то B должно быть ложно. Аналогично, если A C истинно, а C ложно тогда A должно быть ложно. Но тогда A 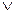B ложно, что приводит к противоречию с утверждением, что заключение ложно, а посылки истинны. На основании этого делаем вывод, что умозаключение правильно.

Правила вывода

Перечислим некоторые правила вывода, на которые мы будем ссылаться в

дальнейшем:

а) Правило отделения (Modus Ponens)

A B

A

________

B

б)Силлогизм

A B

B C

_________

A C

в) Modus Tollens

A B

˥B

__________

˥A

г) Расширение

A

________

A˅B

д) Специализация

A ˄ B

___________

A

е) Конъюнкция

A

B

_________

A ˄ B

ж) Выбор

A

A (B˅C)

B D

C D

__________

D

з)Исключающий выбор

A (B ˄ ˥B)

A˅ C

__________

C

и) Сведение к абсурду

˥A (B ˄ ˥B)

____________

A

В большинстве аксиоматических систем теоремы и аксиомы могут быть весьма сложными, а их переплетение с правилами вывода — весьма запутанным. Сейчас мы попытаемся объяснить, что происходит в процессе доказательства и как доказательства конструируются. Сложные доказательства обычно представляют собой длинную цепочку правильных умозаключений вышеуказанных типов. Поэтому доказательство можно определить как последовательность утверждений, каждое из которых истинно в силу одной из следующих причин:

а) по предположению;

б) по аксиоме или определению;

в) по ранее доказанной теореме или лемме;

г) выведено из предыдущих утверждений;

д) логически эквивалентно предыдущему утверждению.