Аксиоматические системы
Это должен быть набор аксиом (постулатов), принимаемых нами без доказательств, удовлетворяющих следующим трем условиям:
1) Независимость (любую из принятых аксиом нельзя вывести из остальных, так, что выведенная из других аксиома является не аксиомой, а теоремой)
2) Непротиворечивость (система аксиом не порождает противоречащих друг другу утверждений, то есть, ни из какой аксиомы не следует утверждение и его отрицание)
3) Полнота (систему нельзя дополнить независимым от уже принятых аксиом утверждением, то есть никакая дополнительная аксиома не может быть выведена из уже имеющихся)
Замечание 1.6.
Исходные понятия математической теории не определяются. Ведь всякое определение содержит другие понятия, логически предшествующие определяемому; поэтому по крайней мере первое определение теории обязательно содержит неопределяемые понятия, которые и принимаются за исходные. В качестве исходных обычно выбираются понятия, в понимании которых не возникает существенных разногласий; более точно: различия в понимании которых не нарушают правильности ни одного положения теории.
Парадоксы
Определение 1.7.
Парадоксом называется умозаключение, все посылки которого логически корректны, истинны, а заключение при этом абсурдно.
В более широком смысле к парадоксам относят:
1) утверждения, которые кажутся ложными, но в действительности истинны;
2) утверждения, которые кажутся истинными, но в действительности ложны;
3) рассуждения, которые кажутся безупречными, но приводят к логическому противоречию (парадоксы этого типа обычно принято называть логическими ошибками);
4) утверждения, истинность или ложность которых недоказуемы.
К известным историческим парадоксам, сильнее всего повлиявшими на развитие математики, можно отнести, среди прочих, парадоксы Зенона и Галилея. Сформулируем их:
Парадоксы Зенона ( современным языком; показывают, что движение, образец «видимого» изменения, логически невозможно.)
- Дихотомия: Чтобы пересечь комнату, сначала нужно преодолеть половину пути. Но затем нужно преодолеть половину того, что осталось, затем половину того, что осталось после этого, и так далее. Это деление пополам будет продолжаться до бесконечности, из чего делается вывод, что вам никогда не удастся пересечь комнату.
-Ахилл и черепаха: Древнегреческий герой Ахилл собирается состязаться в беге с черепахой. Если черепаха стартует немного раньше Ахилла, то ему, чтобы ее догнать, сначала нужно добежать до места ее старта. Но к тому моменту, как он туда доберется, черепаха проползет некоторое расстояние, которое нужно будет преодолеть Ахиллу, прежде чем догнать черепаху. Но за это время черепаха уползет вперед еще на некоторое расстояние. А поскольку число таких отрезков бесконечно, быстроногий Ахилл никогда не догонит черепаху.
- Стрела : в каждый момент времени летящая стрела занимает место, равное ей по протяженности, следовательно она не движется.
- Стадион : две равные по длине колонны людей, движутся параллельно с равной скоростью в противоположных направлениях. Время, за которое колонны пройдут друг мимо друга, составляет половину времени, нужного одному человеку, чтобы пройти мимо всей колонны.
Парадокс Галилея.
P1 Если X является (точным) подмножеством множества Y , то число элементов множества Х не совпадает с числом элементов множества Y
P2 Если существует взаимно-однозначное соответствие между элементами множеств X и Y, то у этих множеств одинаковое число элементов
P3 Множество четных натуральных чисел – точное подмножество множества натуральных чисел
P4 Существует взаимнооднозначное соответствие между элементами множества четных натуральных и (всех) натуральных чисел
_________
Тогда (Заключение) : Число элементов множества четных чисел не совпадает с числом элементов множества натуральных чисел и
Число элементов множества четных чисел совпадает с числом
элементов множества натуральных чисел, что является противоречием.
(Более подробно о множествах см Лекцию 2, о взаимнооднозначном соответствии Лекцию 9)
Высказывания, зависящие от параметра. Кванторы
Определение 1.8. (1)
Вместо слов "существует", "найдется", "имеется" в логических формулах употребляется символ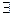 
(перевернутая первая буква английского слова exist — существовать), называемый символом (квантором) существования, а вместо слов "любой", "каждый", "произвольный", "какой бы ни" — символ 
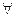(перевернутая первая буква английского слова all — "все"), называемый символом (квантором) всеобщности.
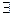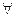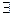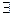Так, запись х читается "существует x", а запись x — "любое x" или "для любого x" или "для всех x". Соответственно запись x, у, или, короче, 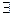х,у означает "существуют x и y", а запись 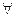x, 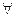y, или, короче, 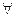x,y — "любые x и у" или "для любых х и у".
Определение 1.8.(2)
Пусть A(x) – высказывание, причем при разных значениях x оно может иметь разную истинность. x носит название параметра, а A(x) – высказывания, зависящего от параметра.
Например, A = {x2 > 5} для x=1 A(1) ложно, а для x = 11 A(11) – истинно.
Пример 1.8.
Если A(х) — утверждение "х — студент", а утверждение B(x) — "x учится
усердно", то утверждение 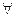x (A(x) 
B(x)) может быть интерпретировано как
"Все студенты учатся усердно". Точно так же, если A(х) — утверждение "х — кот", a B(x) — утверждение "х любит читать", то выражение 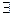x (A (x)˄ B(x)) может быть сформулировано как "Некоторые коты любят читать". Утверждение "Все люди смертны" логически может быть выражено как 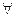x (A(x) B(x)), где A(х) — утверждение "х — человек", a B(x) — утверждение "х смертен". Аналогично, утверждение "Некоторые целые числа делятся на 5" может быть записано 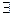x (A (x)˄ B(x)), где A(х) — утверждение "х
— целое число", a B(x) — утверждение "х делится на 5". Обычно логические выражения, содержащие 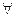x, можно превратить в утверждения, содержащие "для всех", а логические выражения, содержащие 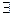x, можно обратить в утверждения, содержащие "для некоторого".
В силу такого характера перевода с языка логики на естественные языки и обратно, отрицание утверждения типа "для всех" есть утверждение типа "для некоторого", а отрицание утверждения типа "для некоторого" есть утверждение типа "для всех". Например, отрицание утверждения «Все целые числа являются простыми» есть утверждение Некоторые целые числа не являются простыми, а отрицание утверждения «Некоторые студенты любят ходить на вечеринки» есть утверждение «Все студенты не любят ходить на вечеринки».
Иначе говоря:
Пусть Â = A(x), истинное для всех x, не зависит от параметра
Ă = A(x), истинное хотя бы для одного значения параметра x
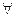 = ( x : A(x) истинно)
Ă = ( 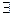x : A(x) истинно)
Построим теперь для них отрицания.
˥ Â = (A ложно хотя бы для одного значения x)
Т.е. ( 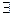x : A(x) ложно) = ( 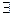x : ˥A(x) истинно)
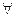˥( x : A(x) истинно) = ( 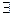x : ˥A(x) истинно)
˥ Ă = (A ложно для всех значений x)= ( 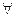x : A(x) истинно)
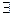˥( x : A(x) истинно) = ( 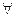x : ˥A(x) истинно)
Замечание 1.8.
Обратите внимание, что при отрицании A(x) меняется на ˥A(x) , квантор 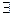на 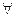и наоборот, квантор 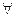на 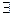.