Законы эквивалентности
Модуль 1.
Лекция 1. Элементы логики
1.1.Высказывания и утверждения. Операции над высказываниями.
1.2. Законы эквивалентности
1.3. Понятие умозаключения. Правильные умозаключения
1.4. Проверка правильности умозаключений
1.5. Правила вывода
1.6. Аксиоматические системы
1.7. Парадоксы
1.8. Высказывания, зависящие от параметра. Кванторы
Программные положения
В лекции 1 «Элементы логики» рассматриваются понятия утверждения, логической операции, умозаключения, принципы, лежащие в основе математических доказательств.
Методические рекомендации к изучению лекции
Внимательно прочитайте текст лекции и посмотрите видео-фрагмент. Выполните практические задания, придумайте собственные примеры. Некоторую проблему представляют два момента: 1) непривычные обозначения, а также которые придется запомнить и 2) различие понятия истинности в логике и «обычной жизни». Обратите внимание на понятие аксиомы, аксиоматической системы
Литература
Я.Стюарт «Концепции современной математики» Глава 1 «Математика в целом» (стр.9-18) глава 20 «Основания математики» (стр.351-368)
Дополнительно
М.Гарднер «А ну-ка, догадайся»
И.Лакатос «Доказательства и опровержения»
Р.Линдон «Заметки по логике»
Контрольные вопросы
1. Что такое высказывание? Приведите свои примеры. Приведите примеры предложений, не являющихся высказываниями
2. Какие операции можно проводить над высказываниями? Приведите свои примеры
3. Что такое умозаключение? Как можно проверить его правильность?
4. С помощью логических таблиц проверьте утверждение замечания 1.1.
5. С помощью логических таблиц и альтернативным способом проверьте правильность умозаключения:
˥( A ˄ B)
˥C  B
B
______
A  C
C
6. Что называется парадоксом?
7. Какое высказывание называется зависящим от параметра? Приведите свои примеры
8. Запишите с помощью кванторов высказывания
- на каждой улице будет праздник
- некоторые студенты прогуливают лекции
- каждый психоаналитик знаком с трудами З.Фрейда
Высказывания и утверждения. Операции над высказываниями
Определение 1.1.
Высказывание — это утверждение или повествовательное предложение, о котором можно сказать, что оно истинно или ложно, но не то и другое одновременно. Истинность и ложность высказывания относятся к данному моменту времени, например, «сегодня пятница» истинно в пятницу и ложно в другие дни недели. Иными словами, утверждение об истинности или ложности высказывания должно иметь смысл. Истинность или ложность, приписываемые некоторому утверждению, называются его значением истинности, или истинностным значением.
Обозначения
Высказывания обозначают заглавными латинскими буквами (реже – строчными латинскими). Их выбирают либо из начала латинского алфавита, либо начиная с буквы P ( от “Proposition” – высказывание). Само высказывание помещается в фигурные скобки. P = {И.В.Иванов является студентом ВЕИП}. Математические утверждения, в том числе и записанные в символьной форме также, очевидно, являются высказываниями. Иногда для упрощения, когда контекст позволяет, высказывания пишутся просто в кавычках.
Примеры 1.1 (1)
1)Примеры высказываний:
A = {Данная лекция относится к курсу «Высшая математика»}
B = {Сейчас осень}
C = {На дворе стоит лето1546 от Рождества Христова}
D = {В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы}
E = { sin π/6 = 1/2}
2) Примеры предложений, не являющихся высказываниями:
Кто вы? (вопрос),
Обязательно прочтите текст лекций по курсу высшей математики (приказ или восклицание),
Это утверждение ложно (внутренне противоречивое утверждение).
В обыденной речи для образования сложного предложения из простых используются связки — особые части речи, соединяющие отдельные предложения. Наиболее часто употребляются связки и, или, нет, если ... то, только если, и тогда и только тогда. В отличие от обыденной речи, в логике смысл таких связок должен быть определен однозначно. Истинность сложного высказывания однозначно определяется истинностью или ложностью составляющих его частей. Высказывание, не содержащее связок, называется простым. Высказывание, содержащее связки, называется сложным.
Истинность и ложность принято обозначать буквами И и Л (T от truth – правд, истина и F от false – неправда, ложь) или 1 и 0.
Для определения истинности или ложности высказывания составляют таблицу истинности. Таблица истинности перечисляет все возможные комбинации истинности и ложности сложных высказываний.
Между высказываниями можно поставить знак равенства, если их таблицы истинности совпадают.
Действия над высказываниями:
1) Логическая сумма (дизъюнкция), в обыденной речи ей соответствует союз «или»
A ˅ B – новое высказывание, истинное тогда, когда истинно хотя бы одно из высказываний A или B.
| A | B | A ˅ B |
| И | И | И |
| И | Л | И |
| Л | И | И |
| Л | Л | Л |
A={все зебры полосатые}
B={все крокодилы клетчатые}
A ˅ B ={все зебры полосатые или все крокодилы клетчатые} – новое высказывание, оно истинно, поскольку истинно высказывание A.
2) Логическое произведение (конъюнкция), в обыденной речи ей соответствует союз «и»
A ˄ B – новое высказывание, истинное тогда, когда истинны оба высказывания A и B.
| A | B | A ˄ B |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | Л |
A={все зебры полосатые}
B={все крокодилы клетчатые}
A ˄ B ={все зебры полосатые и все крокодилы клетчатые} – новое высказывание, оно ложно, поскольку истинно только высказывание A, но не B
3) Импликация (следование), соответствует обороту «если A, то B» «из A следует B», «для того, чтобы B необходимо, чтобы A».
A  B – новое высказывание, истинное всегда, кроме случая, когда A истинно, а B ложно
B – новое высказывание, истинное всегда, кроме случая, когда A истинно, а B ложно
| A | B | A  B B |
| И | И | И |
| И | Л | Л |
| Л | И | И |
| Л | Л | И |
A={все зебры полосатые}
B={все крокодилы клетчатые}
С={у тигров нет хвостов}
A  B = { если все зебры полосатые, то все крокодилы клетчатые} новое ложное высказывание
B = { если все зебры полосатые, то все крокодилы клетчатые} новое ложное высказывание
B  C = {если все крокодилы клетчатые, то у тигров нет хвостов} – новое высказывание, являющееся истинным, хотя это несколько расходится со здравым смыслом
C = {если все крокодилы клетчатые, то у тигров нет хвостов} – новое высказывание, являющееся истинным, хотя это несколько расходится со здравым смыслом
4) Логическая эквивалентность (равнозначность) , соответствует оборотам «A равнозначно B», «A тогда и только тогда, когдаB» «для того, чтобы A необходимо и достаточно, чтобы B»
A 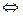 B – новое высказывание, истинное тогда, когда A и B имеют одинаковую истинность.
B – новое высказывание, истинное тогда, когда A и B имеют одинаковую истинность.
| A | B | A 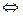 B B |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | И |
A={все зебры полосатые}
B={все крокодилы клетчатые}
С={у тигров нет хвостов}
A 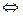 B = {Все зебры полосатые тогда и только тогда , когда все крокодилы клетчатые} – ложное высказывание
B = {Все зебры полосатые тогда и только тогда , когда все крокодилы клетчатые} – ложное высказывание
B 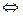 C = {Для того, чтобы все крокодилы (были) клетчатыми необходимо и достаточно, чтобы у тигров не было хвостов}. С истинностью этого высказывания легче примириться, если вспомнить, что B и C равнозначны, что вполне может относиться и к чепухе.
C = {Для того, чтобы все крокодилы (были) клетчатыми необходимо и достаточно, чтобы у тигров не было хвостов}. С истинностью этого высказывания легче примириться, если вспомнить, что B и C равнозначны, что вполне может относиться и к чепухе.
5) Отрицание (опровержение) , соответствует частице «не» и обороту «неверно, что A}
˥A (также используются обозначения Ā, ~A) – новое высказывание, истинное тогда, когда А ложно
| A | ˥A |
| И | Л |
| Л | И |
A={Вася изучает психологию}
˥A = {Вася не изучает психологию}-истинно, если Вася психологию не изучает (А ложно)
Замечание 1.1.
С импликацией A  B (п.4)) связаны высказывания
B (п.4)) связаны высказывания
Конверсия: B  A
A
Контрапозиция: ˥B  ˥A
˥A
Инверсия: ˥A  ˥B
˥B
Используя таблицы истинности можно показать, что логически эквивалентными являются импликация и контрапозиция, конверсия и инверсия. Импликация же и инверсия таковыми не являются.
Как было сказано выше, с помощью логических связок можно образовывать новые (сложные) высказывания, истинность которых можно определить опять же с помощью логических таблиц
Рассмотрим высказывание
«Вася выплатит кредит на покупку машины или Вася утратит свою
машину и будет ходить на работу пешком.
Пусть A обозначает высказывание «Вася выплатит кредит за машину, B — высказывание
«Вася останется при своей машине», а C — высказывание «Вася будет ходить
на работу пешком. Тогда наше сложное высказывание можно представить в виде
A˅((˥B)˄C)
где скобки использованы, чтобы показать, какие именно высказывания являются
компонентами каждой связки.
Таблица истинности дает возможность однозначно указать те ситуации, когда высказывание A˅((˥B)˄C) является истинным.
Поскольку исходных высказываний 3 – A, B и C, каждое из них может быть истинным или ложным, всего возможно 23 комбинаций истинности-ложности, то есть в нашей таблице истинности будет 8 строк
| A | B | C | ˥B | (˥B)˄C | A˅((˥B)˄C) |
| И | И | И | Л | Л | И |
| Л | И | И | Л | Л | Л |
| И | Л | И | И | И | И |
| И | И | Л | Л | Л | И |
| Л | Л | И | И | И | И |
| Л | И | Л | Л | Л | Л |
| И | Л | Л | И | Л | И |
| Л | Л | Л | И | Л | Л |
Законы эквивалентности
Законы эквивалентности позволяют заменить в высказывании любую его компоненту на логически эквивалентное ей высказывание. Полученное в результате такой замены высказывание будет логически эквивалентно исходному, поскольку истинностное значение высказывания зависит исключительно от истинностных значений составляющих его компонент (но не от их формы или сложности).
Теорема 1.1. Некоторые законы логической эквивалентности
а) Законы идемпотентности
A˄A = A,
A˅A = A
б) Закон двойного отрицания
˥(˥A) = A
в) Законы де Моргана
˥ (A˅B) = ˥ A ˄ ˥B;
˥(A˄B) = ˥A ˅ ˥B
г) Свойства коммутативности
A ˅ B = B ˅ A
A ˄ B = B ˄ A
д) Свойства ассоциативности
A ˅ (B ˅C) = (A ˅B)˅ C;
A ˄ (B ˄ C) = (A ˄ B) ˄ C.
е) Свойства дистрибутивности
A ˄(B ˅C) = (A ˄B) ˅(A ˄C)
A ˅(B˄ C) = (A ˅B) ˄(A ˅C)
ж) Закон контрапозиции
A  B = ˥B
B = ˥B  ˥A
˥A 
з)
A  B = ˥A ˅ B
B = ˥A ˅ B
и)
A 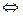 B = (A
B = (A  B) ˅ (B
B) ˅ (B  A)
A)
Докажем правомерность знака равенства между правыми и левыми частями с помощью таблиц истинности. Рассмотрим первый из законов де Моргана, остальные останутся в качестве упражнений
˥ (A˅B) = ˥ A ˄ ˥B;
| A | B | A˅B | ˥ (A˅B) | ˥ A | ˥B | ˥ A ˄ ˥B |
| И | И | И | Л | Л | Л | Л |
| И | Л | И | Л | Л | И | Л |
| Л | И | И | Л | И | Л | Л |
| Л | Л | Л | И | И | И | И |
Как мы видим, правая и левая части утверждения ложны и истинны одновременно, стало быть, утверждение о равенстве верно.
Определения 1.2.
Высказывание, истинное во всех случаях, называется логически истинным, или тавтологией. Теоремы в математике являются примерами тавтологий.
Высказывание «Вася сдаст экзамен по математике или Вася не сдаст экзамен по математике» является примером тавтологии, хотя и не очень информативным
Высказывание, построенное так, что оно ложно в каждом случае, называется логически ложным, или противоречием. «Вася сдаст экзамен по математике и Вася не сдаст экзамен по математике» является примером такого утверждения.
Покажите с помощью логических таблиц, что высказывание (A˄(A  B))
B))  B является тавтологией, а высказывание ˥((A˄(A
B является тавтологией, а высказывание ˥((A˄(A  B))
B))  B), соответственно, противоречием.
B), соответственно, противоречием.
