Импликация и эквивалентность двух предикатов

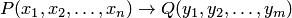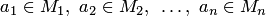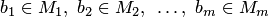Импликация определяется как такой предикат, что для любых предметов и высказывание 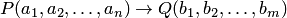является импликацией высказывани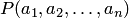й и 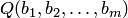. Аналогично определяется эквивалентность двух предикатов. Нетрудно проверить, что импликация двух предикатов, зависящих от одних и тех же переменных, есть тождественно истинный предикат тогда и только тогда, когда ее заключение является следствием посылки, а эквивалентность тождественно истинна, если и только если исходные предикаты равносильны. Свойства этих операций над предикатами, подобно свойствам операций отрицания, конъюнкции и дизъюнкции над предикатами (см. теорему 19.12), получаются из соответствующих тавтологий теоремы 3.3. Так, если 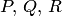— предикаты, то, например,

а) ;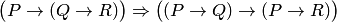
б) ;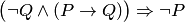
в)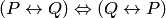

Задание для практической работы:

Найти формулы ПНФ и ССФ, выполнить унификацию

Вариант	Формула
	"x(A(x)®ù B(y))®$y(B(y)®ù A(x))
	"x(ù A(x)®$x(ù C(x)))®"x((C(x)®A(x))
	"x(A(x)®$x(B(x)))®$y(ù A(x)Úù C(y)ÚC(y)&B(x))
	"x(A(x)®$x(B(y)))®$x(ù A(x)®ù B(y))
	"x(A(x)®B(y))&"y(A(x)®(B(y)®C(z))®$z(A(x)®C(z))
	"x(A(x)®$y(B(y)®C(z)))®"z(A(x)&B(y)®C(z))
	"x(A(x)®B(z))&"y(C(y)®A(x))®$z(C(y)®B(z))
	"x(A(x)®B(y))®"y((C(y)ÚA(x))®(C(y)Ú$y(B(y)))
	"x(A(x)®B(y))&"y(A(x)®(B(y)®C(z)))®(A(x)®$z(C(z)))
	"x(A(x)®B(y)&A(x)®"y(B(y)®C(z)))®(A(x)®$z(C(z)))
	"x(A(x)®$z(B(y)®C(z)))®"y(B(y)®(A(x)®C(z)))
	("x(A(x))®$x(B(x)))®"z((B(x)®C(z))®(A(x)®C(z)))
	($x(ù A(x))®"x(ù B(x)))®(ù B(x)ÚA(x))
	("x(A(x)))®("x(B(x)))®$y(C(y)&A(x)®C(y)&B(x))
	"x(ù A(x)®$y(B(y)))®(ù B(y)®A(x))

Практическая работа № 8 « «Разбиение множества на классы»

Основные понятия и определения.

В математике бинарным отношением между любыми двумя множествам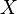и и 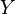(или просто на 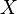, если 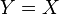) называется всякое подмножество 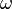декартова произведения этих множеств: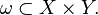

Бинарные отношения могут обладать различными свойствами, такими как

- Рефлексивность: .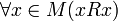

- Антирефлексивность (иррефлексивность): .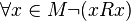

- Симметричность: .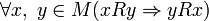

- Антисимметричность: .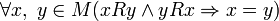

- Транзитивность: .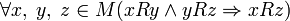

- Асимметричность: 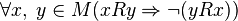. Асимметричность эквивалентна одновременной антирефлексивности и антисимметричности отношения.

Виды отношений

- Рефлексивное транзитивное отношение называется отношением квазипорядка.

- Рефлексивное симметричное транзитивное отношение называется отношением эквивалентности.

- Рефлексивное антисимметричное транзитивное отношение называется отношением (частичного) порядка.

- Антирефлексивное антисимметричное транзитивное отношение называется отношением строгого порядка.

- Полное антисимметричное (для любых x, y выполняется xRy или yRx) транзитивное отношение называетсяотношением линейного порядка.

- Антирефлексивное антисимметричное отношение называется отношением доминирования.