Обработка результатов измерений. Обработку результатов измерений можно произвести двумя способами

Обработку результатов измерений можно произвести двумя способами.

1. Графическая обработка результатов измерений. На миллиметровой бумаге построить графики зависимости периода колебаний от положения груза на стержне маятника. По оси абсцисс отложить деления шкалы, указывающие положения груза, а по оси ординат – величины периодов колебаний. Кривые Т₁(х) и Т₂(х) пересекаются. Это означает, что периоды колебаний относительно осей В₁ и В₂ совпадают, то есть опорные призмы физического маятника взаимно обратимы. Точка пересечения определяет значение периода колебаний физического маятника, приведенная длина которого равна расстоянию между опорными призмами, (l_П = 0,730 м).

По данному значению l_П и периоду колебаний, полученному из графика по точке пересечения кривых, рассчитать ускорение свободного падения, пользуясь формулой (6).

2. Обработка результатов измерений с помощью копьютера. Зависимость периода колебаний от положения груза можно аппроксимировать многочленами вида

y = a₁ + a₂x +a₃x²,

y = b₁ + b₂x +b₃x²

(для 1 и 2-й призм соответственно).

Коэффициенты a и b находят методом наименьших квадратов. Расчет этих коэффициентов, вычисление ускорения свободного падения и расчет погрешности можно произвести с помощью компьютера по специально созданной программе.

3. Расчет погрешности (для случая графической обработки результатов измерений). Найти систематическую и случайную ошибки измерения t. Для расчета случайной ошибки по методу Стьюдента использовать данные одной из таблиц (например, таблица 1), которые соответствуют значению периода, наиболее близкому к точке пересечения графиков. Рассчитать полную ошибку определения времени десяти колебаний:

Dt = ,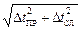

где Δt_ПР – приборная ошибка секундомера.

Принять Δt_СИСТ = 0,1 с (в нашем случае систематическая ошибка определяется конечной скоростью реакции человека). Убедиться в том, что относительная ошибка, с которой задана l_П, много меньше ошибки в определении t = t_СЛ + t_СИСТ.

Поскольку период колебаний найден на графике по точке пересечения двух кривых, то для нахождения относительной ошибки в определении периода, предполагая, что мы не допустили ошибки в определении числа колебаний, получим

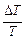= 2 .

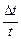В соответствии с правилами расчета ошибок косвенных измерений [4] рассчитать относительную ошибку, считая 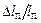= 0):

dg = = .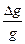

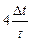Примечание

Так как значение p известно с большей точностью, то ошибка, вносимая округлением этого числа, может быть сделана заведомо меньше, чем ошибка измерений остальных величин. При вычислениях значение p достаточно принять равным 3,14.

По найденной ошибке dg найти абсолютную ошибку Δg. Результаты измерений g представить в виде g ± Δg.

Сравнить Δg с отклонением полученного значения g от значения ускорения свободного падения для Москвы, полученного более точными методами и равного 9,81 м/с².

Результат следует считать удовлетворительным, если

g – Δg ≤ 9,81 м/с² ≤ g + Δg.

Контрольные вопросы

1. От каких величин зависит период колебаний физического маятника?

2. Что называется приведенной длиной физического маятника?

3. Какая точка называется центром качания? Покажите, что центр качания и точка подвеса взаимно обратимы.

4. Как используется это свойство для определения ускорения свободного падения?

Список литературы

5. Детлаф А.А., Яворский Б.М. Курс физики. –М.: Высш. шк. – 2000.

6. Савельев И.В. Курс физики. – Т. 2. – М.: Наука – 1998 и далее.

7. Трофимова Т.И. Курс физики. – М., 2000 и далее.

8. Селезнёв В.А., Тимофеев Ю. П. Вводное занятие в лабораториях кафедры физики. – М.: МИИТ. – 2011. – 38 с.

Работа 105

ИЗУЧЕНИЕ СВОБОДНЫХ КОЛЕБАНИЙ

ФИЗИЧЕСКОГО МАЯТНИКА

Цель работы.Определение момента инерции физического маятника двумя методами, измеряя: 1) период его малых колебаний; 2) его приведённую длину.

Введение

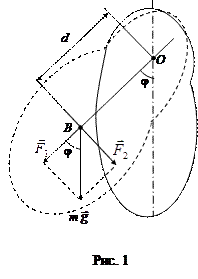Физическим маятником называется любое твердое тело, совершающее колебания под действием силы тяжести вокруг горизонтальной оси, не проходящей через центр инерции тела. Всегда можно подобрать математический маятник, синхронный данному физическому, т.е. такой математический маятник, период колебания которого равен периоду колебаний физического маятника. Длина такого математического маятника называется приведённой длиной физического маятника.

Следует отметить, что в однородном поле сил тяжести центр инерции и центр тяжести совпадают.

Тело совершает колебания под действием вращающего момента 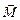, значение модуля которого:

M = F₂d, (1)

где d – кратчайшее расстояние от оси вращения до центра тяжести тела, то есть по длине равное OB, F₂ – проекция силы тяжести на перпендикулярное ОВ направление в плоскости, перпендикулярной оси.

Из рис. 1 следует, что

F₂ = mg×sinj.

Здесь j –угловое отклонение мятника, отсчитываемое от положения равновесия. Угловое отклонение j можно рассматривать как вектор, лежащий на оси вращения, направление которого определяется направлением поворота тела из положения равновесия в заданное положение по правилу правого винта. Учитывая, что векторы 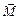и 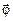антипараллельны, следует величинам проекций M и j на ось вращения приписать противоположные знаки.

Тогда формула (1) примет вид

M = -mgd sinj. (1.а)

При малых углах j можно ограничиться первым членом разложения функции sinj в ряд:

sinj = j - + -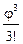

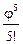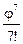
и принять sinj » j, если угол j выражен в радианах. Тогда формулу (1.а) можно записать следующим образом:

M = -mgdj. (2)

Используем основной закон динамики вращательного движения относительно неподвижной оси, записав его в проекциях на ось вращения:

М = Jb, (3)

где J – момент инерции тела относительно оси вращения; b – угловое ускорение, причем b = = .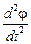

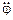Подставляя в формулу (3) выражение М из формулы (2), получим:

J 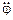+ mgdj = 0,

или

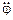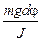+ = 0. (4)

Это линейное однородное дифференциальное уравнение второго порядка с постоянным коэффициентом, как известно, имеет решение

j(t) = j₀cos(w_Фt + a), (5)

содержащее две произвольные постоянные w_Ф и a, определяемые начальными условиями. Величины w_Ф и a называют соответственно амплитудой и начальной фазой колебаний. Заметим при этом, что циклическая частота физического маятника w_Ф, как и его период колебаний T_Ф, определяются динамическими свойствами системы и равны, соответственно,

w_Ф = 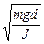и T_Ф = 2p 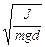, (6)

в чем можно убедиться, подставив решение j(t) в виде формулы (5) в уравнение (4).

Известно, что период колебаний математического маятника вычисляется по формуле

T_М =2p ,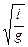

откуда следует, что математический маятник будет иметь тот же период колебаний, что и данный физический, если его длина равна

l_П = 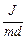. (7)

Это и есть формула приведённой длины физического маятника.