Модели пороговой чувствительности

ОСНОВНЫЕ ПОНЯТИЯ И РАСЧЁТНЫЕ ФОРМУЛЫ

СХЕМА СТРОЕНИЯ ГЛАЗА

Рис. взять из книги ЛУИЗОВА А. В. стр. 7

Схематический глаз человека

В глазе несколько преломляющих поверхностей, причем форма каждой отличается от сферической, а центры не лежат на одной прямой, т.е. система не центрирована. Однако для практических расчетов вполне можно принять, что поверхности являются сферическими, причём выбрана некоторая линия так, что центры всех сфер лежат в ней достаточно близко и её можно считать оптической осью глаза.

В таблице приложения 1 даны параметры схематического глаза по Гульстранду для покоя аккомодации и для максимальной аккомодации (фокусировка ближайшего предмета, который ещё можно ясно видеть).

Все расстояния отчитываются от вершины роговицы по направлению к сетчатке, радиусы кривизны – в том же направлении от сферической поверхности. Показатель преломления хрусталика различен в разных его точках. Он непрерывно возрастает от периферии к центру. Условно этому показателю в таблице приложения 1 придано только два значения- меньшее для поверхностной части ( в таблице хрусталик) и большее для внутренней (эквивалентное ядро хрусталика).

Редуцированный глаз

Наличие двух узловых точек в схематическом глазе по Гульстранду приводит к неудобствам построений и расчетов, Для многих расчётов две узловые точки сливаются в одну. При этом такой упрощенный глаз (редуцированный) обеспечивает вполне достаточную точность расчетов. В редуцированном глазе только одна преломляющая поверхность-роговица, и весь глаз наполнен однородной средой с одним показателем преломления. Поэтому обе узловые точки сливаются в одну, совпадающую с центром кривизны роговицы. Главные плоскости тоже сливаются в одну, и одна главная точка совпадает с вершиной роговицы. В таблице приложения 2 приведены данные редуцированного глаза по Вербицкому (для покоя аккомодации), наиболее близкие к данным глаза по Гульстранду.

В параксиальной области: ,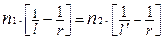

где 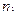, 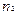- показатели преломления воздуха и стекловидного тела,

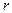- радиус кривизны роговицы,

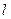-расстояние до объекта наблюдения,

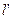- расстояние до изображения объекта.

Преломляющая сила оптики глаза .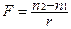

В редуцированном глазе аккомодация (приспособление глаза к изменяющемуся расстоянию до наблюдаемого объекта) учитывается следующим образом. По Вербицкому на каждую диоптрию добавочной рефракции показатель преломления глазной среды увеличивается на 0,0004, а радиус кривизны роговицы уменьшается на 0,004 мм. По Луизову при увеличении преломляющей силы на одну диоптрию радиус роговицы уменьшается на 0,1 мм.

Границы аккомодации глаза определяются ближней и дальней точками ясного видения. Ближняя точка ясного видения характеризуется наименьшим расстоянием от глаза наблюдателя до предмета, отчётливо различаемого при максимальной аккомодации. Дальняя точка ясного видения характеризуется расстоянием до наблюдаемого предмета, отчётливо видимого при полном покое аккомодационной мышцы.

Объём аккомодации (дптр) определяется по выражению ,

где 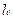- расстояние ближней точки от глаза, м;

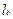- расстояние дальней точки от глаза, м.

Для глаза с нормальной рефракцией дальняя точка ясного видения расположена в бесконечности ( = - ∞).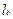

Объём аккомодации заметно зависит от возраста. На рисунке 3 представлена усреднённая зависимость объёма аккомодации от возраста.

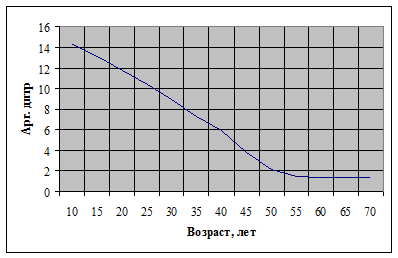
Рис. 2. Зависимость объёма аккомодации от возраста

При покое аккомодации эмметропический глаз фокусирует изображение удалённых предметов на сетчатке. Если же изображение удалённых предметов получается не на сетчатке, глаз называют аметропическим, а соответствующий недостаток его – аметропией. Аметропия характеризуется величиной обратной расстоянию дальней точки ясного видения. При миопии аметропия отрицательна, так как дальняя точка ясного видения расположена перед глазами. Для гиперметропа при покое аккомодации на сетчатке собрались бы лучи, сходящиеся в направлении некоторой точки, расположенной за сетчаткой и аметропия является положительной величиной.

Рефракция корректирующей линзы ,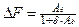

где 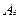- аметропия; δ – расстояние от задней главной точки корректирующей линзы до передней главной точки глаза.

Зрачковый рефлекс - уменьшение диаметра глазного зрачка по мере увеличения яркости поля зрения. Математическая зависимость диаметра зрачка от уровня яркости поля зрения, предложенная Крауфордом, имеет следующий вид

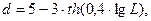
где d – диаметр зрачка, мм; L – яркость поля зрения, кд/м².

Данное уравнение с достаточной точностью определяет размер зрачка в том случае, если всё поле зрения или большая часть имеют одинаковую яркость. Увеличение поля зрения сверх 5- практически не оказывает влияния на зрачковый эффект.

Предельный угол разрешения, обусловленный дифракцией, равен

α=1,22λ⁄ ,

где α- предельный угол разрешения, рад;

λ – длина волны;

d- диаметр зрачка в тех же единицах длины, что и λ.

Освещённость сетчатки в зоне изображения объекта, лк

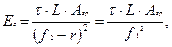
где τ – интегральный коэффициент пропускания глазных сред;

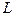– яркость объекта наблюдения;

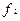- заднее фокусное расстояние оптической системы глаза;

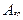- площадь зрачка;

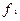- переднее фокусное расстояние оптической системы глаза.

Зависимость спектрального коэффициента пропускания глазных сред от длины представлена на рис.3. Значения приведены в таблице 4.

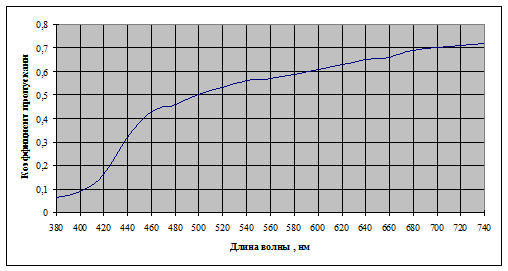
Рис. 3. Зависимость спектрального коэффициента пропускания глазных сред от длины волны

Освещённость сетчатки в троландах определяется произведением яркости объекта наблюдения на площадь зрачка , где 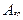- площадь зрачка, мм²; 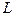– яркость объекта наблюдения, кд/м².

Относительная зрительная эффективность периферического пучка:

по Стайлсу-Крауфорду 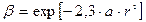, где 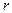- линейное смещение пучка от оптической оси, мм, 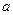- коэффициент, практически не меняющийся в условиях дневного зрения и принимаемый равным 0,05 мм 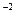для белого света;

по Муну и Спенсер .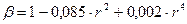

Эффективная освещённость сетчатки определяется яркостью объекта наблюдения и эффективной площадью зрачка, равной .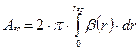

Относительное распределение освещённости сетчатки на границе изображения источника света описывается выражением:

,

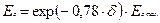где δ-угловое смещение от границы изображения, в минутах.

УСТАНОВИВШИЙСЯ ЗРИТЕЛЬНЫЙ ПРОЦЕСС

МОДЕЛИ ПОРОГОВОЙ ЧУВСТВИТЕЛЬНОСТИ

Высокопороговая модель Блэкуэлла

В данной модели порог - некая критическая точка в ряду множества значений стимула, в котором сигнал (стимул) вызывает ощущение. Если стимул не достиг этого критического значения, ощущение не возникает. Однако наличие ложных тревог (когда при отсутствии стимула испытуемый даёт положительный ответ), приводит к увеличению общего числа положительных ответов. Таким образом вероятность положительных ответов Р(Y/s) стимула s будет складываться из истинной вероятности обнаружения (без учёта угадывания) и вероятности успешного угадывания. Истинная вероятность обнаружения сигнала равна

Ри = [Р(Y/s)-P(Y/n)]/[1-P(Y/n)}, где Р(Y/s) - вероятность положительных ответов при предъявлении стимула; Р(Y/n) – ложных тревог.

Эта формула известна как формула поправки на случайный успех.

Зависимость вероятности обнаружения от значения стимула (психометрическая функция) в высокопороговой модели аппроксимируется кумулятивной кривой нормального распределения Гаусса. Порог определяется для заданной вероятности обнаружения с учетом поправки на случайный успех значением стимула, соответствующего этой вероятности.