Лекция 12. Уравнение поверхности и кривой в пространстве

Уравнением поверхности в пространстве Охуz называется уравнение F (х; у; z)= 0, которому удовлетворяют координаты каждой точки поверхности и только они.

Поверхность может, быть задана уравнением F (х; у; z)= 0(1), или, например, уравнением z = f (х; у)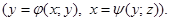

Уравнение вида F (х; у)= 0 (2) определяет в пространстве цилиндрическую поверхность с образующими параллельными оси Оz и направляющей, лежащей в плоскости Оху и заданной в ней уравнением F (х; у)= 0. Уравнение поверхности составляется по схеме составления уравнения линии на плоскости.

Кривую в пространстве можно рассматривать как линию пересечения двух поверхностей; тогда она задается системой двух уравнений 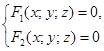(3)

Если кривую рассматривать как траекторию движения точки, то она задается параметрическими уравнениями х = х(t), у = y(t), z = z(t), t Î[a; b]. (4)

Поверхности второго порядка

Если в пространстве R³ ввести прямоугольную систему координат Охуz, то каждая поверхность определяется некоторым уравнением F (х, у, z) = 0, (х, у, z) –координаты любой точки поверхности. Если F (х, у, z) – многочлены не выше второй степени относительно совокупности переменных х, у, z, то уравнение F (х, у, z) = 0 называется уравнением второго порядка, а поверхность, изображаемая этим уравнением называется поверхностью второго порядка.

Если поверхность имеет специфическое расположение относительно системы координат (например, симметрична относительно некоторых координатных плоскостей, или имеет вершину в начале координат и пр.), то ее уравнение имеет достаточно простой вид, который называется каноническим.

Канонический вид уравнений поверхностей второго порядка. Геометрическое изображение

Сфера радиуса R с центром в начале координат x² + y² + z² = R².

Уравнение (х – х₀)² + (у – у₀)² + (z – z₀)² = R²изображает сферу радиуса R с центром в точке М₀ (х₀, у₀, z₀).

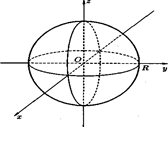
2) Эллипсоид с полуосями a, b, с и центром в начале координат

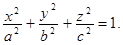
При а = b = с = R эллипсоид превращается в сферу радиуса R.

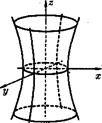3) Однополостный гиперболоид с полуосями а, b, с и осью Оz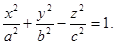

Сечения гиперболоида горизонтальными плоскостями z = h являются эллипсами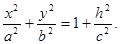

Сечения гиперболоида вертикальными плоскостями х = h являются гиперболами.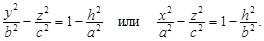

4) Двуполостный гиперболоид с полуосями а, b, с и осью Оz

Сечения гиперболоида горизонтальными плоскостями z = h, |h| > c являются эллипсами

Сечения гиперболоида вертикальными плоскостями х = h или y = h являются гиперболам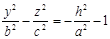и или

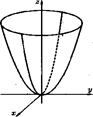5) Параболоид эллиптический с параметрами a, b, р и вершиной в начале координат 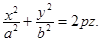Сечения параболоида горизонтальными плоскостями z = h, (h >0 при р > 0, h <0 при р < 0) есть эллипсы

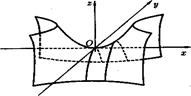Сечения параболоида вертикальными плоскостями х = h или у = h являются параболами.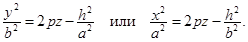

6) Параболоид гиперболический с параметрами а, b, р и вершиной в начале координат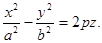

Сечения параболоида горизонтальными плоскостями z = h представляют собой гиперболы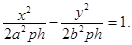

Сечения вертикальными плоскостями х = h и у = h являются параболами

7) Конус эллиптический с вершиной в начале координат и осью Оz Если а = b, то конус круглый или круговой. Пересечение горизонтальными плоскостями являются эллипсами 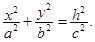(при h = 0 эллипс вырождается в точку). Сечения конуса вертикальными плоскостями х = h и y = h гиперболами при 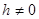или парой пересекающих прямых и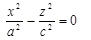

К поверхностям второго порядка относятся цилиндры, направляющие которых – линии второго порядка. Мы ограничимся перечислением цилиндров, направляющие которых расположены в плоскости Оху, а образующие – прямые, параллельные оси Оz.

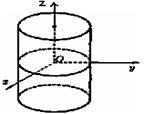8) Цилиндры: (1) Эллиптический Если а = b = R, то цилиндр – круговой х² + у² = R.

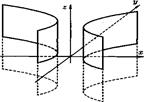
(2) Гиперболический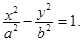

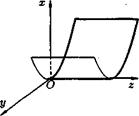
(3) Параболический у² = 2рх.

Метод параллельных сечений

Если задано уравнение той или иной поверхности, то возникает задача исследования ее формы и расположения относительно координатных осей. Для решения этой задачи обычно применяют метод параллельных сечений: поверхность пересекается несколькими плоскостями, параллельными плоскостям координат. Форма и размер полученных сечений позволяют выяснить геометрическую форму самой поверхности.

Пересечение поверхности с плоскостью

Линию в пространстве R³ можно определить как пересечение двух поверхностей. Таким образом уравнение линии можно записать в виде системы 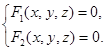Для исследования этой линии удобно воспользоваться цилиндром, проектирующем ее на ту или иную координатную плоскость. Если, например, проектируем линию на плоскость Оху, то исключим z из системы и получим уравнение j (х, у) = 0. Оно изображает направляющую проектирующего цилиндра на плоскость Оху. В зависимости от того, будет ли j (х, у) = 0 эллипсом, гиперболой, параболой, парой прямых – изучаемая линия сохранит соответствующее название.