Площадь криволинейного сектора

Пусть кривая 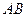в полярных координатах задана урав -нением , где функция положи -тельна и непрерывна на отрезке 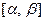. Фигуру, ограниченную двумя лучами, образующими с полярной осью углы 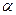и 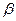, и кривой 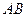, называют криволинейным сектором. Площадь криволинейного сектора ищется по формуле:

(3)

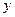
x

Например, Найти площадь кардиоиды .

y

a

2a 0 x

Длина дуги кривой.

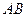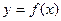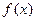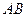а) Пусть плоская кривая задана уравнением на отрезке где непрерывна вместе со своей производной на отрезке тогда длина дуги вычисляется по формуле:

. (4)

ПРИМЕР. Найти длину кривой на отрезке

. По формуле (4),

ЗАМЕЧАНИЕ 1. В случае, если дуга 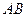задана парамет -рическими уравнениями; , причём , в формуле (4) можно сделать замену переменной: .

Получим:

или . (5)

ПРИМЕР: Найти длину дуги кривой, заданной параметри -ческими уравнениями:

Тогда

ЗАМЕЧАНИЕ 2. Для вычислении длины дуги в случае, ког- да кривая 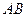задана в полярных координатах уравнением применяется следующая формула:

(6)

ПРИМЕР: найти длину дуги кривой , если .

Тогда

4. Объём тела вращения.

Пусть функция 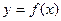непрерывна и неотрицательна на отрезке . Тогда объём тела, образованного вращением вокруг оси 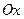криволинейной трапеции, ограничен- ной сверху графиком функции 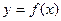, можно найти по формуле:

(7)

ПРИМЕР: Найти объём тела, образованного вращением вокруг оси 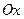фигур, ограниченных графиками функций:

y

1 x

Объём полученного тела находим следующим образом

Симметричная формула получается для вычисления объё -ма тела, образованного вращением некоторой фигуры вокруг оси

(8)

ПРИМЕР. Найти объём тела ,образованного вращением вокруг оси фигуры, ограниченной линиями

y

1 2

Найдём объём полученного тела. Найдём пересечение линий, ограничивающих область: при . Тогда ,

. Если то . Тогда

§ 4. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ.

Когда вводится определённый интеграл как предел инте -гральных сумм, обычно предполагается, что подынтегральная функция ограничена на отрезке и сам отрезок конечный. Если отказаться от этих условий, получим некоторые обобщения оп- ределённого интеграла, так называемые несобственные инте –гралы 1 – го и 2 – го рода.

1. Несобственный интеграл 1 го рода ( с бесконечными пределами интегрирования). Пусть функция 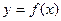опре -делена на промежутке и интегрируема на любом конечном промежутке при любом . Тогда, если существует конечный предел , то он называется несобственным интегралом 1 – го рода и обозначается

и интеграл при этом называется сходящимся; если же такой предел не существует или бесконечный, то интеграл называ- ется расходящимся.

Аналогично можно определить:

и

ПРИМЕРЫ:

1.

Следовательно, данный интеграл сходится.

2.

Следовательно, интеграл сходится.

3.

Следовательно, данный интеграл расходится.

2.Несобственный интеграл 2 – го рода (от неограни -ченных функций).

Пусть функция 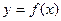определена на отрезке Точка называется особой точкой, если функция неогра- ниченна в любой окрестности этой точки, но ограничена на любом отрезке . Если при любом существует определённый интеграл и существует конечный предел при таких интегралов, то этот пре -дел называют несобственным интегралом 2 – го рода и обо- значают

Аналогично, если 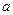- особая точка, то

и, если особой точкой является некоторая точка , то

Если данные пределы существуют и конечны, то соответст -вующие интегралы 2 – го рода называются сходящимися. Если же данные пределы не существуют илибесконечны, то соот -ветствующие несобственные интегралы называются расходя – щимися..

ПРИМЕРЫ.

1.

( - особая точка )=

поэтому интеграл сходится.

Следовательно, данный несобственный интеграл расходится.