Применение производной к исследованию функций
Теоремы Ферма, Ролля, Лагранжа. Возрастание и убывание функций. Понятие экстремума, необходимое условие экстремума. Наибольшее и наименьшее значения функций.
Выпуклость вверх, вниз; точки перегиба. Достаточные условия выпуклости. Достаточные условия экстремума.
Асимптоты функций. Общая схема исследования функции и построения ее графика..
Теорема Коши, обобщенная теорема Коши. Правило Лопиталя раскрытия неопределенностей.
Формула Тейлора. Разложение по степеням x функций 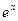 ,
, 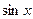 ,
, 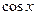 ,
, 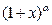 ,
, 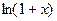 . Некоторые применения формулы Лагранжа о среднем и формулы Тейлора.
. Некоторые применения формулы Лагранжа о среднем и формулы Тейлора.
5. Неопределенный интеграл
Первообразная. Неопределенный интеграл и его свойства. Таблица основных интегралов. Теорема о замене переменной. Примеры использования формулы замены переменной. Вторая теорема о замене переменной (подстановка). Вычисление интегралов 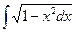 ,
, 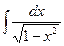 ,
, 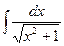 ,
, 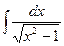 . Теорема об интегрировании по частям. Примеры использования формулы интегрирования по частям. Вычисление интегралов
. Теорема об интегрировании по частям. Примеры использования формулы интегрирования по частям. Вычисление интегралов 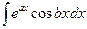 ,
, 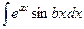 ,
, 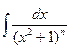 . Обобщенная формула интегрирования по частям.
. Обобщенная формула интегрирования по частям.
Полярная запись векторов плоскости. Определение умножения векторов в полярной записи, координатная запись произведения. Свойства умножения. Поле комплексных чисел. Изоморфное вложение поля действительных чисел в поле комплексных чисел. Операция комплексного сопряжения. Правило деления комплексных чисел. Формула корней n-й степени из комплексного числа. Корни n-й степени из 1 и их расположение на плоскости.
Многочлены, сложение и умножение многочленов. Теорема о делении многочленов с остатком. Корни многочленов. Теорема Безу и следствия из нее. Кратные корни. Формулировка основной теоремы алгебры; следствия из нее. Теорема Виета. Теорема о корнях многочленов с действительными коэффициентами.
Разложение дробно-рациональной функции на сумму правильных дробей. Теорема о разложении дробно-рациональной функции на сумму простейших дробей над полем C. Формулировка теоремы о разложении дробно-рациональной функции на сумму простейших дробей над полем R.
Интегрирование простейших рациональных дробей − нахождение интегралов 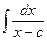 ,
, 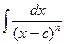 ,
, 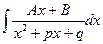 ,
, 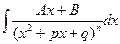 , где
, где 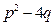 <0,
<0, 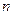 >1.
>1.
6. Простейшие дифференциальные уравнения
Некоторые задачи, приводящие к обыкновенным дифференциальным уравнениям. Дифференциальные уравнения первого порядка. Понятие об общем, частном и особом решениях дифференциальных уравнений.
Основные классы дифференциальных уравнений первого порядка, интегрируемых в квадратурах: Уравнения в полных дифференциалах, с разделяющимися переменными, линейные, однородные, уравнение Бернулли.
