Преобразование лапласа

Выпишем прямое и обратное преобразование Фурье. 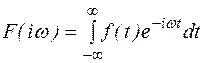(1)

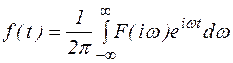(2)

В соответствии с приведенной теоремой функция f(t) преобразуется по Фурье если:

1) f(t) – кусочно – непрерывная кусочно – дифференцируемая функция.

2) f(t) удовлетворяет условию абсолютной интегрируемости, т. е.

.

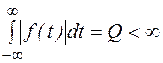Большинство элементарных функций не удовлетворяют условию абсолютной интегрируемости и, следовательно, не преобразуются по Фурье. Однако с помощью простых преобразований можно обобщить преобразование Фурье на многие функции. Поступают так. Функцию f(t) умножают на 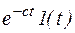, где с подбирают так, чтобы обеспечить абсолютную интегрируемость. Запишем условие абсолютной интегрируемости для функции:

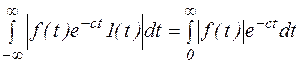
Наименьшее из чисел с или предел к которому стремится с, для которых

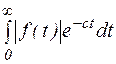- существует (конечен) называется абсциссой абсолютной сходимости и обозначается .

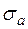Запишем 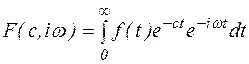, 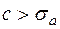(3)

Равенство (3) задает одностороннее преобразование Фурье. В соответствии с (2) обратное одностороннее преобразование Фурье задается равенством:

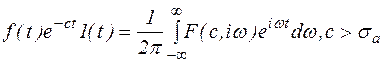(4)

При переходе от преобразования Фурье к одностороннему преобразованию Фурье уменьшается интервал определения функции f(t), которая теперь определена в области 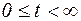. Такое усечение интервала определения с физической точки зрения оправдывается тем, что в технических системах все процессы имеют начало, момент начала которого можно совмести с точкой 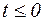. Объединим в одностороннем преобразовании (3) множитель 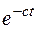с ядром преобразования 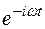: 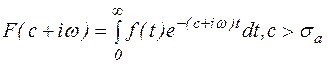(5)

Равенство (5) задает обобщенное преобразование Фурье. Оно позволяет по вещественной функции f(t) построить комплексную функцию F(с+iw). Найдем преобразование обратное к преобразованию Фурье. Перепишем (4) в виде:

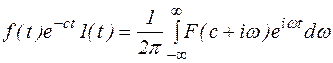(6)

Умножим (6) на :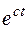

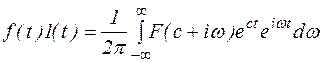
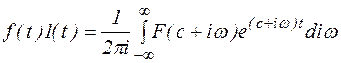
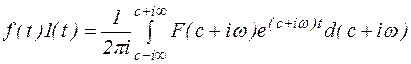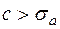, (7) – позволяет по комплексной функции F(c+iw) восстановить вещественную функцию f(t) и называется обратным обобщенным преобразованием Фурье.

Введем комплексную переменную s=c+iw, тогда равенства (5) и (7) принимают вид:

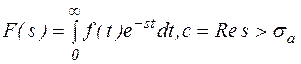(8)

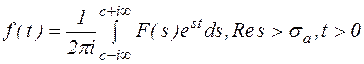(9)

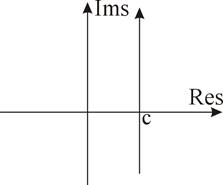Равенства (8) и (9) задают соответственно прямое и обратное преобразование Лапласа. В равенстве (9) пределы интегрирования показывают, что интегрирование ведется вдоль прямой Res=c.

Рис.1

В преобразовании Лапласа функцию f(t) называют оригиналом, а функцию F(s) – изображением.

Символически преобразование Лапласа записывается в виде :

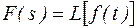
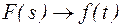
Для обратного преобразования используется соотношение:

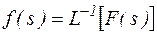
Преобразование Лапласа позволяет перейти от оригинала к изображению. Переход от оригинала к изображению позволяет упростить ряд математических операций, в том числе решение линейных дифференциальных уравнений.