Задачи для самостоятельного решения. Найти общее (частное) решение уравнения
Найти общее (частное) решение уравнения
9.1. 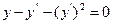 .
.
9.2. 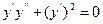 .
.
9.3. 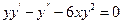 ;
; 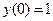 ,
, 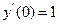 .
.
9.4. 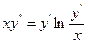 .
.
9.5. 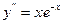 ,
, 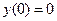 ,
, 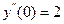 .
.
Ответы:
9.1. 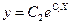 ;
;
9.2. 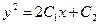 ;
;
9.3. 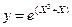 ;
;
9.4. 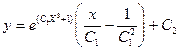 ;
;
9.5. 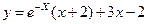 .
.
Контрольные вопросы.
1.Какое дифференциальное уравнение называется уравнением 2-го, n-го порядка? Приведите примеры.
2.Как определяются общее и частное решения уравнения 2-го, n-го порядка? Запишите общий вид этих решений.
3.Способы решения уравнений, допускающих понижение порядка, перечислите их. Приведите примеры.
Cправочная таблица 2
| Алгоритм решения уравнения | Тип уравнения | Признак типа | Метод понижения порядка |
1. Определить тип уравнения. 2. Понизить порядок уравнения. 3. Решить полученное уравнение 1-го порядка (см.табл.1.) относительно функции z или p. 4. Возвратиться к первоначальной переменной, заменив z(x) или p(y) на 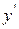 . 5.Решить вновь полученное уравнение 1-го порядка с разделяющимися переменными. . 5.Решить вновь полученное уравнение 1-го порядка с разделяющимися переменными. | 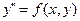 | Нет явно 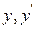 | Последовательное интегрирование два раза |
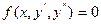 | Нет явно y | Ввести подстановку: y=z(x), 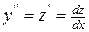 | |
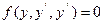 | Нет явно x | Ввести подстановку: 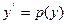 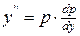 |
10. Линейные дифференциальные уравнения 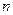 -ого порядка.
-ого порядка.
Определение 10.1: Линейнымдифференциальным уравнением п-го порядка называется уравнение вида
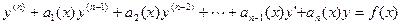 (10.1)
(10.1)
Здесь функции 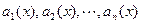 ) и
) и 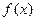 заданы и непрерывны в некотором промежутке
заданы и непрерывны в некотором промежутке 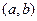 .
.
Уравнение (1) называется линейным неоднородным, или уравнением с правой частью. Если же 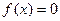 , то уравнение называется линейным однородным. Однородное уравнение с той же левой частью, что и данное неоднородное, называется соответствующим ему.
, то уравнение называется линейным однородным. Однородное уравнение с той же левой частью, что и данное неоднородное, называется соответствующим ему.
Рассмотрим линейные однородные уравнения.: общее решение таких уравнений можно найти по их известным частным решениям.
Теорема: (Теорема о структуре общего решения линейного однородного уравнения)
Если 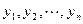 — линейно независимые частные решения уравнения
— линейно независимые частные решения уравнения
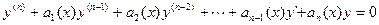
то 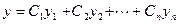 есть общее решение этого уравнения (
есть общее решение этого уравнения ( 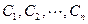 —произвольные постоянные).
—произвольные постоянные).
Примечание. Функции 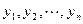 называются линейно независимыми в промежутке
называются линейно независимыми в промежутке 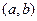 если они не связаны никаким тождеством
если они не связаны никаким тождеством
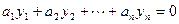
где 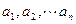 какие-нибудь постоянные, не равные нулю одновременно.
какие-нибудь постоянные, не равные нулю одновременно.
Для случая двух функций это условие можно сформулировать и так: две функции 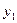 и
и 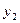 линейно независимы, если их отношение не является постоянной величиной :
линейно независимы, если их отношение не является постоянной величиной : 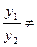 const. Например:
const. Например:
1) 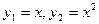 —линейно независимы;
—линейно независимы;
2) 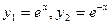 —линейно независимы;
—линейно независимы;
3) 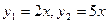 — линейно зависимы.
— линейно зависимы.
Совокупность 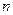 решений линейного однородного уравнения
решений линейного однородного уравнения 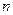 -го порядка, определенных и линейно независимых в промежутке
-го порядка, определенных и линейно независимых в промежутке 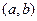 , называется фундаментальной системой решений этого уравнения.
, называется фундаментальной системой решений этого уравнения.
Для линейного однородного дифференциального уравнения второго порядка
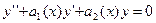
фундаментальная система состоит из двух линейно независимых решений 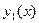 и
и 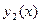 его общее решение находится по формуле
его общее решение находится по формуле