Краткие сведения из теории вероятностей и математической статистики

Под случайной величиной X понимается величина, которая в результате измерения (опыта) со случайным исходом принимает то или иное значение из некоторого интервала.

Плотностью распределения непрерывной случайной величины Х называется функция, описывающая вероятность распределения случайной величины на числовой прямой.

Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных ее значений на вероятности этих значений.

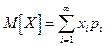
Перейдем от дискретной случайной величины Х к непрерывной с плотностью f(x).

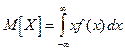
Дисперсия случайной величины есть математическое ожидание квадрата соответствующей центрированной величины:

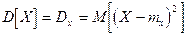
Для непосредственного вычисления дисперсии непрерывной случайной величины служит формула:

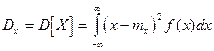
В качестве меры рассеяния также используется среднеквадратическое отклонение величины

.

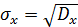Под случайной выборкой объема n понимают совокупность случайных величин, не зависимых между собой.

Упорядоченной статистической совокупностью будем называть случайную выборку, величины в которой расположены в порядке возрастания.

Группированным статистическим рядом называются интервалы с соответствующими им частотами, на которые разбивается упорядоченная выборка, причем ширина интервала находится, как

,

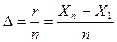где r – размах выборки.

Тогда частоту попадания величины в отрезок 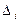находим по формуле

,

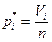где V_i - число величин попавших в отрезок 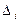, причем 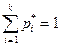. Поделив каждую частоту на 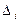, получим высоту для построения гистограммы.

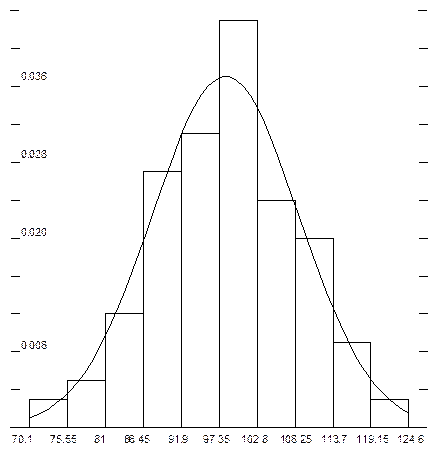
Рис. 1 Пример гистограммы и графика плотности распределения

случайной величины.

Построив гистограмму, мы получили аналог кривой распределения, по которой можем выдвинуть гипотезу о законе распределения. Для выравнивания статистического распределения с помощью закона, о котором выдвинули гипотезу, нужно статистическое среднее (оценка математического ожидания) m_x^* и статистическая дисперсия (оценка дисперсии) D_x^*.

Находим их как

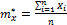
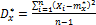
Плотность распределения случайной величины характеризует закон распределения случайной величины. Существуют различные законы распределения: равномерный закон распределения (закон равномерной плотности), закон Пуассона, нормальный закон, закон Эрланга и т.д.

Наиболее часто встречающийся на практике закон распределения - нормальный. Плотность распределения описывается формулой

.

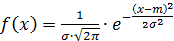Вероятность попадания случайной величины в интервал от a до b определяется зависимостью

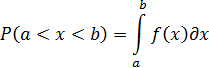
или, используя т.н. функцию Лапласа ( 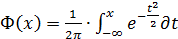), значения которой табулированы,

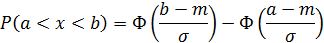
Для нормально распределенной случайной величины все рассеяние с точностью до 1% укладывается в интервале .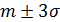

Нормальный закон описывает распределение случайной величины на интервале от 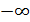до 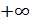. Однако, как правило, интервал распределения случайной величины ограничен конкретными значениями величины a и b. В таком случае используется усеченный нормальный закон распределения 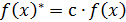, отличающийся множителем – нормирующим коэффициентом, который определяется по зависимости

.

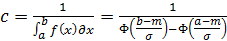Выше рассматривалась вероятность попадания случайной величины X в заданный неслучайный интервал (a,b). Если повернуть ситуацию иначе: величина X не случайна, зато случаен интервал (a,b). Случайно его положение на оси абсцисс, определяемое его центром m, случайна длина интервала. Вероятность того, что случайный интервал (a,b) накроет точку X, называется доверительной вероятностью. А сам интервал – доверительным интервалом. Границы интервала называются доверительными границами.

Дерево исходов

Пусть в результате некоторого эксперимента возможны различные исходы. Будем предполагать, что ни один из исходов w₁, w₂, ... , w_n нельзя представить в виде комбинации остальных (как говорят, w₁, w₂, ... , w_n неразложимы).

Неразложимые исходы w₁, w₂, ... , w_n некоторого эксперимента будем называть элементарными событиями, а их совокупность

W={w₁, w₂, ... , w_n} (конечным) пространством элементарных событий или пространством исходов.

Обычно интересуются не тем, какой конкретно исход имеет место в результате испытания, а тем, принадлежит ли исход тому или иному подмножеству всех исходов. Все те подмножества А, для которых по условиям эксперимента возможен ответ одного из двух типов: «исход w Î A» или «исход w Ï A», будем называть событиями.

Вероятностью P(A) события A называется число, равное отношению числа |A| элементарных исходов, составляющих A, к числу |W| всех элементарных и равновозможных исходов.

Свойства вероятностей

1) 0 £ P(A) £ 1;

2) P(A) = 0 тогда и только тогда, когда A = Æ – невозможное событие;

3) P(A) = 1 тогда и только тогда, когда A = W – достоверное событие;

4) P(A + B) = P(A) + P(B), если A•B = Æ (A, B – несовместные события);

5) P(A + B) = 1, если B – событие, противоположное A.

Пример 1 (задача Гюйгенса). В урне два белых и четыре черных шара. Один азартный человек держит пари с другим, что среди вынутых трех шаров будет ровно один белый. В каком отношении находятся шансы спорящих?

Решение 1 (традиционное). В данном случае испытание W = {вынимание трех шаров}, а событие A – благоприятствующее одному из спорящих:

A = {достать ровно один белый шар}.

Поскольку порядок вынимания трех шаров не важен, то число всех исходов | W | находим как число сочетаний из 6 по 3, т. е.

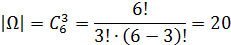
Один белый шар можно достать в 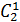, случаях, а два черных – в 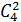, и тогда по основному правилу комбинаторики .

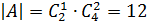Отсюда 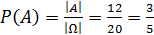, а по пятому свойству вероятности

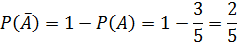
Следовательно,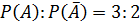

Граф – это два непустых множества, элементы первого называются вершинами, а второго – ребрами. Каждое ребро соединяет не более двух вершин и любую пару вершин соединяет не более чем одно ребро.

Граф связный, если из любой вершины в любую другую можно пройти по ребрам.

Циклом называется замкнутый путь из ребер, а деревом – связный граф без циклов.

Граф называется вероятностным, если рядом с каждым ребром графа исходов некоторого испытания записать вероятность события, соответствующего начальной вершине ребра (ориентация ребер задается, например, на дереве, расстоянием от его корня).

Теорема сложения.Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного наступления:

P(A + B) = P(A) + P(B) – P(A•B).

Условной вероятностью 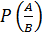события A при условии, что событие B произошло (P(B) ¹ 0), назовем отношение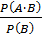

Это определение эквивалентно так называемой теореме умножения, согласно которой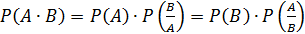

т.е. вероятность произведения двух событий равна вероятности одного из них, умноженной на условную вероятность другого при условии, что первое событие произошло.

Решение 2. Составим вероятностное дерево исходов

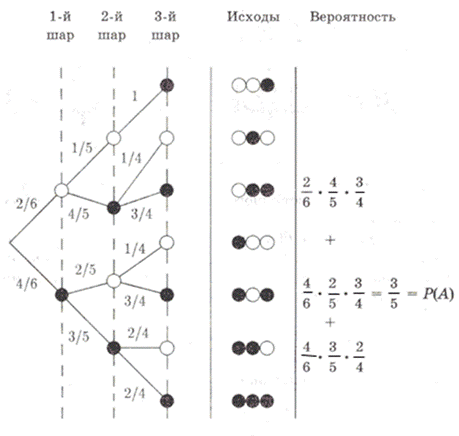
Рис. 2 Вероятностное дерево исходов.

В этом решении использовалось понятие вероятностного графа.

Эксперимент

Важнейшей составной частью научных исследований является эксперимент, основой которого является научно поставленный опыт с точно учитываемыми и управляемыми условиями.

Само слово «эксперимент» происходит от латинского «experimentum» - проба, опыт.

В это понятие вкладывается научная постановка опытов и наблюдение исследуемого явления в точно учитываемых условиях, позволяющих следить за ходом явлений и воссоздавать его каждый раз при повторении этих условий.

Основной целью эксперимента являются выявление свойств исследуемых объектов, проверка справедливости гипотез и на этой основе широкое и глубокое изучение темы научного исследования.

Постановка и организация эксперимента определяются его назначением.

Эксперименты различаются

по способу формирования условий: естественные и искусственные;

по целям исследования: преобразующие, констатирующие, контролирующие, поисковые, решающие;

по организации проведения: лабораторные, натурные, полевые, производственные и т.п.;

по структуре изучаемых объектов и явлений: простые, сложные;

по характеру внешних воздействий на объект исследования: вещественные, энергетические, информационные;

по характеру взаимодействия средства экспериментального исследования с объектом исследования: обычный и модельный;

по типу моделей, исследуемых в эксперименте: материальный и мысленный;

по контролируемым величинам: пассивный и активный;

по числу варьируемых факторов: однофакторный и многофакторный;

по характеру изучаемых объектов или явлений: технологические, социометрические и т.п.

Для классификации могут быть использованы и другие признаки.

Естественный эксперимент предполагает проведение опытов в естественных условиях существования объекта исследования (чаще всего используется в биологических, социальных, педагогических и психологических науках).

Искусственный эксперимент предполагает формирование искусственных условий (широко применяется в естественных и технических науках).

Преобразующий (созидательный) эксперимент включает активное изменение структуры и функций объекта исследования в соответствии с выдвинутой гипотезой, формирование новых связей и отношений между компонентами объекта или между исследуемым объектом и другими объектами. Исследователь в соответствии со вскрытыми тенденциями развития объекта исследования преднамеренно создает условия, которые должны способствовать формированию новых свойств и качеств объекта.

Констатирующий эксперимент используется для проверки определенных предположений. В процессе этого эксперимента констатируется наличие определенной связи между воздействием на объект исследования и результатом, выявляется наличие определенных фактов.

Контролирующий эксперимент сводится к контролю за результатами внешних воздействий на объект исследования с учетом его состояния, характера воздействия и ожидаемого эффекта.

Поисковый эксперимент проводится в том случае, если затруднена классификация факторов, влияющих на изучаемое явление вследствие отсутствия достаточных предварительных (априорных) данных. По результатам поискового эксперимента устанавливается значимость факторов, осуществляется отсеивание незначимых.

Решающий эксперимент ставится для проверки справедливости основных положений фундаментальных теорий в том случае, когда две или несколько гипотез одинаково согласуются со многими явлениями. Это согласие приводит к затруднению, какую именно из гипотез считать правильной.

Решающий эксперимент дает такие факты, которые согласуются с одной из гипотез и противоречат другой.

Примером решающего эксперимента служат опыты по проверке справедливости ньютоновской теории истечения света и волнообразной теории Гюйгенса. Эти опыты были поставлены французским ученым Фуко (1819-1868). Они касались вопроса о скорости распространения света внутри прозрачных тел. Согласно гипотезе истечения, скорость света внутри таких тел должна быть больше, чем в пустоте. Но Фуко своими опытами доказал обратное, т.е. что в менее плотной среде скорость света большая. Этот опыт Фуко и был тем решающим опытом, который решил спор между двумя гипотезами (в настоящее время гипотеза Гюйгенса заменена электромагнитной гипотезой Максвелла).

Другим примером решающего эксперимента может служить спор между Птолемеем и Коперником о движении Земли. Решающий опыт Фуко с маятником окончательно решил спор в пользу теории Коперника.

Лабораторный эксперимент проводится в лабораторных условиях с применением типовых приборов, специальных моделирующих установок, стендов, оборудования и т.д. Чаще всего в лабораторном эксперименте изучается не сам объект, а его образец. Этот эксперимент позволяет доброкачественно, с требуемой повторностью изучить влияние одних характеристик при варьировании других, получить хорошую научную информацию с минимальными затратами времени и ресурсов. Однако такой эксперимент не всегда полностью моделирует реальный ход изучаемого процесса, поэтому возникает потребность в проведении натурного эксперимента.

Натурный эксперимент проводится в естественных условиях и на реальных объектах. Этот вид эксперимента часто используется в процессе натурных испытаний изготовленных систем. В зависимости от места проведения испытаний натурные эксперименты подразделяются на производственные, полевые, полигонные, полунатурные и т.п. Практически во всех случаях основная научная проблема натурного эксперимента - обеспечить достаточное соответствие (адекватность) условий эксперимента реальной ситуации, в которой будет работать впоследствии создаваемый объект.

Центральными задачами натурного эксперимента являются:

- изучение характеристик воздействия среды на испытуемый объект;

- идентификация статистических и динамических параметров объекта;

- оценка эффективности функционирования объекта и проверка его на соответствие заданным требованиям.

Эксперименты могут быть открытыми и закрытыми, они широко распространены в психологии, социологии, педагогике. В открытом эксперименте его задачи открыто объясняются испытуемым, в закрытом - в целях получения объективных данных эти задачи скрываются от испытуемого.

Простой эксперимент используется для изучения объектов, не имеющих разветвленной структуры, с небольшим количеством взаимосвязанных и взаимодействующих элементов, выполняющих простейшие функции.

В сложном эксперименте изучаются явления или объекты с разветвленной структурой (можно выделить иерархические уровни) и большим количеством взаимосвязанных и взаимодействующих элементов, выполняющих сложные функции. Высокая степень связности элементов приводит к тому, что изменение состояния какого-либо элемента или связи влечет за собой изменение состояния многих других элементов системы. В сложных объектах исследования возможно наличие нескольких разных структур, нескольких разных целей.

Информационный эксперимент используется для изучения воздействия определенной (различной по форме и содержанию) информации на объект исследования (чаще всего информационный эксперимент используется в биологии, психологии, социологии, кибернетике и т.п.). С помощью этого эксперимента изучается изменение состояния объекта исследования под влиянием сообщаемой ему информации.

Вещественный эксперимент предполагает изучение влияния различных вещественных факторов на состояние объекта исследования. Например, влияние различных добавок на качество стали и т.п.

Энергетический эксперимент используется для изучения воздействия различных видов энергии (электромагнитной, механической, тепловой и т.д.) на объект исследования. Этот тип эксперимента широко распространен в естественных науках.

Обычный (или классический) эксперимент включает экспериментатора как познающего субъекта; объект или предмет экспериментального исследования и средства (инструменты, приборы, экспериментальные установки), при помощи которых осуществляется эксперимент. В обычном эксперименте экспериментальные средства непосредственно взаимодействуют с объектом исследования. Они являются посредниками между экспериментатором и объектом исследования.

Модельный эксперимент в отличие от обычного имеет дело с моделью исследуемого объекта. Модель входит в состав экспериментальной установки, замещая не только объект исследования, но часто и условия, в которых изучается некоторый объект. Модельный эксперимент при расширении возможностей экспериментального исследования одновременно имеет и ряд недостатков, связанных с тем, что различие между моделью и реальным объектом может стать источником ошибок и, кроме того, экстраполяция результатов изучения поведения модели на моделируемый объект требует дополнительных затрат времени и теоретического обоснования правомочности такой экстраполяции.

Различие между орудиями эксперимента при моделировании позволяет выделить мысленный и материальный эксперимент.

Орудиями мысленного (умственного) эксперимента являются мысленные модели исследуемых объектов или явлений (чувственные образы, образно-знаковые модели, знаковые модели). Для обозначения мысленного эксперимента иногда пользуются терминами: идеализированный или воображаемый эксперимент.

Структура мысленного эксперимента включает: построение мысленной модели объекта исследования, идеализированных условий эксперимента и воздействий на объект; сознательное и планомерное изменение, комбинирование условий эксперимента и воздействий на объект; сознательное и точное применение на всех стадиях эксперимента объективных законов науки, благодаря чему исключается абсолютный произвол. В результате такого эксперимента формируются выводы.

Материальный эксперимент имеет аналогичную структуру. Однако в материальном эксперименте используются материальные, а не идеальные объекты исследования. Основное отличие материального эксперимента от мысленного в том, что реальный эксперимент представляет собой форму объективной материальной связи сознания с внешним миром, между тем как мысленный эксперимент является специфической формой теоретической деятельности субъекта.

Пассивный эксперимент предусматривает измерение только выбранных показателей (параметров, переменных) в результате наблюдения за объектом без искусственного вмешательства в его функционирование.

Примерами пассивного эксперимента является наблюдение: за интенсивностью, составом, скоростями движения транспортных потоков; за числом заболеваний вообще или какой-либо определенной болезнью; за работоспособностью определенной группы лиц; за показателями, изменяющимися с возрастом; за числом дорожно-транспортных происшествий и т.п.

Пассивный эксперимент, по существу, является наблюдением, которое сопровождается инструментальным измерением выбранных показателей состояния объекта исследования.

Активный эксперимент связан с выбором специальных входных сигналов (факторов) и контролирует вход и выход исследуемой системы.

Однофакторный эксперимент предполагает: выделение нужных факторов; стабилизацию мешающих факторов; поочередное варьирование интересующих исследователя факторов.

Стратегия многофакторного эксперимента состоит в том, что варьируются все переменные сразу и каждый эффект оценивается по результатам всех опытов, проведенных в данной серии экспериментов.

Для проведения эксперимента любого типа необходимо:

1) разработать гипотезу, подлежащую проверке;

2) создать программы экспериментальных работ;

3) определить способы и приемы вмешательства в объект исследования;

4) обеспечить условия для осуществления процедуры экспериментальных работ;

5) разработать пути и приемы фиксирования хода и результатов эксперимента;

6) подготовить средства эксперимента (приборы, установки, модели и т.п.);

7) обеспечить эксперимент необходимым обслуживающим персоналом.

Особое значение имеет правильная разработка методик эксперимента.

Методика эксперимента - это совокупность операций, выполняемых в определенной последовательности, в соответствии с которой достигается цель исследования.

При разработке методик проведения эксперимента необходимо предусматривать:

проведение предварительного целенаправленного наблюдения над изучаемым объектом или явлением с целью определения исходных данных (гипотез, выбора варьирующих факторов);

создание условий, в которых возможно экспериментирование (подбор объектов для экспериментального воздействия, устранение влияния случайных факторов);

определение пределов измерений; систематическое наблюдение за ходом развития изучаемого явления и точные описания фактов;

проведение систематической регистрации измерений и оценок фактов различными средствами и способами;

создание повторяющихся ситуаций, изменение характера условий и перекрестные воздействия, создание усложненных ситуаций с целью подтверждения или опровержения ранее полученных данных;

переход от эмпирического изучения к логическим обобщениям, к анализу и теоретической обработке полученного фактического материала.

Перед каждым экспериментом составляется его план (программа), который включает: цель и задачи эксперимента; выбор варьирующих факторов; обоснование объема эксперимента, числа опытов; порядок реализации опытов, определение последовательности изменения факторов; выбор шага изменения факторов, задание интервалов между будущими экспериментальными точками; обоснование средств измерений; описание проведения эксперимента; обоснование способов обработки и анализа результатов эксперимента.

Результаты экспериментов должны отвечать трем статистическим требованиям:

требование эффективности оценок, т.е. минимальность дисперсии отклонения относительно неизвестного параметра;

требование состоятельности оценок, т.е. при увеличении числа наблюдений оценка параметра должна стремиться к его истинному значению;

требование несмещенности оценок - отсутствие систематических ошибок в процессе вычисления параметров.

Итак, эксперимент включает в себя несколько этапов: организация эксперимента или подготовка условий проведения опытов, включая планирование, выбор методики, средств измерений и пр., ход эксперимента (проведение опытов), получение результатов, обработка и анализ результатов.