Практическая работа 14

Построение графиков функции с помощью производной.

Цель работы

Научиться исследовать функцию с помощью производной и строить по результатам исследования график

Ход работы

Вариант

Исследовать функцию и построить её график:

2.1.1

2.1.2

2.1.3

2.1.4

Изм.

Лист

№ докум.

Подпись

Дата

Лист

ПР. .00.00

2.2. Допуск к работе

2.2.1 Заполните пропуски

А) Если производная дифференцируемой функции положительна на промежутке, то функция на этом промежутке _____________________.

Б) Если производная дифференцированной функции _________________ на промежутке, то функция на этом промежутке убывает.

В) Если для дважды дифференцируемой функции вторая её производная отрицательнавнутри промежутка, то график функции является ______________ на данном промежутке.

Г) Если же вторая производная __________________ внутри промежутка, то график функции является вогнутым на данном промежутке.

2.2.2 Заполните пропуски

Схема исследования функции

1. Найдите область определения функции.

2. Определите четность, нечетность функции. ( f(-x) = f(x) - ____________________

f(-x) = __________ - нечётная)

3 Найти точки пересечения графика функции с осями координат. ( с осью ОХ у = ___ , с осью _____ х = 0).

4. Найдите производную функции.

5. Определите стационарные и критические точки производной. Т. е. точки в которых производная равна ________ и не существует.

6.

-

-

Определите промежутки монотонности (возрастания, _____________ ) и экстремумы (максимумы и ________________ ) функции.

а

b

max

min

+

7. Найдите значения функции в _________________________ и критических точках.

1. Найдите вторую производную и исследуйте функцию на выпуклость и ____________.

-

с

вогнута

выпукла

+

9. Для построения графика найдите необходимые дополнительные точки.

2.2.3 Дорисуйте схемы

а

-

min

?

?

А) Б)

а

+

?

?

?

К работе допускается ______________

1. Результаты работы

3.1

y =

Изм.

Лист

№ докум.

Подпись

Дата

Лист

ПР. .00.00

1) Область определения функции D(f) =

2) Четность, нечетность функции

f(-x) =

_____________________

3) Точки пересечения графика функции с осями координат

А) с осью ОХ ( у=0)

Б) с осью ОУ ( х=0)

4) Первая производная: y’ =

5) Стационарные точки: (y’ = 0)

____________________

6) Промежутки монотонности (возрастания, убывания)

Возрастает _______________________

Убывает __________________________

7) Экстремумы:

Максимум: x_max = y_max =

Минимум: x_min = y_min =

Изм.

Лист

№ докум.

Подпись

Дата

Лист

ПР. .00.00

8) Вторая производная у ‘’ =

Выпукла ____________________

Вогнута _____________________

9 ) График функции:

х
у

3.2

y =

Изм.

Лист

№ докум.

Подпись

Дата

Лист

ПР. .00.00

1) Область определения функции D(f) =

2) Четность, нечетность функции

f(-x) =

_____________________

3) Точки пересечения графика функции с осями координат

А) с осью ОХ ( у=0)

Б) с осью ОУ ( х=0)

4) Первая производная: y’ =

5) Стационарные точки: (y’ = 0)

____________________

6) Промежутки монотонности (возрастания, убывания)

Возрастает _______________________

Убывает __________________________

7) Экстремумы:

Максимум: x_max = y_max =

Минимум: x_min = y_min =

8) Вторая производная у ‘’ =

Выпукла ____________________

Вогнута _____________________

9 ) График функции:

х
у

Изм.

Лист

№ докум.

Подпись

Дата

Лист

ПР. .00.00

Изм.

Лист

№ докум.

Подпись

Дата

Лист

ПР. .00.00

ПРАКТИЧЕСКАЯ РАБОТА 15

Применение производной для решения задач.

Цель работы

1. 1 Научиться применять производную для решения геометрических и физических задач

1.2 Научиться применять производную для приближённых вычислений

Ход работы

Вариант

2.1.1 Вычислить приближённо е

2.1.2. Найдите тангенс угла наклона к оси ОХ касательной графика функции

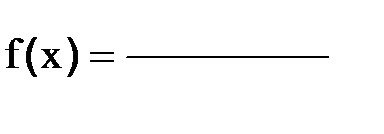
2.1.3 Написать уравнение касательной к графику функции f(x)=

в точке с абсциссой х₀ =

2.1.4 Материальная точка движется прямолинейно по закону

x(t) =

а) Записать формулы для вычисления скорости и ускорения движения

б) Найти скорость и ускорение в момент времени t =

в) Через сколько секунд после начала движения точка остановиться?

2.1.5 Найдите наибольшее и наименьшее значение функции f(x)=

на отрезке [ ; ]

2.1.6 Решите задачу:

________________________________

Изм.

Лист

№ докум.

Подпись

Дата

Лист

ПР. .00.00

2.2. Допуск к работе

2.2.1. В чём заключается физический смысл производной

________________________________

2.2.2. Каков геометрический смысл производной?

________________________________

Изм.

Лист

№ докум.

Подпись

Дата

Лист

ПР. .00.00

2.2.3. Запишите уравнение касательной к графику функции

________________

2.2.4. Запишите алгоритм нахождения наибольшего и наименьшего значения функции на отрезке

________

________

________

________________________

________________

2.2.5. Запишите формулу для вычисления приближённого значения функции

________________

________

К работе допускается ______________

Результаты работы

Изм.

Лист

№ докум.

Подпись

Дата

Лист

ПР. .00.00

ПРАКТИЧЕСКАЯ РАБОТА 16