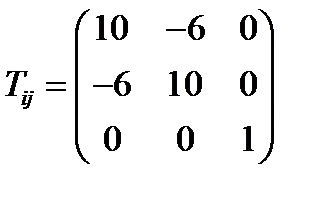Симметричного тензора 2-го ранга

При определении тензора 2-го ранга в параграфе 9 мы исходили из того, что каждому направлению 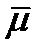в пространстве с помощью тензора 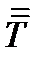ставится в соответствие вектор 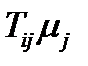. Проекция этого вектора на то же направление:

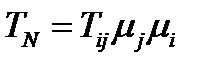(217)

называется нормальной составляющей тензора 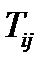в направлении 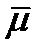. Если единичный вектор 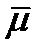совпадает с ортом какой-либо координатной оси, например, 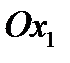, то компоненты вектора 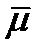будут равны: 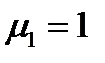, , 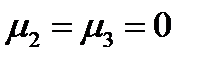и тогда нормальная составляющая (217) окажется просто диагональной компонентой тензора 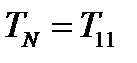. Аналогично две другие диагональные компоненты тензора 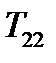и 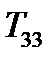являются нормальными составляющими в направлении координатных осе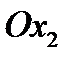й и .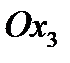

В системе координат, построенной на главных осях тензора, формула для вычисления его нормальной составляющей принимает простой вид. Считая, что 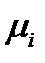– компоненты единичного вектора 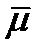относительно главных осей тензора, получим:

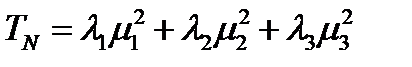(218)

Если, в частности, два главных значения тензора совпадают 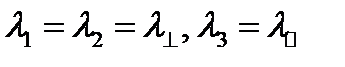, то его нормальная составляющая зависит только от компоненты :

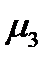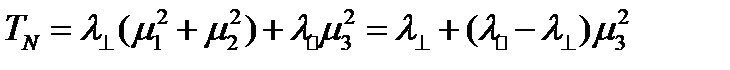(219)

Наконец, при совпадении всех трех главных значений тензора 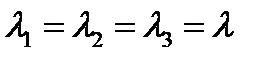нормальная составляющая .

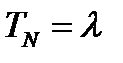Нормальные составляющие часто встречаются в кристаллофизике, и поэтому важное практическое значение приобретает вопрос, в каком направлении нормальная составляющая данного тензора принимает экстремальное значения. Математическая формулировка этой задачи такова: найти значения 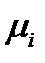, при которых функция (217) достигает экстремума при дополнительном условии 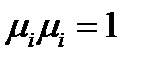. Это типичная задача на условный экстремум и решается она методом неопределенных множителей Лагранжа. Составляется функция Лагранжа:

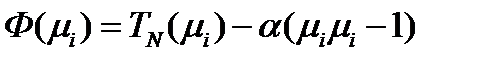(220)

с неопределенным пока множителем 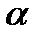и ищется ее безусловный экстремум, т.е. приравниваются к нулю ее частные производные: 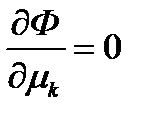, 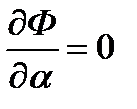. Чтобы найти производные, подставим в (220) выражение (217) и после небольших преобразований получим: 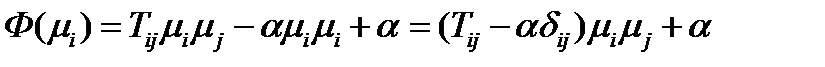(221)

Теперь дифференцируем:

.

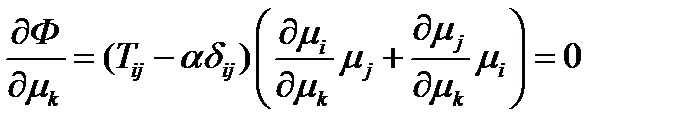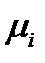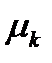Производная от компоненты по равна 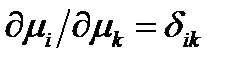. Аналогично, 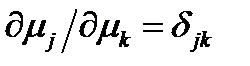. Тогда:

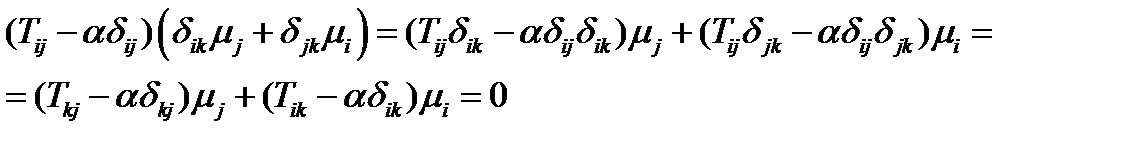Переобозначив в первом слагаемом немой индекс 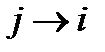, и используя симметрию тензора, получим окончательно: 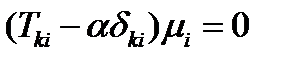, или

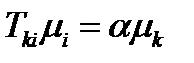(222)

Но это не что иное, как уравнение (158), определяющее главные направления тензора, а 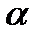, следовательно, главное значение. Таким образом, нормальная составляющая тензора достигает экстремальных значений на главных направлениях этого тензора. Чтобы найти, чему равняются экстремальные значения нормальной составляющей, умножим (222) на :

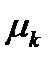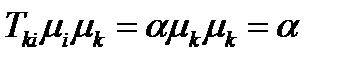, (223)

т.е. экстремальные значения нормальной составляющей равны соответствующим главным значениям тензора.

Из доказанного следует, что если все главные значения тензора положительны (отрицательны), то и все его нормальные составляющие обладают этим свойством. Если же среди главных значений тензора имеются и положительные и отрицательные, нормальная составляющая тензора также принимает и положительные, и отрицательные значения. Будучи непрерывной функцией направления, она при этом на некотором направлении должна обращаться в нуль.

Перейдем к рассмотрению тангенциальных (касательных) составляющих симметричного тензора 2-го ранга. Пусть 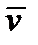и 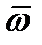– взаимно перпендикулярные единичные векторы, т.е.

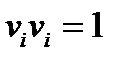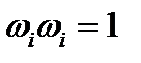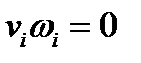, , (224)

Определение. Тангенциальной составляющей тензора 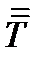в направлениях 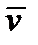и 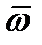называется число:

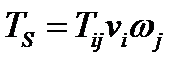(225)

Так как тензор 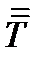симметричен, направления 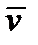и 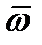в этом определении равноправны и взаимозаменяемы.

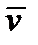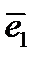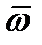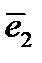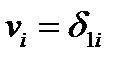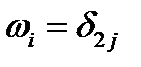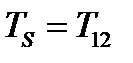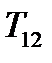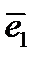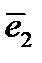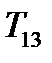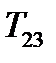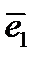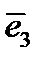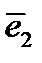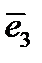
Если, например, вектор совпадает с базисным вектором , а вектор – с базисным вектором , то ; . Подставив в (225), получим: , т.е. компонента тензора является его тангенциальной составляющей в направлениях и . Аналогично получаем, что остальные две недиагональные компоненты тензора и также определяют тангенциальные составляющие для пар направлений , и , Таким образом, в то время как нормальные составляющие соответствуют диагональным компонентам тензора, тангенциальные соответствуют недиагональным компонентам.

В системе координат, построенной на главных осях, тангенциальные составляющие выражаются формулой:

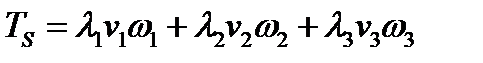(226)

Если два главных значения совпадают 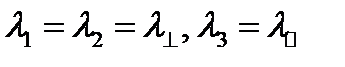, то:

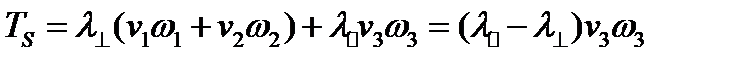(227)

Наконец, при совпадении всех трех главных значений :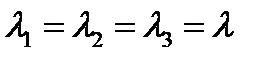

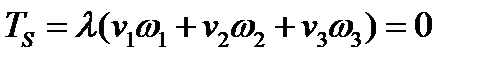(228)

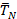Рис. 13

Т.е. все тангенциальные составляющие шарового тензора равны нулю. Отсюда следует, что тангенциальные составляющие произвольного симметричного тензора совпадают с тангенциальными составляющими его девиатора.

Единичные векторы 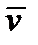и 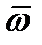в определении (225) однозначно определяют плоскость, ориентация которой в пространстве определяется нормальным вектором 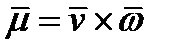(или 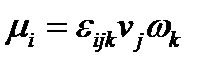). Поэтому вектор 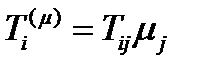, который ставится в соответствие направлению 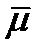, можно разложить на две составляющие: нормальную с величиной 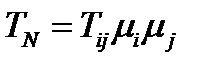, направленную по нормали 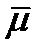к плоскости, и тангенциальную или касательную, направленную вдоль плоскости и имеющую величину: 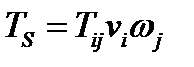(рис.13). Эти две составляющие вектора 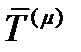связаны теоремой Пифагора, поэтому квадрат тангенциальной составляющей определяется соотношением:

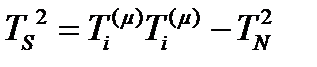(229)

Для тангенциальных составляющих экстремальная задача сложнее, чем для нормальных, но решается тем же методом. Удобнее будет перейти в систему главных осей тензора. Компоненты вектора 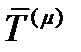будут равны 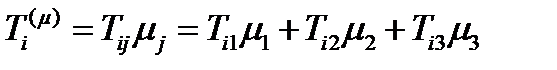, или:

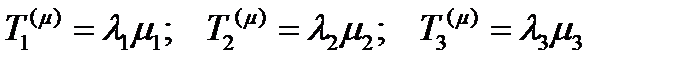(230)

Нормальная составляющая 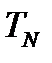в этой же системе координат определяется формулой (218). Подставив (230) и (218) в (229), вычислим квадрат тангенциальной составляющей:

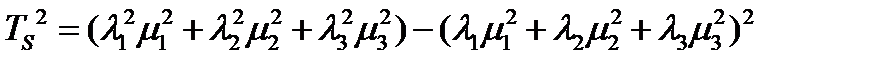(231)

Для исследования на экстремум составляем функцию Лагранжа:

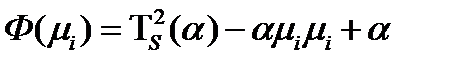(232)

где 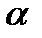– неопределенный пока множитель Лагранжа. Приравнивая к нулю производные функции Лагранжа по 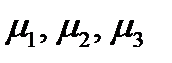и 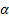, получаем систему уравнений:

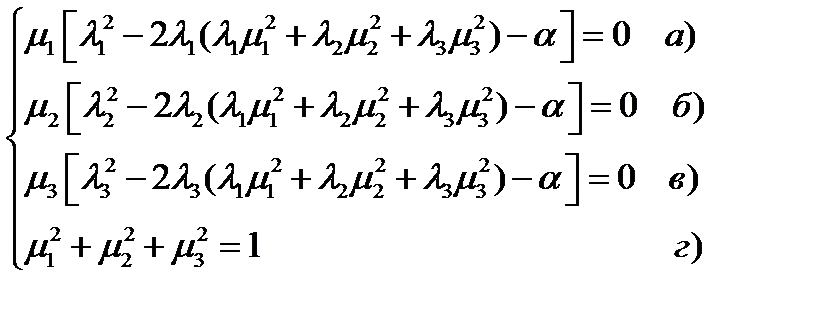(233)

Простейшие решения этой системы и соответствующие им тангенциальные составляющие, вычисляемые по формуле (231), таковы:

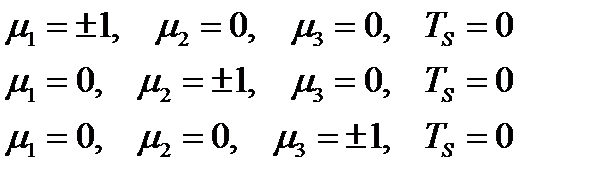(234)

Значение тангенциальной составляющей тензора, определенное этими формулами, очевидно, является минимальным по модулю. Таким образом, как следует из (234), наименьшее значение (по абсолютной величине) тангенциальная составляющая достигает на плоскостях, определяемых главными направлениями тензора. Другие решения системы (233) имеют вид:

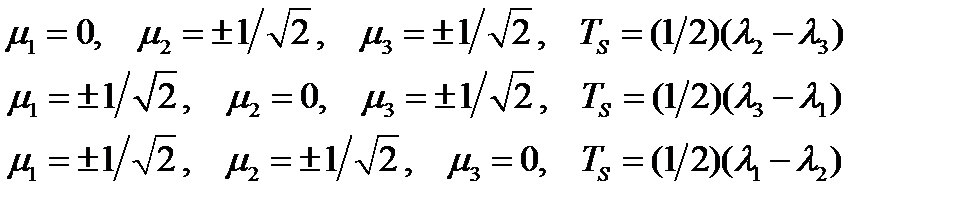(235)

Если главные значения тензора упорядочены по возрастанию, т.е. 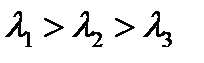, то максимальное по модулю значение тангенциальной составляющей определяется средней формулой и равно полуразности наибольшего и наименьшего главных значений тензора. Оно достигается на плоскости, определяемой биссектрисами углов между главными осями, соответствующими наибольшему и наименьшему главным значениям. Других решений система (233) не имеет. Подробнее решение этой системы будет рассмотрено в задачах.

Задачи.

Задача 27.Вывести характеристическое уравнение (163) из§23.

Решение. В §23 было получено характеристическое уравнение (161) для нахождения главных значений симметричного тензора 2-го ранга. Было сказано, что если раскрыть определитель в (161), то получится кубическое уравнение (163). Проделаем это подробно:

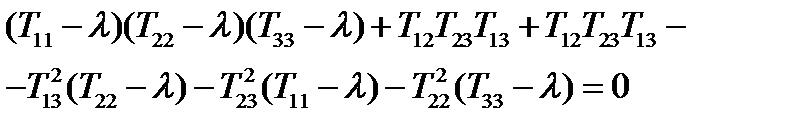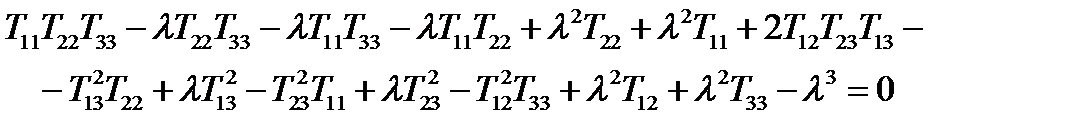, или

, или

.

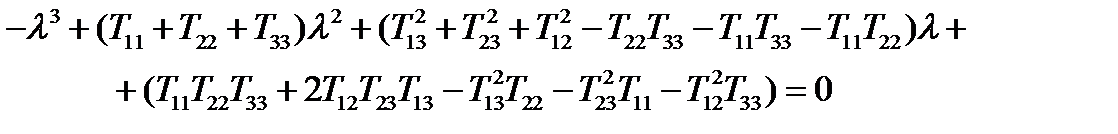Обозначим:

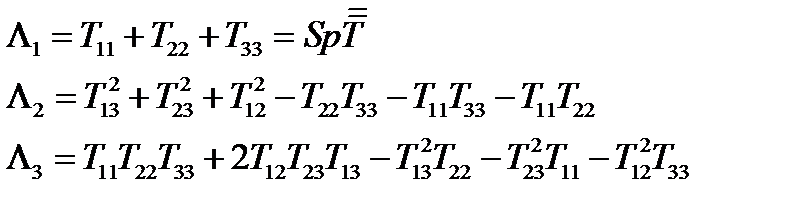(236)

Тогда окончательно 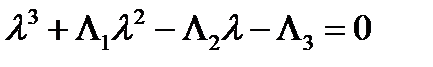, что совпадает с уравнением (163). Если раскрыть определители в (164)-(167), то получим формулы (236). Таким образом, главные инварианты тензора 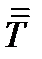определяются формулами (164), (165), (167) или формулами (236).

Задача 28.Доказать ортогональность трех главных направлений в случае трех различных главных значений симметричного тензора 2-го ранга

Решение. В §23 утверждалось, что, если главные значения симметричного тензора 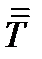различны, то соответствующие им главные направления ортогональны. Доказательство было дано для главных направлени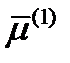й и 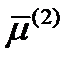. Покажем здесь, что все три главных направления 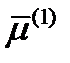, , 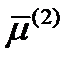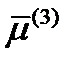ортогональны между собой. Достаточно будет доказать, скажем, ортогональность главных направлени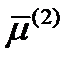й и 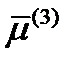. Они удовлетворяют уравнениям:

, .

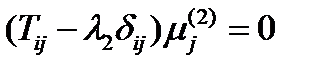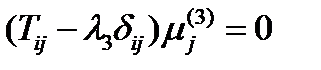Умножим первое из них на 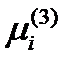, второе – на 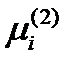, и вычтем их друг из друга: 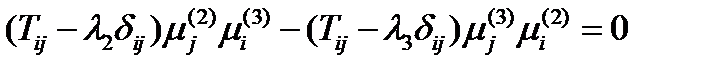, или раскрывая скобки и группируя:

.

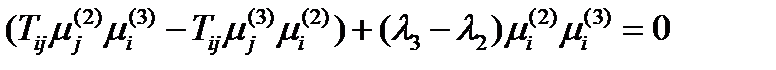Все индексы в этом выражении немые, поэтому их можно переобозначить любыми символами. Во втором слагаемом в первых скобках заменим немые индексы так: 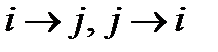. Сделав это, увидим, что выражение в первых скобках обращается в нуль, и тогда 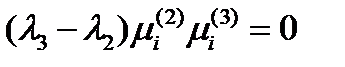. Поскольку 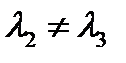, то отсюда следует, что 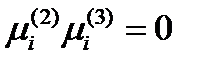, т.е. скалярное произведение единичных главных векторов 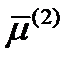и 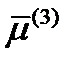равно нулю. Это означает, что 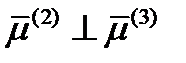. Таким образом, мы получили, что 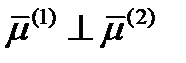, а 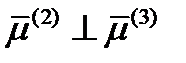. Отсюда следует, что и 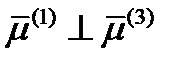. Следовательно, взаимная ортогональность всех трех главных направлений доказана.

Задача 29. Найти главные значения и главные направления тензора 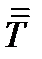: 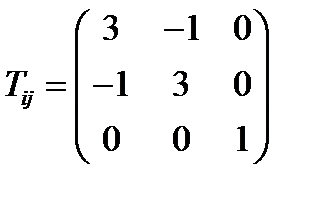(237)

Решение: Главные значения определяются из характеристического уравнения (161), которое в данном случае имеет вид: 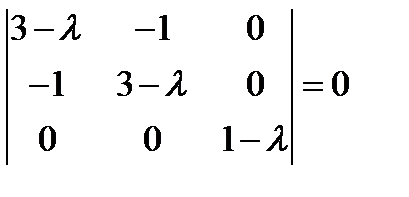. Раскрывая определитель, получаем уравнение 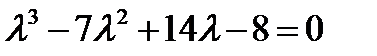. Это кубическое уравнение. Одно его решение находится подбором: 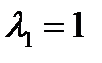. Чтобы найти остальные решения, разделим кубический многочлен на 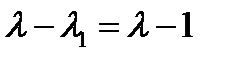. В результате получим квадратное уравнение, корни которого 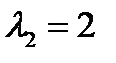, 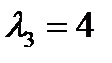. Чтобы найти главное направление, соответствующее 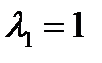, подставим его в систему уравнений (160) и получим: .

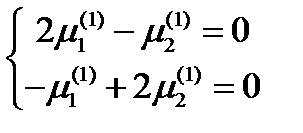Выразим из первого уравнения 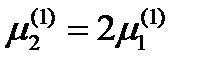и подставим во второе уравнение. Получаем 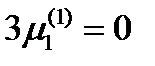. Отсюда 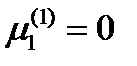, 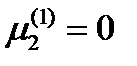. Чтобы найти третью компоненту 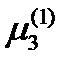, воспользуемся тем, что вектор 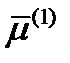единичный и поэтому 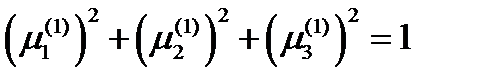. Тогда получим 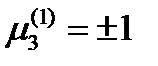. Таким образом, первое главное направление определяется вектором .

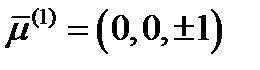Для нахождения второго главного направления, подставим 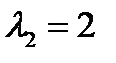в (160): .

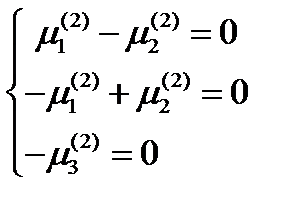Имеем 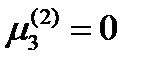, 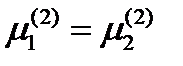. Из условия единичности вектора 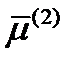получим 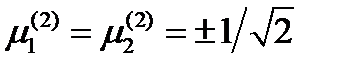. Вектор второго главного направления: .

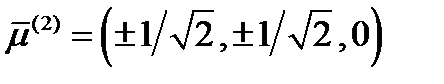Наконец, для третьего главного направления получается система: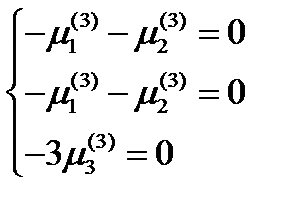

Ее решение 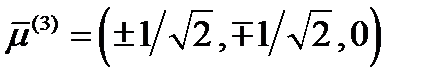. Теперь можно записать матрицу перехода от исходной системы координат, в которой задан тензор (237), к главной, определяемой главными направлениями:

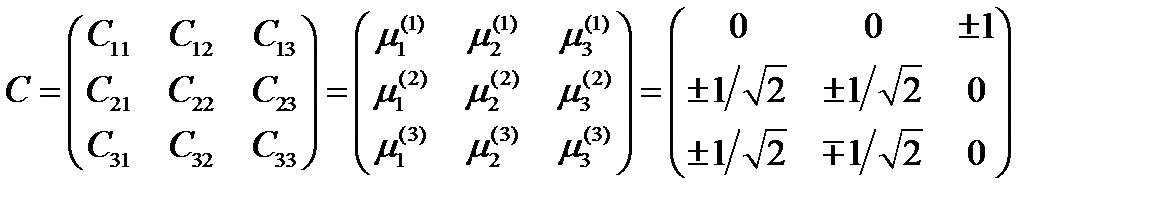(238)

Каждый из полученных векторов 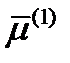, , 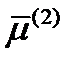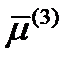определяет два взаимно противоположных направления. Поэтому существуют две главные системы координат в зависимости от того, взят у элементов матрицы (238) верхний или нижний знак. Легко подсчитать, что если взять верхний знак в (238), то 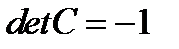; в противоположном случае 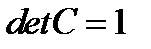. Таким образом, одна из главных координатных систем является левой, а вторая правой. Если ограничиться только правыми системами и считать, что исходная система координат, в которой был задан тензор (237), является правой, то в матрице (238) следует выбрать нижние знаки. После перехода в главную систему координат тензор будет иметь вид: .

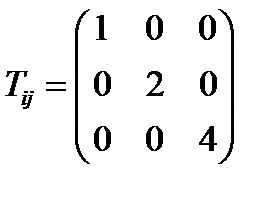Задача 30. Привести к главным осям тензор:

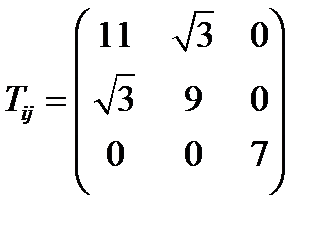(239)

Решение: Характеристическое уравнение имеет вид: 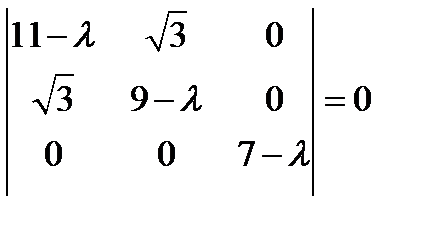, или .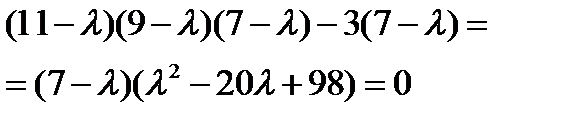

Отсюда: ; ; .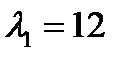

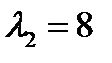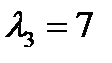Для нахождения первого главного направления, соответствующего главному значению 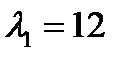, имеем систему:

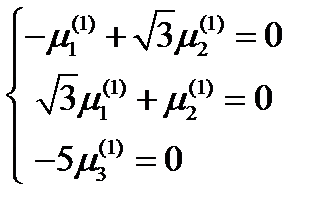
Здесь только два независимых уравнения, так как второе уравнение равно первому, умноженному на 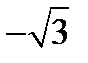. Поэтому находим: 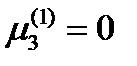, 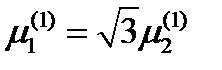. Из условия единичности вектора 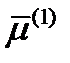находим 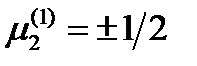, , 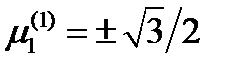т.е. 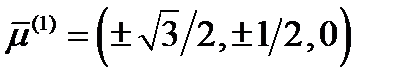. Для второго главного направления, соответствующего 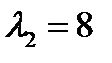, получаем: .

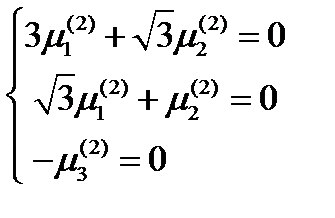Решение системы: 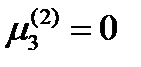, 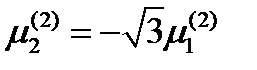. Из условия единичности вектора 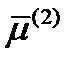окончательно получаем: 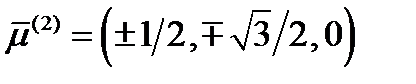. Наконец, для третьего главного направления получаем систему: .

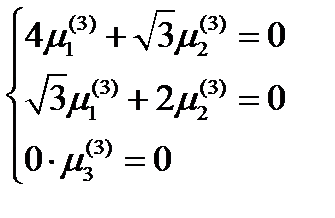Первые два уравнения образуют систему двух однородных линейных уравнений с двумя неизвестными. Определитель ее равен 5. Поэтому она имеет только тривиальное нулевое решение 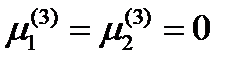. Компонента 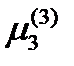может иметь любое значение, но из требования единичности вектора 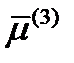следует, что 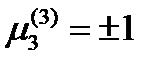. Итак, 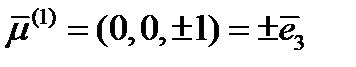, т.е. третье главное направление параллельно

оси 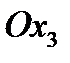. Матрица перехода к главным осям выглядит так: 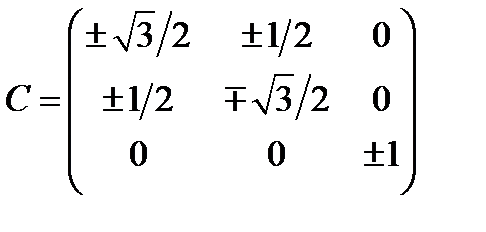(240)

Она определяет две главных системы координат. Чтобы выбрать из них правую, найдем определитель матрицы. Он будет равен +1, если взять нижние индексы у элементов матрицы перехода. Тензор (239) можно теперь записать в соответствии с формулой (175):

.

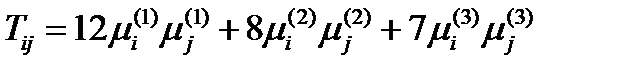Задача 31. Используя построение окружности Мора привести к главным осям тензор

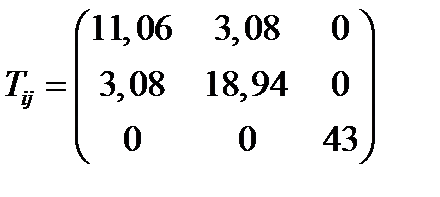(241)

Решение. По формулам (199)-(201), полученным с помощью рис. 12, находим: ; ,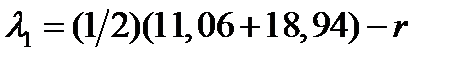

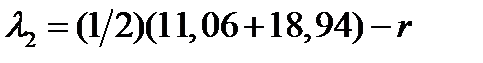где 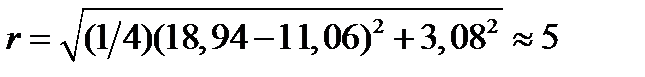, и тогда 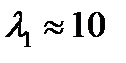, , 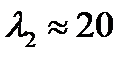, , 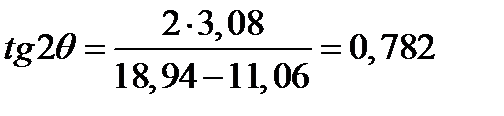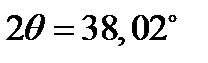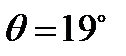. Это означает, что для того чтобы привести тензор (242) к главным осям, нужно повернуть систему координат вокруг оси 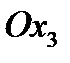на угол 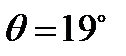в направлении от оси 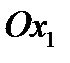к .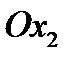

Задача 32. Доказать, что степени симметричного тензора 2-го ранга 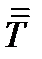также являются симметричными тензорами.

Решение. Квадрат тензора определяется так: 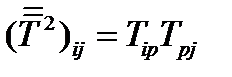. Переставив местами индексы 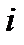и 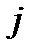, и используя симметричность исходного тензора, получим: 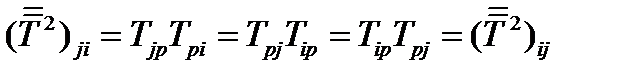. Куб тензора определяется так: 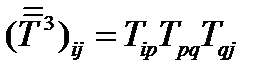. Проделав то же самое, получим: .

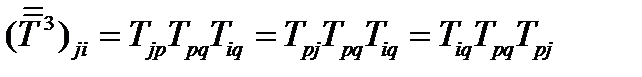Индексы 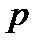и 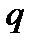немые. Переобозначив их 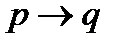, , 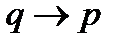и используя симметричность исходного тензора, получаем: 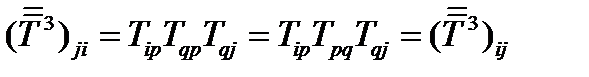. Аналогично доказывается симметричность и любой другой степени тензора .

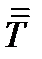Задача 33. Найти главные значения тензора 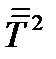и убедиться, что его главные оси совпадают с главными осями тензора 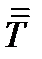из задачи 29.

Решение. Исходный тензор определен в (237). Его квадрат:

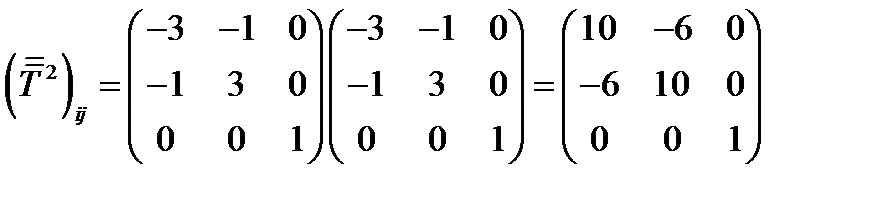(242)

Характеристическое уравнение для тензора 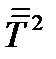имеет вид:

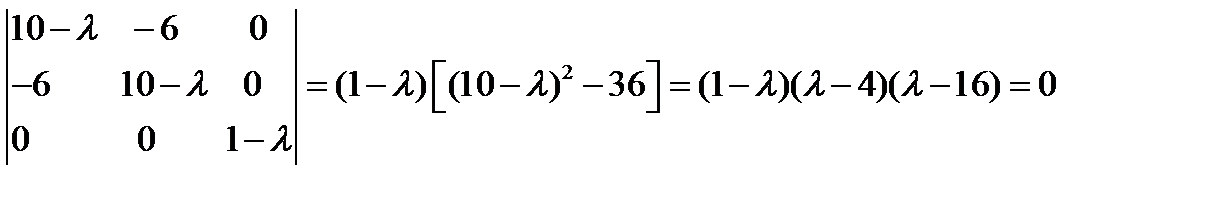(243)

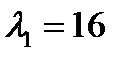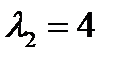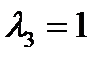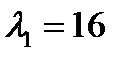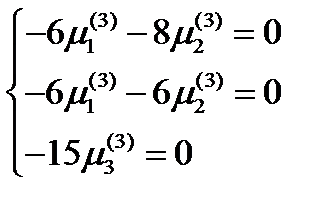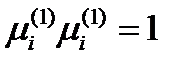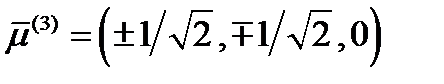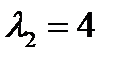Его корни : ; ; . Главное направление для определяется из системы: . Решением этой системы при условии будет вектор . Для имеем систему: 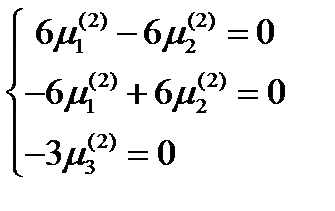. Ее решение: 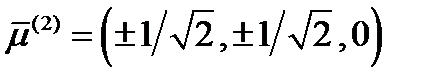. Наконец, для 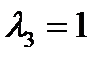имеем систему: 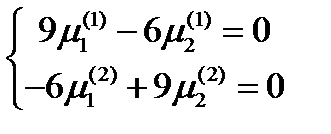. Ее решение: 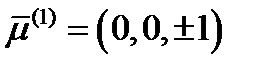. Видно, что главные направления 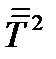и 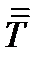одни и те же.

Задача 34. Воспользовавшись тем, что тензор 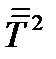и симметричный тензор 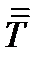имеют одни и те же главные значения, найти тензор 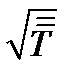, если: 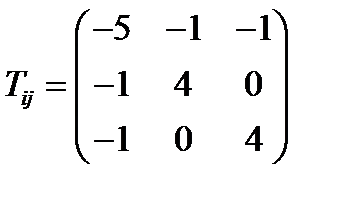(244)

Решение: Прежде всего, будем искать главные значения и главные направления тензора 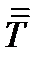. Действуя так же, как в задаче 29, найдем, что в главных осях тензор имеет диагональный вид:

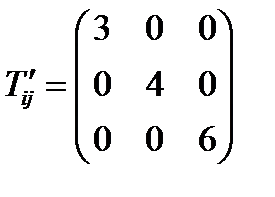, (245)

причем матрица преобразования имеет вид:

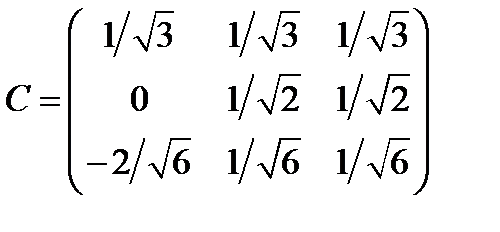(246)

Ясно, что в системе главных осей тензор 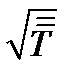должен быть равен:

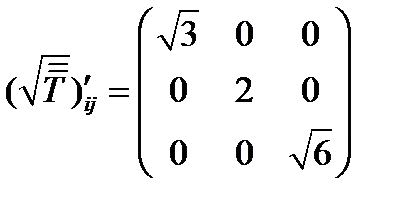(247)

Правильность этого определения подтверждается тем, что, если возвести (247) в квадрат, воспользовавшись формулой (185), то получим (245). Чтобы найти тензор 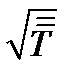в первоначальной системе координат, воспользуемся законом преобразования компонент тензора второго ранга: 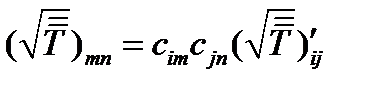. Эту формулу удобнее записать в матричном виде, если под 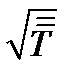и 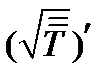понимать матрицы второго порядка. Тогда, вспоминая из курса линейной алгебры операцию умножения матриц, можем записать:

,
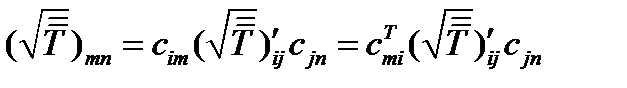или 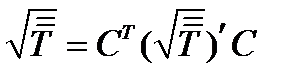(248)

Входящие в правую часть матрицы определены формулами (246), (247), поэтому:

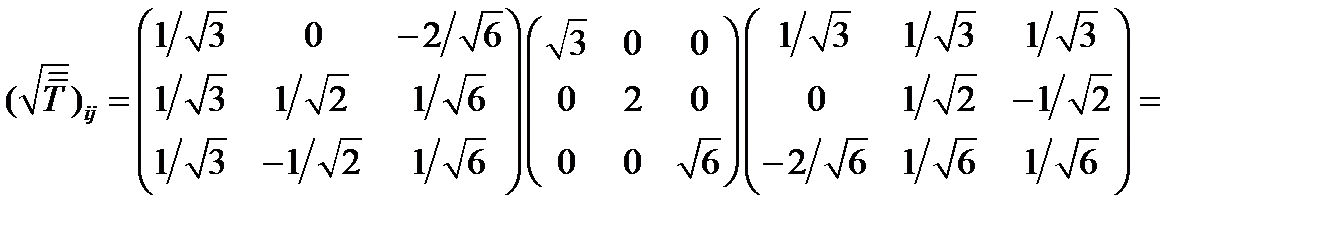
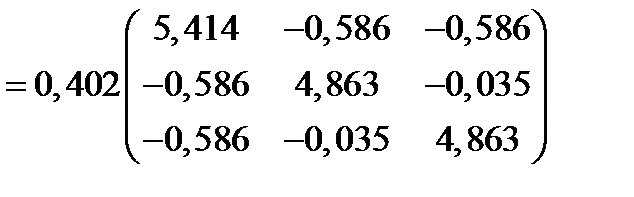(249)

Задача 35. В §27 было доказано, что диагональные компоненты тензора являются его нормальными составляющими в направлениях координатных осей. Доказательство было проведено для компоненты 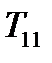. Доказать это утверждение для двух других диагональных компонент.

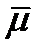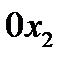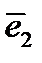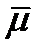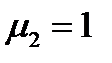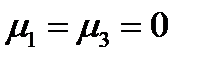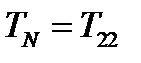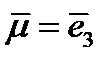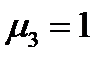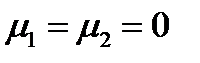Решение: Пусть единичный вектор совпадает с ортом координатной оси , т.е. с базисным вектором . Компоненты вектора при этом равны: , . Подставляя их в формулу (227) и выполняя суммирование, получим: . Аналогично, если вектор , то , и .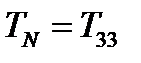

Задача 36. Доказать формулы (226)-(228).

Решение: Тангенциальная составляющая 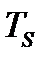симметричного тензора 2-го ранга в направлениях 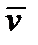и 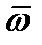, т.е. в плоскости, определяемой этими векторами, была определена формулой (225). Если все главные значения тензора различны, то в системе главных осей он имеет вид (177). Подставляя в (225) и выполнив предусмотренное там суммирование, как раз и получим (226). Если два главных значения тензора совпадают, то он имеет вид (177), и тогда из (225) получим: 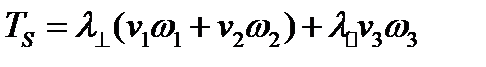(250)

Единичные векторы 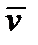и 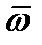по определению ортогональны, т.е. их скалярное произведение 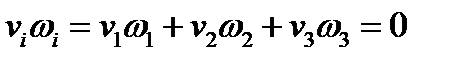. Отсюда 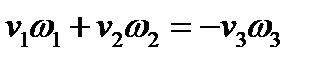и подставив в (250), получим (227). Если же все три главных значения тензора одинаковы, то для 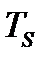получим выражение (228). В силу ортогональности направлени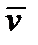й и 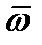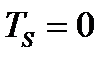, т.е. все тангенциальные составляющие шарового тензора равны нулю.

Задача 37. Решить систему (233).

Решение. Первые два уравнения системы будут удовлетворены, если 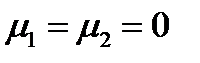. Третья компонента 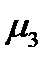не может быть равна нулю, т.к. это противоречит последнему уравнению. Вместо этого из уравнения (233г) получаем, что 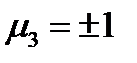. Таким образом, первое решение будет такое: 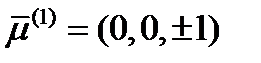. Аналогично получим еще два решения: 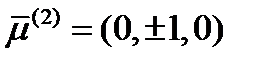и .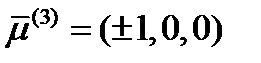

Пусть теперь только одна из компонент вектора 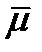равна нулю, а две другие нет. Например, 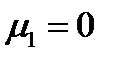. Уравнения (233б,в) могут быть удовлетворены тогда только за счет обращения в нуль выражений в квадратных скобках. Получим: .

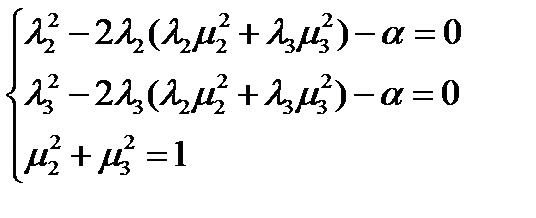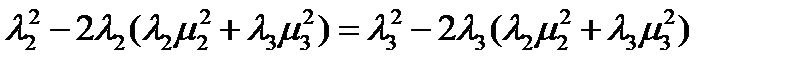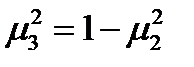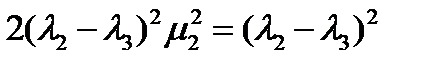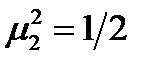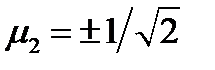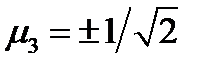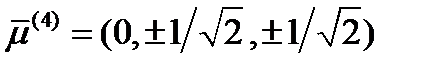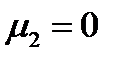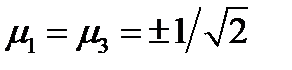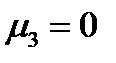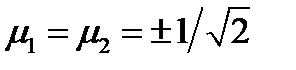Приравняем левые части первых двух уравнений: . Подставив сюда из третьего уравнения , после преобразований получим: . Отсюда: и . Тогда и решение будет такое: . Если , то аналогично получаем . Если же , то . Таким образом, еще два решения будут таким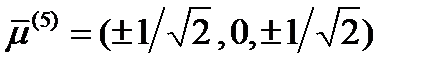и: и .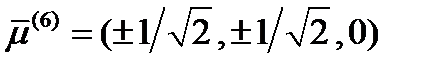

Осталось выяснить, имеет ли система (233) решения, когда все три компоненты 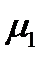, , 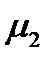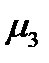отличны от нуля. В этом случае система

принимает вид: .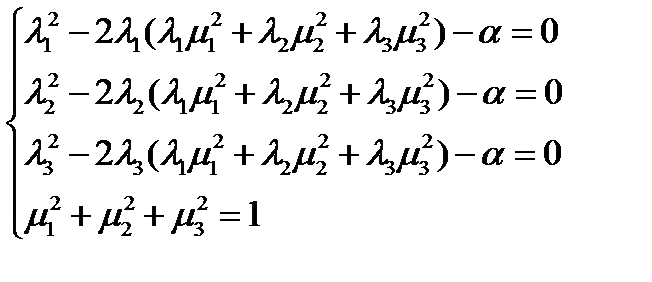

Эту систему можно рассматривать как линейную относительно ,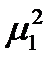

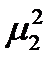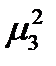, и : .

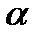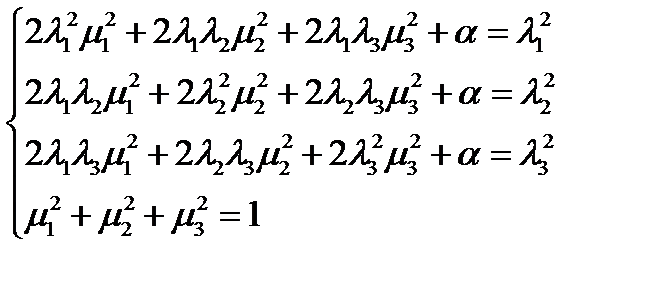Определитель этой системы равен нулю: 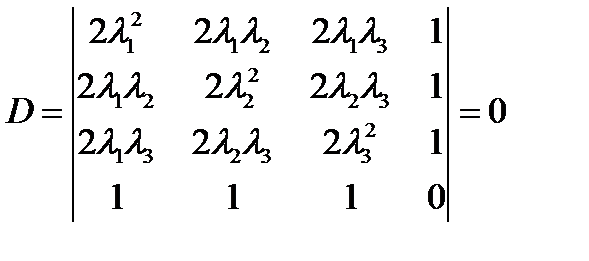. В силу этого система не совместна. Таким образом, других решений, кроме тех, что уже были найдены, система (233) не имеет.

Задача 38. Сколько действительных главных значений имеет антисимметричный тензор 2-го ранга?

Решение. У антисимметричного тензора 2-го ранга диагональные компоненты равны нулю, а недиагональные отличаются знаком. Поэтому характеристическое уравнение антисимметричного тензора имеет вид:

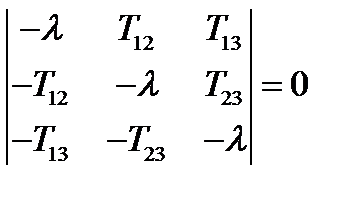, (251)

или в развернутом виде:

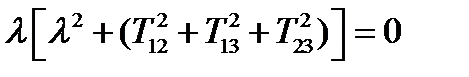(252)

Отсюда видно, что одно главное значение равно нулю, а два других будут комплексными (точнее чисто мнимыми). Вследствие этого и соответствующие им главные векторы тоже будут комплексными. Таким образом, антисимметричный тензор имеет только одно действительное главное значение, равное нулю, и одно действительное главное направление.

Задача 39. Разложить тензор: 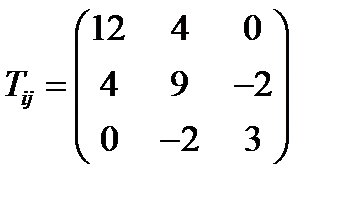на шаровую часть и девиатор, и показать, что первый инвариант девиатора равен нулю.

Решение: Разложение тензора на шаровую часть и девиатор определяется формулой (205) из §26. Имеем:

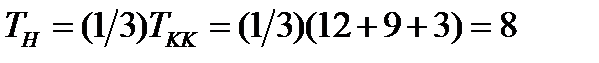. Тогда девиатор будет равен: 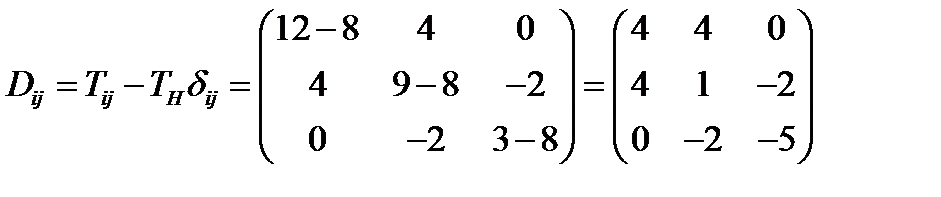. Разложение тензора 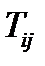будет теперь выглядеть так:

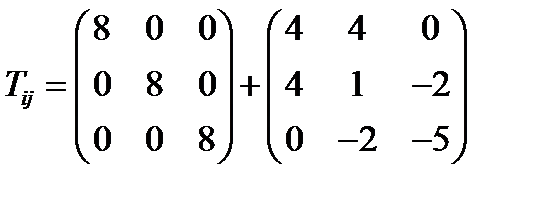. Первый инвариант девиатора – это его след: 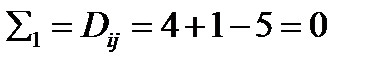, ч.т.д.

Задача 40. Определить главные значения девиатора для тензора