Решение транспортной задачи методом северо – западного угла

Для иллюстрации решения задач методом северо – западного угла рассмотрим на конкретном примере все этапы её решения.

Этап № 1: Начертим матрицу (таблица 13.2) и внесём в ячейки исходные данные задачи: Поставщики: П1(250т), П2(400т), П3(150т), П4(300т). Потребители: К1(500т), К2(100т), К3(300т), К4(200т).

Таблица 13.2.

КJ ПI
	Х11	Х12
	Х21

Нам необходимо вписать в незаполненные ячейки оптимальное количество груза от поставщиков к потребителям, чтобы общая стоимость всех перевозок была минимальной.

Обозначим незаполненные ячейки номерами строк и столбцов:

Х11; Х12; Х13; Х14; …Х21; Х22 и т.д.

Составим математическую модель:

Х11 + Х12 + Х13 + Х14 = 250

Х21 + Х22 + Х23 + Х24 = 400

Х31 + Х32 + Х33 + Х34 = 150

Х41 + Х42 + Х43 + Х44 = 300

Х11 + Х21 + Х31 + Х41 = 500

Х12 + Х22 + Х32 + Х42 = 100

Х13 + Х23 + Х33 + Х43 = 300

Х14 + Х24 + Х34 + Х44 = 200

Х_IJ > 0, i = 1,2,3,4; j = 1,2,3,4.

Нужно найти минимальное значение целевой функции, которая даст оптимальное значение стоимости всех перевозок. Она определяется как сумма произведений объёма перевозок на стоимость перевозки от каждого поставщика к каждому потребителю.

В табл. 13.3. приведены стоимости перевозок 1-ой тонны груза в условных денежных единицах от каждого поставщика к каждому потребителю:

Таблица 13.3.

Запишем целевую функцию:

F = 1 * Х11 + 5 * Х12 + 7 * Х13 + 4 * Х14 + 2 * Х21 + 6 * Х22 + … + 3 * Х44. (13.1)

Этап №2: Составим методом северо – западного угла первое распределение поставок, начиная с заполнения верхней левой («северо – западной») клетки таблицы. Примем объём перевозки от П1 к К1 максимально возможным исходя из условий задачи и равным 250т. Поставщик отдал всю продукцию и строку №1 можно исключить из дальнейшего рассмотрения.

Далее в таблице найдём новый «северо – западный» угол. Это ячейка 21. Помещаем в неё объём перевозки от П2 к К1 равный 250т. Потребитель №1 получил всю продукцию и поэтому весь столбец №1 исключаем из дальнейшего рассмотрения.

Следующим «северо–западным» углом будет ячейка 22. И т. д. Итак, табл. 13.4. является исходным распределением поставок.

Таблица 13.4.

Получим следующее значение целевой функции:

F = 1 * 250 + 2 * 250 + 6 * 100 + 8 * 50 + 3 * 150 + 1 * 100 + 3 * 200 = 2900 (у.е.)

Этап № 3. Для проверки результата на оптимальность необходимо сформулировать математическую модель двойственной исходной с введением 8-ми переменных, значения которых равно 0. Строится таблица из 8-ми строк и 8-ми столбцов, строятся системы неравенств. Если неравенства выполняются, то решение является оптимальным. Если нет, то вводится так называемая «нулевая клетка» и опять строится таблица, в ней строится контур, по которому перемещаются величины поставок в другие клетки. Снова находим целевую функцию. Так, иногда, приходится поступать много раз, пока решение даст оптимальный результат.

Решение транспортной задачи с помощью ЭВМ

Помещаем таблицу 13.4 в стандартную программу EXСEL.

В одной из свободных ячеек за пределами матрицы вычисляем целевую функцию, а именно:

- вводим формулу расчёта суммы произведений стоимости перевозки каждой ячейки на партию поставки;

- находим значение.

В меню открываем «Сервис» и выбираем вкладку «Поиск решения…». Открывается окно, в котором необходимо:

- установить целевую функцию (полученный результат) и установить её равной минимальному значению,

- указать изменяемые ячейки,

- добавить ограничения (приравнять цифры вверху и внизу каждого столбца и каждой строки),

- войти в параметры и выставить число секунд расчёта (рекомендовано выставить 10000), число итераций (количество циклов, расчётов – рекомендовано выставить 10000), величину относительной погрешности (рекомендовано выставить 0,000001), неотрицательность значений, допустимое отклонение (рекомендовано выставить 5%), сходимость (рекомендовано выставить 0,0001),

- нажать клавишу «Выполнить».

Ниже приведена матрица оптимального решения нашей транспортной задачи.

Как видим, при таком распределении стоимость перевозок сократилась почти в два раза.

	234,8214			165,1786
	15,1786			34,8214

F = 1550

В табл. 13.5. приведен окончательный вариант распределения поставок между поставщиками и потребителями

Таблица 13.5 – Оптимальное распределение груза между поставщиками и потребителями

КJ ПI	К1 = 500	К2 = 100	К3 = 300	К4 = 200
П1 = 250
П2 = 400
П3 = 150
П4 = 300

Оптимальный размер целевой функции (стоимость перевозки грузов) равен 1550 у.е.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. Губенко В. К. Общий курс промышленного транспорта : eчебник для вузов / В. К. Губенко, В. Э. Парунакян. – М. : Транспорт, 1994. – 199 c.

2. Губенко В. К. Рециклинг-функция логистической системы / В. К. Губенко, В. М. Бубнов, К. В. Губенко // Вестник Приазовского государственного технического университета. – 1996. – № 2. – С. 207–210.

3. Концептуальная модель логистической системы морского порта / В. К. Губенко, М. М. Дергаусов, Йожеф Челени, М. Ю. Чулочников // Вестник ПГТУ. - Мариуполь, 1995. – № 1. – С. 225 – 229.

4. Губенко В. К. Логистика : учебное пособие / В. К. Губенко. – Мариуполь, 1996. – 265 с.

5. Гаджинский А. М. Основы логистики / А. М. Гаджинский. – М. : Информационно-внедренческий центр «Маркетинг», 1996. – 209 с.

6. Семененко А. И. Предпринимательская логистика / А. И. Семененко. – СПб. : Политехника, 1997. – 156 с.

7. Смехов А. А. Введение в логистику / А. А. Смехов. - М. : Транспорт, 1993. – 112 с.

8. Смехов А. А. Математические модели процессов грузовой работы / А. А. Смехов. – М. : Транспорт, 1982.– 256 с.

9. Рынок и логистика / под ред. М. П. Гордона. – М. : Экономика, 1993. – 143 с.

10. Логистика : учебное пособие / под ред. Б. А. Аникина. – М. : ИНФРА-М, 1999. – 327 с.

11. Доналд Уотерс. Логистика. Управление цепью поставок : перю с англ. – М. : ЮНИТИ-ДАНА, 2003. – 503 с.

12. Сергеев В. И. Логистика в бизнесе : учебник / В. И. Сергеев. – М. : ИНФРА-М, 2001. – 608 с.

13. Логистика : учебное пособие / Аникин Б. А. [и др.]. – М. : ТК Вепби, Изд-во Проспект, 2005. – 408 с.

14. Гаджинский А. М. Практикум по логистике / А. М. Гаджинский. – 2-е изд., перераб. и доп. – М. : Издательско-книготорговый центр «Маркетинг», 2001. – 180 с.

15. Практикум по логистике : учеб. пособие / под ред. Б. А. Аникина. – 2-е изд., перераб. и доп. – М. : ИНФРА-М, 2001. – 280 с.

16. Николайчук В. Е. Логистика / В. Е. Николайчук. – СПб. : Питер, 2001. – 160 с.

17. Логистика : конспект лекций / В. А. Козловский и др. – СПб. : гос. техн. ун-т, Чебоксарский ин-т экономики и менеджмента. – Санкт-Петербург : «Политехника», 1998. – 176 с.

18. Кристофер М. Логистика и управление цепочками поставок : пер. с англ. / М. Кристофер; под общ. ред. В. С. Лукинского. – СПб. : Питер, 2005. – 316 с.

Приложение

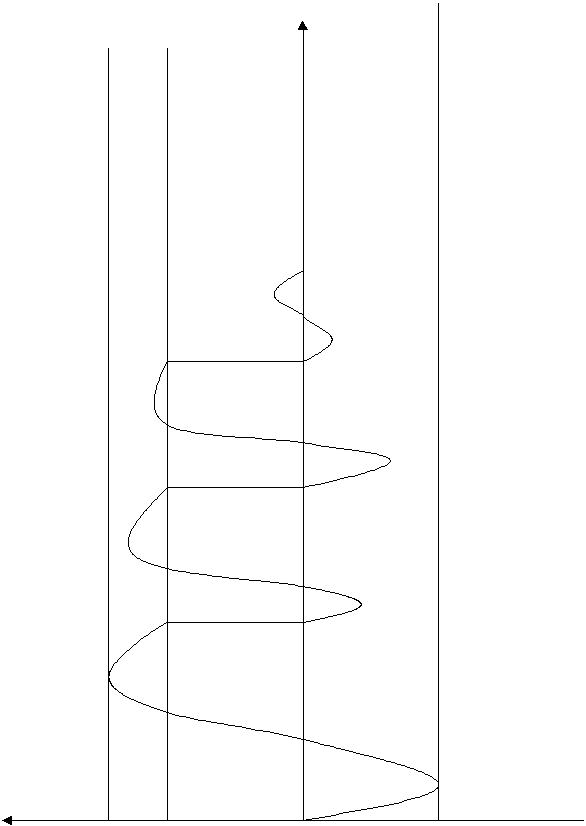
График жизненного цикла существования логистической системы для выполнения лабораторной работы № 3