IV. Работа по теме урока. 1. Ф р о н т а л ь н а я р а б о т а
1. Ф р о н т а л ь н а я р а б о т а.
– Измерьте углы треугольников на рисунке.
– Найдите значение суммы углов каждого треугольника.
а) 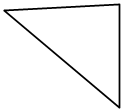 б)
б) 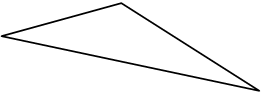
в) 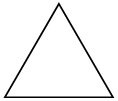 г)
г) 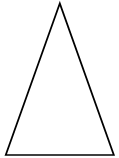
а) 85° + 45° + 50° = 180°
б) 150° + 15° + 15° = 180°
в) 60° + 60° + 60° = 180°
г) 40° + 70° + 70° = 180°
– Какую особенность вы заметили?
– Начертите несколько треугольников в тетради и найдите сумму углов каждого из них.
– Какой вывод вы можете сделать? (Сумма углов треугольника равна 180°.)
– Когда вы будете изучать геометрию, то это утверждение вы научитесь доказывать. А пока мы познакомимся с ним на основе проведенных наблюдений.
Вы уже научились измерять длины отрезков и величин углов, площади некоторых многоугольников. Все эти фигуры называются геометрическими. С геометрическими фигурами имели дело с древних времен и крестьяне, и ремесленники, и строители храмов. дворцов и пирамид. Надо было уметь измерять площади земельных участков, подсчитывать объем корзин, в которые собирали урожай, определять, сколько камня потребуется для здания. А чтобы здание не рушилось, стены надо было возводить под прямым углом к поверхности земли. Астрономам древности необходимо было измерять углы для определения положения небесных светил.
Особенно быстро знания о свойствах фигур развились в Древнем Египте.
В этом государстве все земледелие было сосредоточено на очень узкой полосе земли – в долине реки Нил. Земли было мало, за участок крестьянин ежегодно платил соответствующий налог фараону.
Каждую весну Нил разливался и удобрял землю плодородным илом. Но при разливе смывались границы участков, менялись площади.
Тогда пострадавшие обращались к фараону, а фараон посылал землемеров, чтобы восстановить границы участков, выяснить, как изменилась их площадь, и установить размер налога.
В Древнем Египте развивались и строительное искусство, и торговля. Знания постепенно накапливались, систематизировались. Около 4 тыс. лет назад возникла наука об измерении расстояний, площадей и объемов, о свойствах различных фигур. Так как в основном речь шла о земельных участках, то древние греки, узнавшие об этой науке от египтян, назвали ее геометрией (по-гречески «гео» – земля, а «метрео» – измеряю. Значит, «геометрия» буквально означает «землемерие»). Греческие ученые узнали много новых свойств геометрических фигур, и уже тогда геометрией стали называть науку о геометрических фигурах, а для науки об измерении земли ввели другое название – «геодезия» (происходит от греческих слов «деление земли»).
С п р а в о ч н ы й м а т е р и а л д л я у ч и т е л я
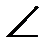 MNK = 50° – градусная мера угла MNK равна пятидесяти градусам или угол MNK равен пятидесяти градусам.
MNK = 50° – градусная мера угла MNK равна пятидесяти градусам или угол MNK равен пятидесяти градусам.
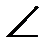 А –
А – 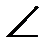 В = 8° – разность градусных мер углов А и В равна восьми градусам.
В = 8° – разность градусных мер углов А и В равна восьми градусам.
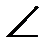 С +
С + 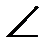 D = 120° – сумма углов С и D равна ста двадцати градусам.
D = 120° – сумма углов С и D равна ста двадцати градусам.
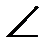 АОВ >
АОВ > 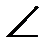 СОD – угол АОВ больше угла СОD или градусная мера угла АОВ больше градусной меры угла СОD.
СОD – угол АОВ больше угла СОD или градусная мера угла АОВ больше градусной меры угла СОD.
Слово «градус» – латинское, означает «шаг», «ступень». Измерение углов в градусах появилось более 3 тыс. лет назад в Вавилоне. В расчетах там использовались шестидесятеричная система счисления, шестидесятеричные дроби.
С этим связано, что вавилонские математики и астрономы, а вслед за ними греческие и индийские, полный оборот (окружность) делили на 360 частей – градусов (шесть раз по шестьдесят), каждый градус – на 60 минут, а минуту – на 60 секунд.
1° = 60', 1' = 60''
В конце XVIII века при разработке метрической системы мер французские ученые предложили делить прямой угол не на 90, а на 100 частей. Такой угол 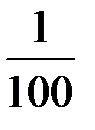 прямого угла называют «град»: 90° = 100 град.
прямого угла называют «град»: 90° = 100 град.
В градах измеряют углы в геодезии, этой единицей пользуются в некоторых строительных расчетах, но широкого распространения она не получила. Для точного измерения углов созданы различные инструменты. Основная часть этих приборов – шкала, похожая на шкалу транспортира.
2. Р а б о т а п о к а р т о ч к а м.
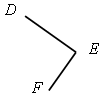
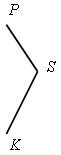
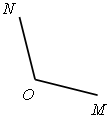
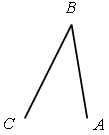
Измерьте иглы, изображенные на рисунке, и запишите результаты измерений.
 Ф и з к у л ь т м и н у т к а
Ф и з к у л ь т м и н у т к а
