Законы распределения вероятностей дискретных СВ

Блок А (12 вопросов,12 баллов, )

1. Определение вероятности

2. Теоремы сложения и умножения

3. Полная вероятность. Формула Байеса

4. Законы распределения вероятностей дискретных СВ

5. Законы распределения вероятностей непрерывных СВ

6. Числовые характеристики ДСВ

7. Статистическое распределение выборки

8. Характеристики вариационного ряда

9. Точечные оценки параметров распределения

10. Интервальные оценки параметров распределения

11. Элементы корреляционного анализа

12. Проверка статистических гипотез

Блок В (6 вопросов по 2 балла. Итого 12 баллов)

13. Основные понятия и теоремы ТВ

14. законы распределения вероятностей СВ

15. Числовые характеристики СВ

16. Основные понятия и задачи МС

17. Статистические оценки параметров распределения

18. Корреляционный анализ и статистические гипотезы

Кейсы -16 баллов

Баллов

20.1 -1 балл

20.2- 3 балла

20.3- 2 балла

Баллов

21.1- 2 балла

21.2- 2 балла

21.3-1 балл

Баллов

22.1-1

22.2-2

22.3-2

Итог- 41 балл

Блок А ( все вопросы по 1 баллу)

Определения вероятности

1/1. Из урны, в которой находятся 6 черных, 4 белых и 10 зеленых шаров, вынимают случайным образом 1 шар. Определить вероятность того, что он белый.

А) 0,25 в) 0,3 с) 0,2 г) 0,4

1/2 Бросаются 2 игральные кости. Определить вероятность того, что на них выпадет разное число очков, сумма которых не превышает 4

1/3 Бросаются 2 игральные кости. Определить вероятность того, что на них выпадет разное число очков, сумма которых не превышает 3

1/4Точка наудачу поставлена на отрезок [-1;13]. Тогда вероятность того, что она попадет и на отрезок [5;9] равна…

1) 5/7 2) 2/7 3) 1/3 4) 2/3

1/5После бури на участке между 50 и 70 км высоковольтной линии передач произошел обрыв проводов. Тогда вероятность того, что авария произошла между 60 и 63 км равна…

1/6В урне находится 6 черных, 4 белых и 10 зеленых шаров. Определить вероятность того, что случайным образом извлеченный шар- белый

9/2. Из урны, в которой находятся 3 черных, 9 белых и 8 зеленых шаров, вынимают случайным образом один шар. Тогда вероятность того, что этот шар не будет белым, равна …

9/3. В круг с радиусом 5 помещен меньший круг с радиусом 3. Тогда вероятность того, что точка, брошенная в больший круг, попадет также и в меньший круг, равна..

9/4. При наборе телефонного номера абонент забыл две последние цифры и набрал их наудачу, помня только, что эти цифры нечетные и разные. Тогда вероятность того, что номер набран правильно, равна…

а) 1/5 б) 1/90 в) 1/4 г) 1/20

Теоремы сложения и умножения

2/1 Из урны, в которой лежат 8 белых и 2 черных шара наудачу, по одному извлекают 2 шара без возвращения. Тогда вероятность того, что первым был извлечен черным, а вторым белый равна..

2/2 В группе из 11 студентов 6 отличников. наудачу отобраны 4 студента. Тогда вероятность того, что среди отобранных студентов нет отличников, равна…

2/3 Наладчик обслуживает 3 станка. Вероятность того, что в течении часа потребует его вмешательство первый станок равна 0,2, второй-0,15, третий -0,1. Тогда вероятность того, что в течение часа не потребует внимания только третий станок, равна..

2/4 Из урны, в которой лежат 7 белых и 13 черных шара наудачу, по одному извлекают 2 шара без возвращения. Тогда вероятность того, что оба шара будут белыми равна..

1) 21/190 2) 39/95 3) 21/200 4) 49/400

2/5Из урны, в которой лежат 6 белых и 4 черных шара наудачу, по одному извлекают 2 шара без возвращения. Тогда вероятность того, что первым был извлечен белый, а вторым черный равна..1) 4/15 2) 3/15 3) 6/25

2/6Студент на сессии сдает 3 экзамена. Для каждого из них вероятность сдачи равна 0,8. Определить вероятность того, что их 3-х экзаменов сдан хотя бы один

Полная вероятность. Формула Байеса

3/1 В первой урне 6 белых и 4 черных шара. Во второй урне 8 белых и 2 черных. Из наудачу взятой урны извлечен шар. Он оказался черным. Определить вероятность того, что этот шар вынули из первой урны.

1) 0,7 2) 1/3 3) 2/3 4) 0,3

3/2 Вероятность изготовления бракованного изделия на первом станке равна 0,15 на втором 0,1. Производительность первого станка втрое больше, чем второго. Наудачу взятая деталь оказалась бракованной. Тогда вероятность того, что она изготовлена на втором станке равна…

3/3 В первой урне 8 белых и 4 черных шара. Во второй урне 3 белых и 5 черных. Из наудачу взятой урны извлечен шар. Тогда вероятность того, что этот шар белый равна….

1) 25/24 2) 1/2 3) 19/48 4) 25/48

3/4 В первой урне 7 белых и 3 черных шара. Во второй урне 1 белый и 9 черных. Из наудачу взятой урны извлечен шар. Он оказался черным. Определить вероятность того, что этот шар вынули из второй урны. 1) 1/4 2) 3/4 3) 3/5

3/5 С первого станка на сборку поступает 80%, а со второго-20%. Среди деталей первого станка бракованных 3%, со второго-4%. Тогда вероятность того, что поступившая на сборку деталь бракована равна..

Законы распределения вероятностей дискретных СВ

4/1.Дискретная случайная величина задана законом распределения вероятностей . Тогда a и b могут быть равны… (а=0,66; b=0,28 а=0,02; b=0,04 а=0,18; b=0,28 а=0,12; b=0,04)

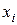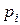	0,08	a	b	0,38	0,48

4/2.Дискретная случайная величина задана законом распределения вероятностей . Тогда вероятность 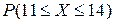равна…

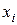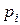	0,25	0,2	0,15	0,4

4/3 Для дискретной случайной величины Х:

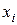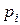	Р1	Р2	Р3	Р4

функция распределения вероятностей имеет вид:

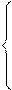0, при х ≤ 9

0,24 при 9 < х ≤ 10

F(x)= р при 10 < х ≤ 12

0,78 при 12 < х ≤ 14

1 при х > 14

Тогда значение параметра р может быть равно….

4/4Вероятность появления некоторого события в каждом из 3000 независимых испытаний постоянна и равна 0,0025. Тогда вероятность того, что событие появиться ровно 6 раз, следует вычислить с использованием Формулы Пуассона

4/5.Дискретная случайная величина задана законом распределения вероятностей . Тогда вероятность 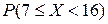равна…

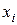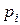	0,45	0,15	0,35	0,05

1) 0,55 2) 0,5 3) 0,85 4) 0,95

4/6.Дискретная случайная величина задана законом распределения вероятностей . Тогда a равно…

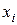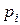	0,15	0,25	0,35	а

4/7ДСВ задана законом распределения вероятностей. Тогда 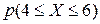равна…

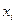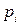	0,2	0,1	0,3	0,4