IV. Работа по теме урока. 1. Ф р о н т а л ь н а я р а б о т а

1. Ф р о н т а л ь н а я р а б о т а.

– Как справедливо разделить пять разных пирожных между четырьмя детьми?

– Выполните схематичный рисунок к решению этой задачи.

– На сколько равных частей нужно разделить каждое пирожное? (Каждое пирожное нужно разделить на 4 части.)

– Сколько таких частей окажется у каждого из друзей? (У каждого окажется 5 таких частей – по одной от каждого пирожного.)

– Как записать количество пирожных у каждого? (Количество пирожных у каждого равно .)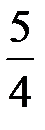

– Можно ли это дробное число записать по-другому?

– Отметьте точку А 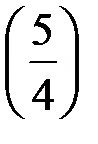на числовом луче.

– Какой единичный отрезок будет использовать? (4 клетки.) Почему?

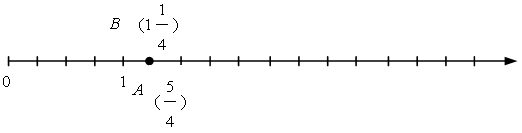
– Отметьте на этом же луче точку В .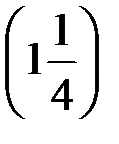

– Точки А и В совпали на координатном луче.

– Как вы думаете, верно ли равенство: 1 = ?

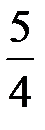С п р а в о ч н ы й м а т е р и а л д л я у ч и т е л я

Ÿ Правильные и неправильные дроби

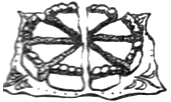
– Разрезали пирог на 8 равных частей (рис. 1, а) и 3 части положили на тарелку.

а

б

в

Рис. 1

На ней оказалось 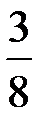пирога (рис. 1, б). Если положить все 8 частей, то на тарелке будет 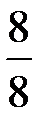пирога, то есть весь пирог (рис. 1, в).

Значит, 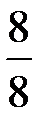= 1.

Возьмем еще один такой же пирог и разрежем его тоже на 8 равных частей (рис. 2, а). Если на тарелку положить, например, 11 частей, то там будет 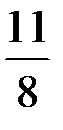пирога (рис. 2, б).

а

б

Рис. 2

В дроби 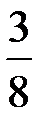числитель меньше знаменателя. Такие дроби называют правильными. В дроби 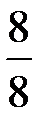числитель равен знаменателю, а в дроби 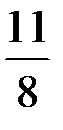числитель больше знаменателя. Такие дроби называют неправильными.

Дробь, в которой числитель меньше знаменателя, называют правильной дробью.

Дробь, в которой числитель больше знаменателя или равен ему, называют неправильной дробью.

Правильная дробь меньше единицы, а неправильная дробь больше или равна единице (рис. 3).

Рис. 3

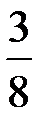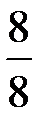< 1, 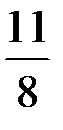= 1, > 1

2. В ы п о л н е н и е задания № 380.

– Прочитайте условие задачи.

– Что известно в задаче? Что требуется узнать?

– Как удобно выполнить краткую запись к данной задаче?

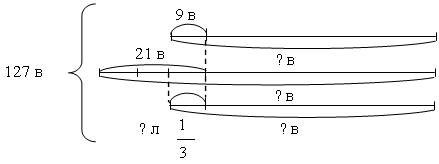
Р е ш е н и е:

1) 21 : 3 = 7 (в.) – съели с третьей тарелки.

2) 9 + 21 + 7 = 37 (в.) – съели всего.

3) 127 – 37 = 90 (в.) – осталось на трех тарелках.

4) 90 : 3 = 30 (в.) – осталось на каждой тарелке.

5) 30 + 9 = 39 (в.) – было на второй тарелке.

6) 30 + 21 = 51 (в.) – было на первой тарелке.

7) 30 + 7 = 37 (в.) – было на третьей тарелке.

О т в е т: 39 в., 51 в., 37 в.

– В чем трудности этой задачи?

П р и м е ч а н и е. Задача для учеников третьего класса представляет значительную трудность, так как ее решение требует выполнения большого числа шагов (7 действий).

– Измените вопрос задачи так, чтобы решение стало короче на 2 действия. (Достаточно, чтобы спрашивалось о количестве вишен на любой одной тарелке.)

– Измените условие новой задачи так, чтобы решение стало еще короче. (Можно, например, указать, что с третьей тарелки съели 7 вишен, решение станет на одно действие короче.)

Ф и з к у л ь т м и н у т к а