Решение уравнения колебаний методом Рунге-Кутта

Цель: сформировать у студентов умение решать системы алгебраические уравнения, используя современные программные средства

(2 часа)

Задание: Найти приближенное решение уравнения колебаний, удовлетворяющее заданным начальным условиям

, .

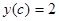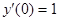В таблице 10 приведены варианты задания.

Таблица 13 Варианты задания

Вариант	Уравнение

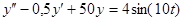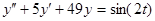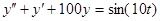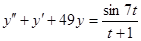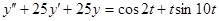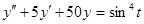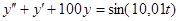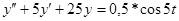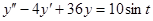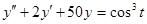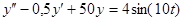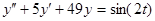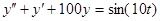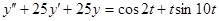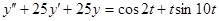Порядок выполнения работы

1. Свести уравнение второго порядка к системе двух уравнений первого порядка.

2. Найти приближённое решение системы двух уравнений методом Рунге-Кутты

3. Проанализировать решение: интервал 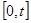, шаг h выбрать самостоятельно так, чтобы по графику можно было определить характер поведения динамической системы (затухающие колебания, нарастающие колебания и т.д.).

4. Построить график приближённого решения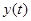

Контрольные вопросы

1. Дайте определение нормальной системы дифференциальных уравнений.

2. Сформулируйте задачу Коши для нормальной системы дифференциальных уравнений.

3. В чем состоит метод Рунге-Кутта для решения уравнения колебаний?

Библиографический список

Основная литература

1. Бахвалов, Н.С. Численные методы / Н.С. Бахвалов. Н. П. Жидков, Г. М. Кобельков. – М.: Бином. Лаборатория знаний, 2008. – 170 с.

2. Вержбицкий, В.М. Основы численных методов. / В.М. Вержбицкий. – М.: Высшая школа, 2002.– 840 с.

3. Макаров, Е.Г. Инженерные расчеты в Mathcad 15: учебный курс. / Е.Г.Макаров. – СПб.: Питер, 2011. – 400 с.

4. Макаров, Е.Г. Mathcad 14:учебный курс. / Е.Г.Макаров. – СПб.: Питер, 2009.– 384 с.

5. Макаров, Е.Г. Инженерные расчеты в Mathcad 14: учебный курс. / Е.Г.Макаров. – СПб.: Питер, 2007. – 592 с.

6. Очков, В.Ф. Mathcad 8 Pro для студентов и инженеров / В.Ф. Очков. – СПб.: БХВ-Петербург, 2008. – 523 с.

7. Поршнев, С.В. Численные методы на базе MathCad. / С.В. Поршнев, И.В. Беленкова. – СПб.: БХВ-Петербург, 2005, - 450 с.

8. Понтрягин, С. Обыкновенные дифференциальные уравнения / С. Понтрягин. – М.: Наука, 1974. – 358 с.

Дополнительная литература

1. Казаков, Ю. В. Математические методы и модели в расчетах на ЭВМ: лабораторный практикум «Дифференциальные уравнения и динамические системы». / Ю. В. Казаков, А. Ю. Казаков. – Красноярск: СибГТУ, 2000. – 36 с.

2. Ушанов, С.В. Решение задач математического программирования в табличном процессоре Excel: уч. пособие /С.В. Ушанов,

В.В. Соболева – Красноярск: СибГТУ, 2002. – 151 с.

Интернет - ресурсы

1. Базовые программы Microsoft Office (Word, Excel),

2. Математический пакет MathCad.

3. Федеральный портал «Российское образование».

Каталог образовательных Интернет-ресурсов - http://www.edu.ru.

Единое окно доступа к образовательным ресурсам. Доступ к интегральному каталогу образовательных интернет-ресурсов, электронной учебно-методической библиотеке для общего и профессионального образования и к ресурсам системы федеральных образовательных порталов - http://www.window.edu.ru.

Заключение

Данное учебное пособие предназначено для оказания помощи студентам при выполнении и защите ими лабораторных работ. В предложенном пособии рассмотрены наиболее часто используемые для решения прикладных задач математические методы и современные вычислительные средства их реализации. Рассмотрены возможности применения этих средств, в зависимости от поставленной задачи.

Пособие составлено в соответствии с читаемым на Механическом факультете и факультете Переработки природных соединений курсом «Математические методы в инженерии».

При составлении вариантов заданий авторы постарались учесть специфику этих факультетов и показать возможности применения математических методов для решения задач, связанных со специальными и общетехническими дисциплинами.

Изучение предложенных методов позволит студентам использовать их в дальнейшем при изучении специальных и общетехнических дисциплин, а также в научно-исследовательской работе.

Приложение А

(обязательное)

Таблица 1 - Встроенные операторы и функции MathCad

Функция	Аргументы	Описание
Given		Ключевое слово для ввода систем уравнений, неравенств и т.п.
Find(x1,x2,…)	(x1,x2) - переменные	Возвращает корень алгебраического уравнения (скаляр) или системы (вектор), определенный в блоке с ключевым словом Given
root(f(x),x,a,b)	f(x) − функция, x - переменная, (а, в) − интервал поиска корня	Возвращает корень функции
polyroots(v)	v - вектор, составленный из коэффициентов полинома	Возвращает вектор всех корней полинома
lsolve(A,b)	A -матрица СЛАУ, b - вектор правых частей уравнений	Решение системы линейных уравнений (СЛАУ)
Minimize(f, x1, x2, ...)	f(x1, x2, ...) − функция x1, x2, ...−аргументы, по которым произво­дится минимизация	Вектор значений аргументов, при которых функция f достигает минимума (возможно задание дополнительных условий в блоке с ключевым словом Given)

Продолжение таблицы 1

Maximize(f, x1, x2, ...)	f(x1, x2, ...) − функция x1, x2, ... − аргументы, по которым производится минимизация	Вектор значений аргументов, при которых функция f достигает максимума (возможно задание дополнительных условий в блоке с ключевым словом Given)
interp(s, x, y, t)	S - вектор производных второго порядка, y − вектор данных , t - аргумент	Сплайн-интерполяция
lspline(x,y)	x, y-векторы данных	Вектор коэффициентов линейного сплайна
cspline(x,y)	x, y-векторы данных	Вектор коэффициентов кубического сплайна
Odesolve(x,b,[ step])	x - переменная ин­тегрирования ОДУ b - конечная точка интервала интегри­рования step - число шагов интегрирования ОДУ	Возвращает функцию от х, которая является решением обыкно­венного дифференци­ального уравнения. Уравнения и началь­ные или краевые ус­ловия должны зада­ваться после ключе­вого слова Given, b – конечная точка ин­тервала интегрирова­ния, step – необяза­тельный параметр за­дающий количество шагов на интервале.

Окончание таблицы 1

rkfixed(y,x1, x2, npoints, D)	y − вектор начальных условий; (x1, x2) − интервал интегрирования, npoints – число шагов интегрирования D(x, y) − векторная функция, задающая систему ОДУ	Возвращает матрицу решений методом Рунге-Кутта системы ОДУ, правые части которых записаны в символьном векторе D, на интервале от х1 до х2 , с начальными данными у, и фикси­рованным числом шагов n.
Rkadapt(y,x1,x2, npoints, D)	y − вектор начальных условий (x1, x2) − интервал интегрирования npoints – число шагов интегрирования D(x,y) − векторная функция, задающая систему ОДУ	Возвращает мат­рицу, содержащую таблицу значений решения задачи Коши на интервале от х1 до х2 для системы ОДУ, вычисленную методом Рунге- Кута (с переменным ша­гом), правые части уравнений записаны в символьном векторе D, начальные данные в векторе - число npoints размер шага.
Bulstoer(y, x1, x2, npoints, D)	y − вектор начальных условий (x1, x2) − интервал интегрирования npoints – число шагов интегрирования D(x,y) − векторная функция, задающая систему ОДУ	Матрица решения системы ОДУ, правая часть которых запи­сана в символьном векторе D, заданными начальными усло­виям в векторе у на интервале (х1, х2) ис­пользуется метод Бу­лирш-Штера
ТOL	Специальная системная переменная для контроля погрешности вычислений, параметр, определяющий условие прекращения итераций

Приложение В

(справочное)

Перечень ключевых слов

Алгебраические уравнения и системы в среде Mathcad	Линейная оптимизация в Excel и Mathcad
Аналитические вычисления в Mathcad	Линейные дифференциальные уравнения
Виды массивов в Mathcad	Метод наименьших квадратов
Графический метод поиска экстремума	Матрицы в среде Mathcad
Градиентный метод	Метод Рунге-Кутта
Графический метод решения ЗЛП	Оценки в задачах ЛП
Графики в Mathcad и Excel	Построение линии тренда в Excel
Дифференциальные модели	Решение дифференциальных уравнений в Mathcad
Задача ЛП	Симплекс – метод
Задача Коши	Составление моделей
Задачи нелинейной оптимизации	Статические и динамические модели физических процессов и инженерных систем
Интерполяционный полином Лагранжа	Устойчивость решений задач ЛП
Интерполяционный полином Ньютона	Устойчивость решений задач ЛП
Каноническая форма ЗЛП	Функции двух переменных в среде Mathcad
Класс задач линейного программирования	Целочисленные задачи ЛП
Краевая задача	Экстремум функции одной переменной в среде Mathcad
Критерий оптимальности	Экстремум функции нескольких переменных