Редуцированное устройство идентификации

Для 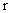— мерного вектора выходных сигналов 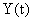достаточно синтезировать устройство идентификации размерности 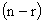, характеризуемое вектором состояния такой же размерности. Пусть исследуемый объект управления или механизм представляются системой дифференциальных уравнений вида

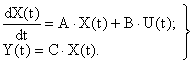(3)

При этом r выходов объекта линейно независимы, что эквивалентно тому, что ранг матрицы 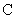равен r. Тогда оценку всего вектора 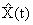можно получить из уравнения

.

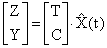Из этого уравнения вытекает выражение для определения оценки вектора состояния исследуемой системы, которая имеет вид

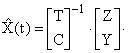
Вектор состояния исследуемой системы можно представить как

,

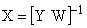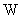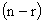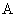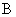где – вектор неизмеряемых переменных состояния исследуемой системы размерностью . Разбивая матрицы и системы уравнений (3) получаем систему уравнений

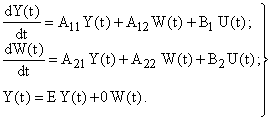
Из этих уравнений получается уравнение наблюдающего устройства идентификации, которое принимает вид

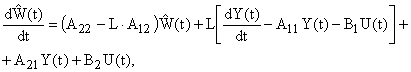(4)

где 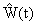— вектор выхода наблюдающего устройства размерностью 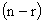, 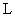– матрица, определяющая расположение корней характеристического полинома наблюдающего устройства.

Структурная схема, наблюдающего устройства, построенного на базе уравнения (4), представлена на рис. 3.

Операции дифференцирования вектора измеряемых переменных наблюдаемого устройства можно избежать, если использовать преобразованное уравнение вида (4). Такое устройство идентификации называют наблюдающим устройством типа 2. Оно базируется на уравнении вида

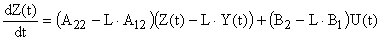(5)

где 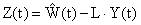— вектор состояния наблюдающего устройства типа 2.

Использование уравнения (5) аналогично переносу точки суммирования с входа интегратора на его выход. В результате структурная схема наблюдающего устройства идентификации типа 2 принимает вид, представленный на рис. 4.

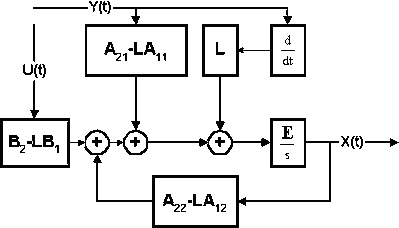
Рис. 3. Схема редуцированного устройства идентификации, использующего производные измеряемых координат

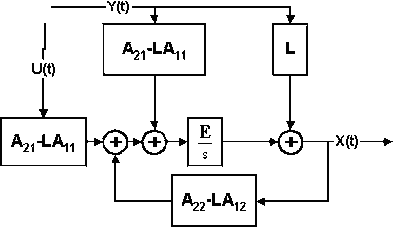
Рис. 4. Структурная схема редуцированного наблюдающего устройства второго типа

Общий алгоритм синтеза редуцированного устройства выглядит следующим образом:

1. Проверка наблюдаемости исходной системы по рангу матрицы ее наблюдаемости.

2. Определение корней характеристического многочлена матрицы А.

3. Выбор матрицы 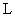, корни характеристического полинома которой обеспечивают окончание переходных процессов в устройстве идентификации за требуемое время.

4. Определение параметров матриц взаимодействия устройства идентификации с наблюдаемой системой.

Полученные соотношения для определения структуры и параметров наблюдающих устройств позволяют получить величины компонент вектора состояния системы управления, непосредственное измерение которых не представляется возможным. Их использование позволяет расширить возможности систем управления различными управляемыми механизмами.

Рассмотрим процедуру синтеза наблюдающих устройств на примере двигателя постоянного тока. Основной целью создания устройства идентификации является определение величины электромагнитного момента, развиваемого двигателем постоянного тока, структурная схема которого представлена на рис.5.

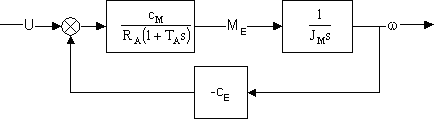
Рис. 5. Структурная схема двигателя постоянного тока

За составляющие вектора состояния САУ принимаем угловую скорость его вала 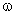и величину развиваемого электромагнитного момента 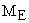, которая пропорциональна току, потребляемому якорной обмоткой двигателя. Исходя из структурной схемы объекта получаем следующие уравнения, которые описывают его поведение в переменных состояния

,

.

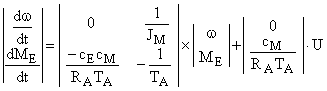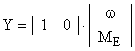Так как выход рассматриваемого устройства является скалярной величиной, то матрица 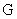, характеризующая вход устройства идентификации, имеет вид

.

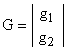Тогда матрица синтезируемого устройства идентификации принимает следующий вид:

,

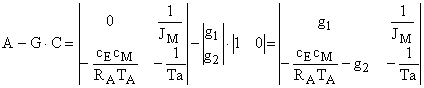а характеристический полином наблюдающего устройства описывается выражением

.

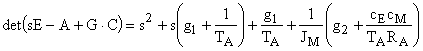Предполагаем, что для устройства идентификации желателен корень 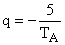, кратность которого равна 2. При этом желаемый характеристический полином наблюдающего устройства принимает вид, соответствующий биноминальному распределению корней

.

Приравнивая коэффициенты характеристического уравнения наблюдающего устройства к желаемым значениям, получаем

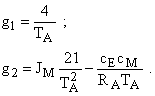
Зададим характеристики устройства идентификации электромагнитного момента для двигателя постоянного тока типа ПБВ100М со следующими параметрами:

· номинальной частотой вращения ,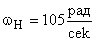

· номинальным напряжением питания ,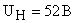

· номинальным током якоря 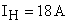=18 A,

· сопротивлением якорной обмотки ,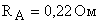

· моментом инерции якоря ,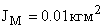

· электромагнитной постоянной времени якорной обмотки ,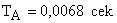

· конструктивными коэффициентами .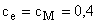

Устройство идентификации электромагнитного момента для такого двигателя описывается уравнением вида

.

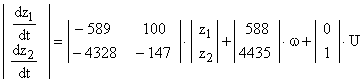На рис.6 представлена структурная схема двигателя с наблюдающим устройством, предназначенным для определения электромагнитного момента, развиваемого двигателем.

Продолжим рассмотрение системы управления с двигателем постоянного тока. Он представляет собой систему второго порядка с одним измеряемым выходным сигналом – угловой скоростью. Для получения оценки второй переменной состояния, а именно развиваемого двигателем электромагнитного момента, произведем синтез редуцированного устройства идентификации, порядок которого равен единице.

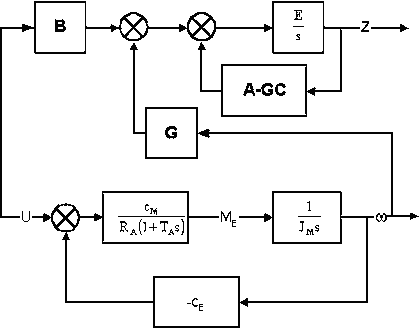
Рис.6. Структурная схема двигателя и устройства идентификации Льюинбергера

На основании коэффициентной матрицы объекта находим, что

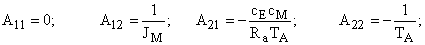
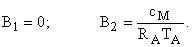
Будем считать, что редуцированное устройство идентификации имеет те же собственные значения, что и рассмотренное выше наблюдающее устройство. Для выполнения этого условия необходимо задать матрицу 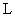вида

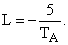
Принимая во внимание схему редуцированного устройства идентификации, представленную на рис. 3, передаточные функции звеньев этой системы можно найти как

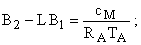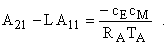(6)

Исходя из полученных выражений получается схема электродвигателя постоянного тока с устройством идентификации, которая показана на рис.7.

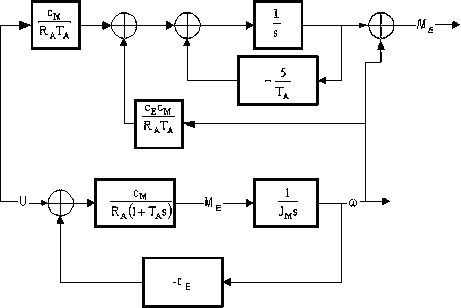
Рис.7. Структурная схема двигателя и редуцированного устройства идентификации электромагнитного момента

Процесс отработки изменения напряжения на якоре двигателя показан на рис. 8. Оценка вычисленного значения момента для всех 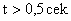практически совпадает с искомыми значениями моделируемой координаты.

Рис.8. График отработки единичного скачка напряжения, подаваемого на якорь электродвигателя

Наблюдающее устройство может использоваться для построения систем регулирования угловой скорости вала двигателя постоянного тока, базирующихся на принципах подчиненного или модального управления. При этом вычисленная величина электромагнитного момента обеспечивает получение дополнительной информации о состоянии управляемого объекта.

На рис. 9 представлена полная схема системы модального управления двигателем постоянного тока. Для определения параметров обратных связей по току 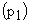и скорости 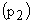используется выражение (6). Стандартный вид характеристического полинома при биноминальном распределении корней для объекта управления второго порядка имеет вид

.

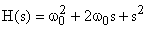Характеристический полином управляемого объекта

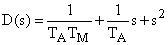(7)

Коэффициенты матрицы-столбца передаточных функций двигателя имеют вид

.

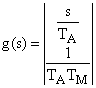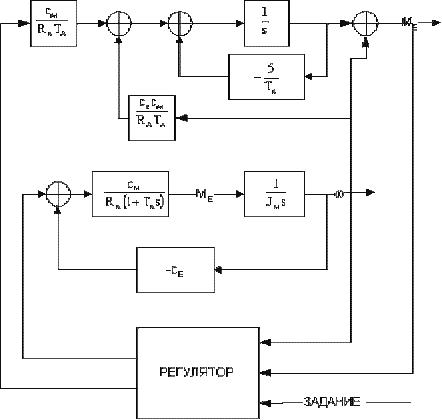
Рис. 8. Структурная схема САУ с наблюдающим устройством

Тогда выражение, определяющее распределение корней характеристического уравнения САУ, можно представить в виде

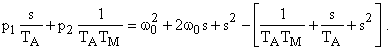
Решая это уравнение относительно коэффициентов матрицы обратных связей системы, получаем, что

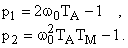
Из двух переменных, использованных для оценки состояния объекта, непосредственному измерению доступна лишь угловая скорость двигателя.

Для оценки величины электромагнитного момента двигателя используется наблюдающее устройство.

Полученные соотношения определяют параметры регулятора угловой скорости двигателя постоянного тока.