Интегральное регулирование по второму интегралу от ошибки

Двойной интегральный закон регулирования имеет вид:

u(t) = W_рег(p) x(t) = k₃/p² x(t) ,

тогда в разомкнутом состоянии система будет характеризоваться ПФ:

W(p) = W_рег(p) W_o(p) = k₃/p² W_o(p) .

В этом случае система будет обладать астатизмом второго порядка - в ноль обратятся как постоянная составляющая ошибки, так и её скоростная составляющая (ошибка от помехи здесь не рассматривается):

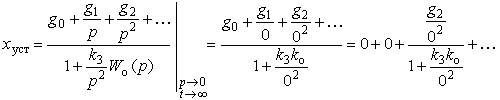
Резюме: повышение порядка астатизма приводит к увеличению установившейся точности САР, но делает систему более замедленной в действии.

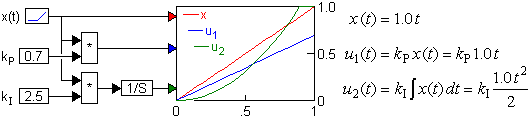
На рисунке показано, что, на сколько бы мал ни был коэффициент усиления пропорционального канала, и насколько большим бы ни был коэффициент усиления интегрального канала, для малых отклонений ошибки x(t) сигнал управления на объект u(t) интегральным каналом формируется менее интенсивно.

Изодромное регулирование - PI

Изодромный закон регулирования имеет вид:

u(t) = W_рег(p) x(t) = (k₁ + k₂/p) x(t) ,

тогда в разомкнутом состоянии система будет характеризоваться ПФ:

W(p) = W_рег(p) W_o(p) = (k₁ + k₂/p) W_o(p) .

В этом случае если p®0, то W(p)®¥ и регулирование будет астатическим. Но если p®¥, то W(p)®k₁k_o=k и регулирование будет пропорциональным.

Резюме: PI-регулирование сочетает точность I-регулирования и быстродействие P-регулирования.

Регулирование с использованием производных

Регулирование с использованием одного канала, чувствительного к производной сигнала не имеет самостоятельного значения, т.к. сигнал управления:

u(t) = W_рег(p) x(t) = k₄ p x(t) ,

будет равен нулю при p®0 (т.е. в установившемся режиме). Поэтому обязательно наличие параллельного либо P, либо I-канала, а чаще обоих:

u(t) = (k₁ + k₂/p + k₄ p) x(t) .

Резюме: В таком варианте регулятора управляющее воздействие будет образовываться даже когда x(t)=0, но dx/dt¹0. Т.е. наличие параллельного D-канала в регуляторе повышает быстродействие системы и снижает ошибки в динамике.

Сегодня техническая реализация регуляторов, чувствительных к производным более высоких порядков, затруднена.

Устойчивость САУ

Понятие устойчивости системы регулирования связано с ее способностью возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния.

Основы теории устойчивости САУ были заложены А.М. Ляпуновым в его работе "Общая задача устойчивости движений", опубликованной в 1882 г.

В статическом режиме работы все составляющие вектора состояния САУ не зависят от момента времени их рассмотрения и остаются постоянными, соответствующими условию равновесия системы. Это состояние в зависимости от структуры и параметров САУ может быть устойчивым или неустойчивым.

Если после изменения вектора внешних воздействий система приходит в состояние, при котором все составляющие вектора ее состояния становятся постоянными, то есть система возвращается в положение равновесия, то это состояние равновесия является устойчивым.

В случае, когда после изменение входного сигнала или возмущения, система не стремится в первоначальное состояние, а вектор выходных сигналов изменяется независимо от внешнего воздействия, то такое состояние является неустойчивым. В этом случае система автоматического управления является неустойчивой. Графическая интерпретация таких режимов работы САУ представлена на рис.

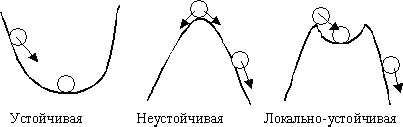
Рис. Графическая интерпретация устойчивости.

Под устойчивостью понимается свойство САУ возвращаться в исходное состояние после вывода ее из этого состояния и прекращения влияния задающего или возмущающего воздействия.

Только устойчивая система автоматического управления может выполнять возложенные на нее функции. Поэтому одной из основных задач САУ является обеспечение ее устойчивости.

Если САУ представляется системой линейных дифференциальных уравнений, то ее устойчивость не зависит от величины и точки приложения внешних возмущений.

Нелинейные системы могут быть устойчивы при малых возмущениях и неустойчивы при больших возмущениях. Теорема Ляпунова устанавливает, что об устойчивости нелинейных систем при малых возмущениях можно судить по их линеаризованным уравнениям, достаточно адекватно описывающих поведение САУ при малых отклонениях от положения равновесия. Поэтому будем рассматривать только вопросы устойчивости САУ, представляемых линейными или линеаризованными дифференциальными уравнениями.