Закоопределенность квадратичной формы. Критерий Сильвестра
Матрицы и операции над ними.
Матрица — математический объект, записываемый в виде прямоугольной таблицы элементов, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы.
Операции: сложение матриц
умножение матрицы на число
транспонирование
перемножение двух матриц
возведение в степень
Определители и их свойства.
Любой квадратной матрице можно поставить в соответствие некоторое число – определитель
Минор – определитель, получ если в исходной матрице вычеркнуть строку и столбец, на пересеч к-ых находится этот элемент
Теорема о разложении определителя по элементам строки: определитель равен сумме произведений элементов строки (столбца) на их алгебраические дополнители
Алгебраические дополнители:

Свойства определителей:
· При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится
· Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.
· Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.
· Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).
· Общий множитель элементов какой-либо строки определителя можно вынести за знак определителя.
· Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.
· Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.
Системы линейных алгебраических уравнений.
Общий вид СЛАУ:

Исследование систем линейных алгебраических уравнений методом Крамера и методом Гаусса.
Метод Крамера:  , столбец с номером j,
, столбец с номером j,
1сл: если ∆≠0, то единственное решение
 - формула Крамера
- формула Крамера
2сл: если ∆=0 и все  =0, то бесконечно много решений
=0, то бесконечно много решений
3сл: если ∆=0, но хотя бы один  ≠0, то нет решений, или система несовместна
≠0, то нет решений, или система несовместна
Метод Гаусса:
· составить расширенную матрицу системы,
· путем преобразований привести матрицу к ступенчатому виду,
· определить ранг начальной матрицы и итоговой:
если r(A)=r(A|B), то матрица совместна и есть решения
если r(A)≠r(A|B), то матрица несовместна, => решений нет
Квадратичные формы и их матрицы.
Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора.
– по главной диагонали расп числа при квадратах
– на побочных диагоналях расп половины коэффициентов при произведениях
 ,
,
=> А= 
Закоопределенность квадратичной формы. Критерий Сильвестра.
Кв-я форма может быть: положительно- или отрицательно- определенной, или не быть знакоопределенной; Для того, чтобы кв-я форма была положит-/отрицат- определенной, необходимо, чтобы все соотв значения матрицы А были положит/отрицат
Критерий Сильвестра: главные (угловые) миноры кв-ой матрицы:
· если все Mj>0, то положит определенная
· если  <0,
<0,  >0,
>0,  <0 (чередуются, начиная с <), то отрицат определеная
<0 (чередуются, начиная с <), то отрицат определеная
· если не выполняются ни 1-е, ни 2-е условия, то форма не явл знакоопределенной
Прямая на плоскости.
ü Общее ур-ние прямой: Ах+Ву+С=0, где А и В ≠0 одновременно,
ü Ур-ние прямой «в отрезках»:
ü  , где a≠0 и b≠0
, где a≠0 и b≠0
ü Ур-ние пучка прямых: у-  =k(x-
=k(x- 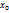 )
)
ü Угол между двумя прямыми: tgɥ=|  |
|
– усл || двух прямых:  =
=  (пр-е ||, если их угл коэф равны)
(пр-е ||, если их угл коэф равны)
– усл ⊥ двух прямых: 
ü Ур-е прямой, проход через заданную точку, ⊥ -M(  , n(A, B):
, n(A, B):  -
- 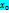 )+B(y-
)+B(y-  )=0
)=0
ü Каноническое ур-е: M(  , γ(l, m) - (направляющий вектор ||):
, γ(l, m) - (направляющий вектор ||): 
ü Ур-е прямой, проход через две точки: 
ü Расстояние от точки до прямой:  , L:Ax+By+C=0;
, L:Ax+By+C=0;

