Задачи для самостоятельного решения. 1. Фирма-поставщик в рекламном буклете утверждает, что средний срок безотказной работы

1. Фирма-поставщик в рекламном буклете утверждает, что средний срок безотказной работы предлагаемого изделия — 2900 ч. Для выборки из 50 изделий средний срок безотказной работы оказался равным 2720 ч при выборочном среднем квадратичном отклонении 700 ч. При 5% -м уровне значимости проверить гипотезу о том, что значение 2900 ч является математическим ожиданием.

2. Составлена случайная выборка из 64 покупателей, которые интересовались товаром А. Из них товар А купили 16 человек. Поставщик утверждает, что данный товар должен привлечь треть покупателей, а среднее квадратичное отклонение равно одному человеку. Проверить нулевую гипотезу при 5%-м уровне значимости.

3. Средний диаметр подшипников должен составлять 35 мм. Однако для выборки из 82 подшипников он составил 35,3 мм при выборочном среднем квадратичном отклонении 0,1мм. При 5%-м уровне значимости проверить гипотезу о том, что станок, на котором изготавливают подшипники, не требует подналадки.

4. Поставщик удобрений утверждает, что применение новой партии удобрений обеспечивает урожайность пшеницы в 60 ц/га. Удобрения внесли на площади в 37 га и получили урожай 55 ц/га при выборочном среднем квадратичном отклонении 3 ц/га. При 5% -м уровне значимости оценить справедливость утверждения поставщика.

5. Среднесуточная продажа хлеба в течение многих лет для данного магазина составляла 6 т при среднем квадратичном отклонении 0,05 т. Сегодня магазином было продано 7 т хлеба. Можно ли при 5%-м уровне значимости предполагать, что и завтра будет продано 7 т хлеба?

6. Фирма — изготовитель женских украшений, выпустив новый товар, утверждает, что 40% покупателей купят эти украшения. В ходе 10-дневной рекламной распродажи в среднем приобрели украшения 29,5% покупателей, выборочное среднее квадратичное отклонение составило 16,5% . При 5%-м уровне значимости оценить утверждение изготовителя товара.

7. Поставщик двигателей утверждает, что средний срок их службы равен 800 ч. Для выборки из 17 двигателей средний срок службы оказался равным 865 ч при выборочном среднем квадратичном отклонении 120 ч. Проверить нулевую гипотезу при уровне значимости: а) 5% ; б) 1% .

8. По результатам 10 замеров установлено, что среднее время обслуживания мастером клиента 15 мин.. Предполагая, что время обслуживания клиента — нормально распределенная случайная величина с дисперсией 9 мин², при уровне значимости 0,05 установить, можно ли принять в качестве норматива (математического ожидания) для обслуживания одного клиента: а) 21 мин; б) 16 мин.

9. По паспортным данным на автомобильный двигатель, расход топлива на 100 км пробега составляет 10 л при среднем квадратичном отклонении 2 л. В результате совершенствования конструкции ожидается, что расход топлива уменьшится. Для проверки проведены испытания 25 случайно отобранных автомобилей с модернизированным двигателем: средний расход топлива на 100 км пробега составил 9,2 л. Используя 5%-й уровень значимости, проверить гипотезу, утверждающую, что модернизация повлияла на расход топлива.

10. Из большой партии ананасов одного размера случайным образом отобрано 36 штук. Выборочная средняя масса одной штуки при этом оказалась равной 930 г. Используя двусторонний критерий при 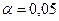, проверить гипотезу, что средняя масса одного ананаса (по утверждению поставщика) составляет 1 кг, если:

а) средне квадратическое отклонение известно и составляет 200 г;

б) средне квадратическое отклонение неизвестно, а выборочное составило 250 г.

11. Срок хранения продукции, изготовленной по технологии А, составил:

Срок хранения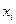
Число единиц продукции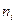

а изготовленной по технологии В:

Срок хранения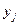
Число единиц продукции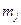

Предположив, что случайные величины X и Y распределены по нормальному закону, проверить гипотезу о равенстве дисперсий при уровне значимости 0,1 и альтернативной гипотезе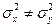

12. Температура в холодильной камере контролируется по двум электронным термометрам. Для сравнения точности термометров их показания фиксируются одновременно. Проведено 10 замеров показаний термометров:

Номер замера
Термометр 1	-7,11	-8,63	-6,89	-7,23	-7,51	-7,68	-7,91	-6,97	-7,44	-7,64
Термометр 2	-7,13	-8,49	-7,12	-7,19	-7,67	-7,49	-8,03	-7,15	-7,29	-7,89

При уровне значимости 0,1 проверить гипотезу о равенстве дисперсий.

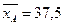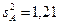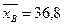13. На двух станках производят одну и ту же продукцию, контролируемую по наружному диаметру изделия. Из продукции станка А было проверено 16 изделий, а из продукции станка В — 25 изделий. Выборочные оценки математических ожиданий и дисперсий контролируемых размеров составили мм при мм² и мм при 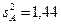мм². Проверить гипотезу о равенстве дисперсий, если .

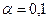14. Фирма поставляет радары для измерения скорости движения автомобилей. Для закупки большой партии проведены испытания приборов, изготовленных на заводе А и на заводе В. Измерения проводили на одной и той же машине и на одной и той же дороге. Определены величины отклонений между показаниями спидометра автомобиля и радара:

Завод А

Отклонение, км/ч		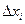-0,7	-0,3	-0,1	0,5	0,8	0,9	1,0	1,2	1,3
Число измерений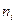

Завод В

Отклонение, км/ч		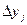-0,6	-0,1	0,4	0,7	1,0	1,4
Число измерений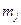

Полагая показания спидометра автомобиля эталоном, проверить гипотезу об одинаковой точности измерений, проводимых радарами завода А и завода В, при уровне значимости 0,1.

15. Средний ежедневный объем продаж за I квартал текущего года для 17 торговцев района А составляет 15 тыс. руб. при «исправленном» среднем квадратичном отклонении 2,5 тыс. руб., а для 10 торговцев района В — 13 тыс. руб. при «исправленном» среднем квадратичном отклонении 3 тыс. руб. Каждую группу можно считать случайной независимой выборкой из большой совокупности. Существенно ли различие объемов продаж в районах А и В при 5% -м уровне значимости?

16. Вусловиях задачи 15 выяснить, существенно ли при 5% -м уровне значимости превышение объема продаж в районе А по сравнению с объемом в районе В.

17. Акционерное общество (АО) выпускает печенье «Русские узоры» в пачках, на которых написано: масса нетто 200 г. Осуществлена выборка для оценки средней массы печенья в пачках, выпущенных московской и санкт-петербургской фабриками АО. Результаты выборок таковы (указана масса пачек печенья «Русские узоры»):

Московская фабрика:

201, 195, 197, 199, 202, 198, 199, 203, 195, 196, 198, 199,194, 203, 195, 202, 197

Санкт-петербургская фабрика:

203, 207, 191, 193, 197, 201, 196, 192, 194, 195, 198, 196

Предполагая, что случайная величина массы пачки печенья распределена по нормальному закону с одинаковыми дисперсиями, и считая выборки независимыми, определить:

а) средние выборочные и «исправленные» средние квадратичные отклонения массы для каждой фабрики;

б) для 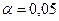значимо или нет различие между средними выборочными (если это различие имеется);

в) является ли величина 200 г математическим ожиданием массы при 5%-м уровне значимости?

18. Расход сырья на единицу продукции составил: по старой технологии

Расход сырья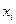
Число изделий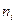

по новой технологии

Расход сырья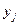
Число изделий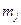

Предположив, что соответствующие случайные величины X и Y имеют нормальные распределения с математическими ожиданиям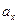и и 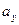и одинаковыми дисперсиями, проверить:

а) при уровне значимости 0,1 гипотезу : 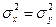при альтернативной : ;

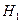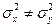б) при уровне значимости 0,05 гипотезу : 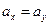при альтернативной : .

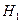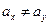19. Производительность каждого из агрегатов А и В составила (в кг вещества за час работы):

Номер замера
Агрегат А	14,1	13,1	14,7	13,7	14,0
Агрегат В	14,0	14,5	13,7	12,7	14,1

Можно ли считать производительность агрегатов А и В одинаковой в предположении, что обе выборки получены из нормально распределенных генеральных совокупностей, при уровне значимости ?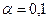

20. Фирма предлагает автоматы по розливу напитков. При выборке 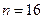найдена средняя величина 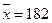г дозы, наливаемой в стакан автоматом № 1. По выборке 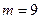найдена средняя величина 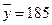г дозы, наливаемой в стакан автоматом № 2. По утверждению изготовителя, случайная величина наливаемой дозы имеет нормальный закон распределения с дисперсией, равной 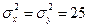г². Можно ли считать отличия выборочных средних случайной ошибкой при уровне значимости ?

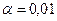21. В таблице приведены результаты измерения процентного содержания крахмала в картофеле (исследовали 16 клубней различных сортов картофеля) двумя различными способами:

№

I

II

При уровне значимости 0,1 можно ли считать, что крахмалистость картофеля одна и та же для обоих способов?

22. Используются два вида удобрений: I и II. Для сравнения их эффективности были попарно выбраны 20 участков равной площади так, что пару составили участки, однородные по плодородию. Десять участков были обработаны удобрением I, а десять, парных им, — удобрением II. На соответствующих парах участков получили следующий урожай:

№
I	8,0	8,4	8,0	6,4	8,6	7,7	7,7	5,6	5,6	6,2
II	5,6	7,4	7,3	6,4	7,5	6,1	6,6	6,0	5,5	5,0

При уровне значимости 5% проверить гипотезу о различном влиянии использования удобрения I или П.

23. Экзаменационный билет по математике содержит 10 заданий. Пусть — случайная величина числа задач, решенных абитуриентами на вступительном экзамене. Результаты сдачи экзамена по математике для 300 абитуриентов таковы:

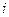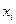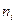Оценить закон распределения случайной величины X.

24. Коммерсант предполагает, что объем продаж нового вида продукции в каждой из пяти торговых точек, расположенных в различных районах, будет одинаков. Фактический объем продаж оказался разным:

Район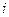
Фактический объем продаж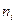

Оценить, значимы или нет различия между наблюдаемыми и ожидаемыми объемами продаж при уровне значимости 0,01 и 0,05.

25. Результаты взвешивания 50 случайным образом отобранных пачек чая приведены ниже (в граммах):

150, 147, 152, 148, 149, 153, 151, 150, 149, 147, 153, 151, 152, 151, 149, 152, 150, 148, 152, 150, 152, 151, 148, 151, 152, 150, 151, 149, 148, 149, 150, 150, 151, 149, 151, 150, 151, 150, 149, 148, 147, 153, 147, 152, 150, 151, 149, 150, 151, 153.

Оценить закон распределения случайной величины X — массы пачки чая — для уровня значимости .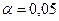

26. Страховая компания выпустила четыре вида страховых полисов в предположении, что спрос на них будет одинаков. Фактические объемы реализации различных видов страховых полисов приведены ниже:

Виды страховых полисов	А	В	С	D
Фактический объем реализации

Оценить для уровней значимост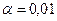и и 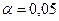, согласуется ли фактический и теоретический спрос на различные виды страховых полисов.

27. Результаты исследования числа покупателей в универсаме в зависимости от времени работы приведены ниже:

Часы работы	9—10	10—11	11—12	12—13
Число покупателей

Можно ли утверждать при уровне значимости 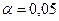, что случайная величина X — число покупателей — подчинена нормальному закону?

28. Дано следующее распределение успеваемости 125 студентов, сдавших три экзамена:

Число сданных экзаменов
Число студентов

Проверить гипотезу о биномиальном распределении числа сданных экзаменов при .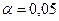

29. Масса (в граммах) произвольно выбранных 30 пачек полуфабриката «Геркулес» такова:

503, 509, 495, 493, 489, 485, 507, 511, 487, 495, 506, 504, 507, 511, 499, 491, 494, 518, 506, 515, 487, 509, 507, 488, 495, 490, 498, 497, 492, 495.

Можно ли при уровне значимости 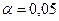утверждать, что случайная величина X — масса пачки — подчинена нормальному закону распределения?

30. При принятии на работу фирма предлагает 4 теста. Результаты решения этих тестов десятью претендентами приведены ниже:

Число верно решенных тестов
Число участников

Проверить гипотезу о биномиальном распределении случайной величины X — числа успешно решенных тестов — при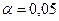

Приложения

Приложение 1

Таблица значений функции Лапласа

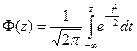
Z	0,09	0,08	0,07	0,06	0,05	0,04	0,03	0,02	0,01	0,00
-3,5	0,00017	0,00017	0,00018	0,00019	0,00020	0,00020	0,00021	0,00022	0,00022	0,00023
-3,4	0,00024	0,00025	0,00026	0,00027	0,00028	0,00029	0,00030	0,00031	0,00033	0,00034
-3,3	0,00035	0,00036	0,00038	0,00039	0,00040	0,00042	0,00043	0,00045	0,00047	0,00048
-3,2	0,00050	0,00052	0,00054	0,00056	0,00058	0,00060	0,00062	0,00064	0,00066	0,00069
-3,1	0,00071	0,00074	0,00076	0,00079	0,00082	0,00085	0,00087	0,00090	0,00091	0,00097
-3,0	0,00100	0,00104	0,00107	0,00111	0,00114	0,00118	0,00122	0,00126	0,00131	0,00135
-2,9	0,00140	0,00140	0,00150	0,00150	0,00160	0,00160	0,00170	0,00170	0,00180	0,00190
-2,8	0,00190	0,00200	0,00210	0,00210	0,00220	0,00230	0,00230	0,00240	0,00250	0,00260
-2,7	0,00260	0,00270	0,00280	0,00290	0,00300	0,00310	0,00320	0,00330	0,00340	0,00350
-2,6	0,00360	0,00370	0,00380	0,00390	0,00400	0,00410	0,00430	0,00440	0,00450	0,00470
-2,5	0,00480	0,00490	0,00510	0,00520	0,00540	0,00550	0,00570	0,00590	0,00600	0,00620
-2,4	0,00640	0,00660	0,00680	0,00690	0,00710	0,00730	0,00750	0,00780	0,00800	0,00820
-2,3	0,00840	0,00870	0,00890	0,00910	0,00940	0,00960	0,00990	0,01020	0,01040	0,01070
-2,2	0,01100	0,01130	0,01160	0,01190	0,01220	0,01250	0,01290	0,01320	0,01360	0,01390
-2,1	0,01430	0,01460	0,01500	0,01540	0,01580	0,01620	0,01660	0,01700	0,01740	0,01790
-2,0	0,01830	0,01880	0,01920	0,01970	0,02020	0,02070	0,02120	0,02170	0,02220	0,02280
-1,9	0,02330	0,02390	0,02440	0,02500	0,02560	0,02620	0,02680	0,02740	0,02810	0,02870
-1,8	0,02940	0,03010	0,03070	0,03140	0,03220	0,03290	0,03360	0,03440	0,03510	0,03590
-1,7	0,03670	0,03750	0,03840	0,03920	0,04010	0,04090	0,04180	0,04270	0,04360	0,04460
-1,6	0,04550	0,04650	0,04750	0,04850	0,04950	0,05050	0,05160	0,05260	0,05370	0,05480
-1,5	0,05590	0,05710	0,05820	0,05940	0,06060	0,06180	0,06300	0,06430	0,06550	0,06680
-1,4	0,06810	0,06940	0,07080	0,07210	0,07350	0,07490	0,07640	0,07780	0,07930	0,08080
-1,3	0,08230	0,08380	0,08530	0,08690	0,08850	0,09010	0,09180	0,09340	0,09510	0,09680
-1,2	0,09850	0,10030	0,10200	0,10380	0,10570	0,10750	0,10930	0,11120	0,11310	0,11510
-1,1	0,11700	0,11900	0,12100	0,12300	0,12510	0,12710	0,12920	0,13140	0,13350	0,13570
-1,0	0,13790	0,14010	0,14230	0,14460	0,14690	0,14920	0,15150	0,15390	0,15620	0,15870
-0,9	0,16110	0,16350	0,16600	0,16850	0,17110	0,17360	0,17620	0,17880	0,18140	0,18410
-0,8	0,18670	0,18940	0,19220	0,19490	0,19770	0,20050	0,20330	0,20610	0,20900	0,21190
-0,7	0,21480	0,21770	0,22070	0,22360	0,22660	0,22970	0,23270	0,23580	0,23890	0,24200
-0,6	0,24510	0,24830	0,25140	0,25460	0,25780	0,26110	0,26430	0,26760	0,27090	0,27430
-0,5	0,27760	0,28100	0,28430	0,28770	0,29120	0,29460	0,29810	0,30150	0,30500	0,30850
-0,4	0,31210	0,31560	0,31920	0,32280	0,32640	0,33000	0,33360	0,33720	0,34090	0,34460
-0,3	0,34830	0,35200	0,35570	0,35940	0,36320	0,36690	0,37070	0,37450	0,37830	0,38210
-0,2	0,38590	0,38970	0,39360	0,39740	0,40130	0,40520	0,40900	0,41290	0,41680	0,42070
-0,1	0,42470	0,42860	0,43250	0,43640	0,44040	0,44430	0,44830	0,45220	0,45620	0,46020
-0,0	0,46410	0,46810	0,47210	0,47610	0,48010	0,48400	0,48800	0,49200	0,49600	0,50000

Z	0,00	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
+0,0	0,50000	0,50400	0,50800	0,51200	0,51600	0,51990	0,52390	0,52790	0,53190	0,53590
+0,1	0,53980	0,54380	0,54780	0,55170	0,55570	0,55960	0,56390	0,56750	0,57140	0,57530
+0,2	0,57930	0,58320	0,58710	0,59100	0,59480	0,59870	0,60260	0,60610	0,61030	0,61410
+0,3	0,61790	0,62170	0,62550	0,62930	0,63310	0,63680	0,64060	0,64430	0,64800	0,65170
+0,4	0,65540	0,65910	0,66280	0,66640	0,67000	0,67360	0,67720	0,68080	0,68440	0,68790
+0,5	0,69150	0,69500	0,69850	0,70190	0,70540	0,70880	0,71230	0,71570	0,71900	0,72240
+0.6	0,72570	0,72910	0,73240	0,73570	0,73890	0,74220	0,74540	0,74860	0,75170	0,75490
+0,7	0,75800	0,76110	0,76420	0,76730	0,77040	0,77340	0,77640	0,77910	0,78230	0,78520
+0,8	0,78810	0,79100	0,79390	0,79670	0,79950	0,80230	0,80510	0,80790	0,81060	0,81330
+0,9	0,81560	0,81860	0,82120	0,82380	0,82640	0,82890	0,83150	0,83400	0,83650	0,83890
+1,0	0,84130	0,84380	0,84610	0,84850	0,85080	0,85310	0,85540	0,85770	0,85990	0,86210
+1,1	0,86430	0,86650	0,86860	0,87080	0,87290	0,87490	0,87700	0,87900	0,88100	0,88300
+1,2	0,88490	0,88690	0,88880	0,89070	0,89250	0,89440	0,89620	0,89800	0,89970	0,90150
+1,3	0,90320	0,90490	0,90660	0,90820	0,90990	0,91150	0,91310	0,91470	0,91620	0,91770
+1,4	0,91920	0,92070	0,92220	0,92360	0,92510	0,92650	0,92790	0,92920	0,93060	0,93190
+1,5	0,93320	0,93450	0,93570	0,93700	0,93820	0,93940	0,94060	0,94180	0,94290	0,94410
+1,6	0,94520	0,94630	0,94740	0,94840	0,94950	0,95050	0,95150	0,95250	0,95350	0,95450
+1,7	0,95540	0,95640	0,95730	0,95820	0,95910	0,95990	0,96080	0,96160	0,95250	0,96330
+1,8	0,96410	0,96490	0,96560	0,96640	0,96710	0,96780	0,96860	0,96930	0,96990	0,97060
+1,9	0,97130	0,97190	0,97260	0,97320	0,97380	0,97440	0,97500	0,97560	0,97610	0,97670
+2,0	0,97730	0,97780	0,97830	0,97880	0,97930	0,97980	0,98030	0,98080	0,98120	0,98170
+2,1	0,98210	0,98260	0,98300	0,98340	0,98380	0,98420	0,98460	0,98500	0,98540	0,98570
+2,2	0,98610	0,98640	0,98680	0,98710	0,98750	0,98780	0,98810	0,98840	0,98870	0,98900
+2,3	0,98930	0,98960	0,98980	0,99010	0,99040	0,99060	0,99090	0,99110	0,99130	0,99160
+2,4	0,99180	0,99200	0,99220	0,99250	0,99270	0,99290	0,99310	0,99320	0,99340	0,99360
+2,5	0,99380	0,99400	0,99410	0,99430	0,99450	0,99460	0,99480	0,99490	0,99510	0,99520
+2,6	0,99530	0,99550	0,99560	0,99570	0,99590	0,99600	0,99610	0,99620	0,99630	0,99640
+2,7	0,99650	0,99660	0,99670	0,99680	0,99690	0,99700	0,99710	0,99720	0,99730	0,99740
+2,8	0,99740	0,99750	0,99790	0,99770	0,99770	0,99780	0,99790	0,99790	0,99800	0,99810
+2,9	0,99810	0,99820	0,99830	0,99830	0,99840	0,99840	0,99850	0,99850	0,99860	0,99860
+3,0	0,99865	0,99869	0,99874	0,99878	0,99882	0,99886	0,99889	0,99893	0,99896	0,99900
+3,1	0,99903	0,99906	0,99910	0,99913	0,99915	0,99918	0,99921	0,99924	0,99926	0,99929
+3,2	0,99931	0,99934	0,99936	0,99938	0,99940	0,99942	0,99944	0,99946	0,99948	0,99950
+3,3	0,99952	0,99953	0,99955	0,99957	0,99958	0,99960	0,99961	0,99962	0,99964	0,99965
+3,4	0,99966	0,99967	0,99969	0,99970	0,99971	0,99972	0,99973	0,99974	0,99975	0,99976
+3,5	0,99977	0,99978	0,99978	0,99979	0,99980	0,99981	0,99981	0,99982	0,99983	0,99983

Приложение 2

Критические точки распределения 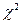с числом степеней свободы 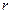на уровне значимости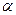

r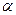
0,99	0,98	0,95	0,90	0,80	0,70	0,50	0,30	0,20	0,10	0,05	0,02	0,01	0,001
	0,000	0,001	0,004	0,016	0,064	0,148	0,455	1,074	1,642	2,710	3,840	5,410	6,640	10,830
	0,020	0,040	0,103	0,211	0,446	0,713	1,386	2,410	3,220	4,600	5,990	7,820	9,210	13,820
	0,115	0,185	0,352	0,584	1,005	1,424	2,370	3,660	4,640	6,250	7,820	9,840	11,340	16,270
	0,297	0,429	0,711	1,064	1,649	2,200	3,360	4,880	5,990	7,780	9,490	11,670	13,280	18,460
	0,554	0,752	1,145	1,610	2,340	3,000	4,350	6,060	7,290	9,240	11,070	13,390	15,090	20,500
	0,872	1,134	1,635	2,200	3,070	3,830	5,350	7,230	8,560	10,640	12,590	15,030	16,810	22,500
	1,239	1,564	2,170	2,830	3,820	4,670	6,350	8,380	9,800	12,020	14,070	16,620	18,480	24,300
	1,646	2,030	2,730	3,490	4,590	5,530	7,340	9,520	11,030	13,360	15,510	18,170	20,100	26,100
	2,090	2,530	3,320	4,170	5,380	6,390	8,340	10,660	12,240	14,680	16,920	19,680	21,700	27,900
	2,560	3,060	3,940	4,860	6,180	7,270	9,340	11,780	13,440	15,990	18,310	21,200	23,200	29,600
	3,050	3,610	4,580	5,580	6,990	8,150	10,340	12,900	14,630	17,280	19,680	22,600	24,700	31,300
	3,570	4,180	5,230	6,300	7,810	9,030	11,340	14,010	15,810	18,550	21,000	24,100	26,200	32,900
	4,110	4,760	5,890	7,040	8,630	9,930	12,340	15,120	16,980	19,810	22,400	25,500	27,700	34,600
	4,660	5,370	6,570	7,790	9,470	10,820	13,340	16,220	18,150	21,100	23,700	26,900	29,100	36,100
	5,230	5,980	7,250	8,550	10,310	11,720	14,340	17,320	19,310	22,300	25,000	28,300	30,600	37,700
	5,810	6,610	7,960	9,310	11,150	12,620	15,340	18,420	20,500	23,500	26,300	29,600	32,000	39,300
	6,410	7,260	8,670	10,080	12,000	13,530	16,340	19,510	21,600	24,800	27,600	31,000	33,400	40,800
	7,020	7,910	9,390	10,860	12,860	14,440	17,340	20,600	22,800	26,000	28,900	32,300	34,800	42,300
	7,630	8,570	10,110	11,650	13,720	15,350	18,340	21,700	23,900	27,200	30,100	33,700	36,200	43,800
	8,260	9,240	10,850	12,440	14,580	16,270	19,340	22,800	25,000	28,400	31,400	35,000	37,600	45,300
	8,900	9,920	11,590	13,240	15,440	17,180	20,300	23,900	26,200	29,600	32,700	36,300	38,900	46,800
	9,540	10,600	12,340	14,040	16,310	18,100	21,300	24,900	27,300	30,800	33,900	37,700	40,300	48,300
	10,200	11,290	13,090	14,850	17,190	19,020	22,300	26,000	28,400	32,000	35,200	39,000	41,600	49,700
	10,860	11,990	13,850	15,660	18,060	19,940	23,300	27,100	29,600	33,200	36,400	40,300	43,000	51,200
	11,520	12,700	14,610	16,470	18,940	20,900	24,300	28,200	30,700	34,400	37,700	41,700	44,300	52,600
	12,200	13,410	15,380	17,290	19,820	21,800	25,300	29,200	31,800	35,600	38,900	42,900	45,600	54,100
	12,880	14,120	16,150	18,110	20,700	22,700	26,300	30,300	32,900	36,700	40,100	44,100	47,000	55,500
	13,560	14,850	16,930	18,940	21,600	23,600	27,300	31,400	34,000	37,900	41,300	45,400	48,300	56,900
	14,260	15,570	17,710	19,770	22,500	24,600	28,300	32,500	35,100	39,100	42,600	46,700	49,600	58,300
	14,950	16,310	18,490	20,600	23,400	25,500	29,300	33,500	36,200	40,300	43,800	48,000	50,900	59,700

Приложение 3

Критические точки 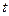-распределения Стьюдента

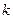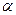0,10	0,05	0,025	0,01	0,005
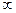	3,078 1,886 1,638 1,533 1,476   1,440 1,415 1,397 1,383 1,372   1,363 1,356 1,350 1,345 1,341   1,337 1,333 1,330 1,328 1,325   1,33 1,321 1,319 1,318 1,316   1,315 1,314 1,313 1,311 1,310   1,303 1,296 1,289 1,282	6,314 2,920 2,353 2,132 2,015   1,943 1,895 1,860 1,833 1,812   1,796 1,782 1,771 1,761 1,753   1,746 1,740 1,734 1,729 1,425   1,721 1,717 1,714 1,711 1,708   1,706 1,703 1,701 1,699 1,697   1,684 1,671 1,658 1,645	12,706 4,303 3,182 2,776 2,571   2,448 2,365 2,306 2,262 2,228   2,201 2,179 2,160 2,145 2,131   2,120 2,110 2,101 2,093 2,086   2,080 2,074 2,069 2,064 2,060   2,056 2,052 2,048 2,045 2,042   2,021 2,000 1,980 1,960	31,821 6,965 4,541 3,747 3,365   3,143 2,998 2,896 2,821 2,764   2,718 2,681 2,650 2,624 2,602   2,583 2,567 2,552 2,239 2,528   2,518 2,508 2,500 2,492 2,485   2,479 2,473 2,467 2,462 2,457   2,423 2,390 2,358 2,326	63,657 9,925 5,841 4,604 4,032   3,707 3,499 3,355 3,250 3,169   1,306 3,055 3,012 2,977 2,947   2,921 2,898 2,878 2,861 2,845   2,831 2,819 2,807 2,797 2,787   2,779 2,771 2,763 2,756 2,750   2,704 2,660 2,576 2,576

Приложение 4