Правила проверки гипотез

Можно проверять гипотезу на основе любой статистики, имеющей любое вероятностное распределение. Можно указать основные случаи: выборочная статистика подчиняются либо нормальному распределению, либо распределению Стьюдента, либо F-распределению, либо 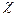²-распределению.

Проверка на основе нормального распределения используется для проверки среднего значения выборки как оценки генеральной средней. Критерий применяется при любом размере выборочной совокупности, когда дисперсия генеральной совокупности известна.

Распределение Стьюдента(t-критерий) используется для проверки гипотезы о среднем значении при любом объеме выборки при неизвестной генеральной дисперсии. При больших выборках это распределение приближается к нормальному распределению.

F-критерий используется для сравнения генеральных дисперсий. Размер выборки может быть любым при условии, что выборка взята из генеральной совокупности.

Критерий 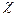² – непараметрический, т.е. значения выборочной статистики не требуются. Этот критерий основан на частоте появления значений случайных переменных. Используется для проверки гипотезы связи между переменными или о согласии наблюдаемого распределения с некоторым стандартным распределением.

1. Сравнение двух средних генеральных совокупностей, дисперсии которых известны.

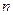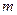Рассмотрим достаточно большие независимые выборки. Пусть и – объемы больших ( 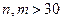) независимых выборок, по которым найдены выборочные средние 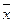, 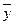Генеральные дисперсии 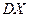, 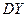известны.

Гипотеза :

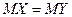
Гипотеза :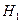

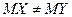
Вычислим наблюдаемое значение критерия

.

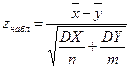По таблице (см. Приложение 1), зная значение функции Лапласа 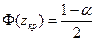, найдем критическую точку .

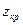Если 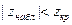- нет оснований отвергать гипотезу _, в противном случае – нулевую гипотезу отвергаем.

Другой вариант формулировки гипотез:

Гипотеза :

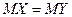
Гипотеза :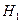

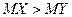
Критическую точку 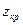находим, зная значение функции Лапласа .

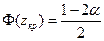Если 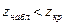– нет оснований отвергать , если неравенство другого знака, то отвергаем.

Гипотеза :

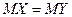
Гипотеза :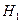

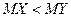
Находим значение 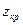так же, как в предыдущем пункте.

Если 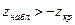– нет оснований отвергать , если неравенство другого знака – отвергаем.

Сравнение средних двух совокупностей имеет важное практическое значение. На практике часто встречаются случаи, когда средний результат одной серии экспериментов отличается от среднего результата другой серии. При этом возникает вопрос, можно ли объяснить обнаруженное расхождение средних неизбежными случайными ошибками эксперимента или оно вызвано некоторыми закономерностями. В промышленности задача сравнения средних часто возникает при выборочном контроле качества изделий, изготовленных на разных установках.

Пример 1. По двум независимым выборкам, объемы которых 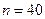и , и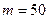звлеченным из нормальных генеральных совокупностей, найдены выборочные средние: 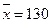и 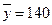. Генеральные дисперсии известны: 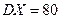, 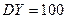. Требуется при уровне значимости 0,01 проверить нулевую гипотезу : 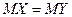при конкурирующей гипотезе : .

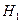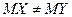Решение. Найдем наблюдаемое значение критерия:

.

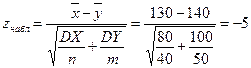По условию, конкурирующая гипотеза имеет вид , 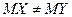поэтому критическая область – двусторонняя.

Найдем правую критическую точку из равенства

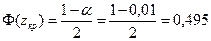
По таблице функции Лапласа (см. Приложение 1) находим .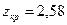

Т.к. 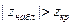_, то в соответствии с теорией нулевую гипотезу отвергаем. Другими словами, выборочные средние различаются значимо.

2. Сравнение двух средних нормальных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки).

Пусть 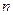и 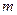объемы малых независимых выборок ( 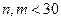), по которым найдены 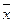, 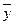и исправленные выборочные дисперсии 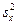, 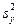. Генеральные дисперсии хоть и неизвестны, но предполагаются одинаковыми. Уровень значимости задан.

Гипотеза :

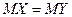
Гипотеза :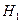

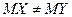
Для проверки нулевой гипотезы в этом случае можно использовать критерий Стьюдента сравнения средних. Величину критерия находим по формуле:

.

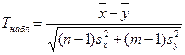Доказано, что величина 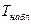при справедливости нулевой гипотезы имеет 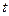-распределение Стьюдента с 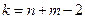степенями свободы (см. Приложение 3).

По таблице находим .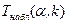

Сравниваем 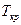и 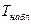_. Если 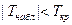, то принимаем . Если 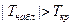, то гипотеза отвергается и принимается 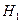и различие достоверно.

Другой вариант формулировки гипотез:

Гипотеза :

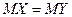
Гипотеза :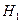

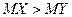
По таблице по уровню 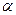, по 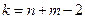находим 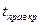_. Если 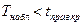, то нет оснований отвергать . В противном случае – отвергаем.

Гипотеза :

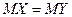
Гипотеза :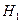

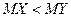
По таблице находим 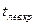. Если 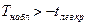– нет оснований отвергнуть , в противном случае – отвергаем.

1. Проверка гипотез для дисперсий.

Пусть генеральные совокупности и распределены нормально. По независимым выборкам объемов 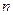и , и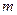звлеченным из этих совокупностей, найдены исправленные выборочные дисперсии 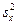, 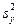. Требуется сравнить эти дисперсии. При заданном уровне значимости 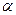надо проверить нулевую гипотезу о равенстве генеральных дисперсий нормальных совокупностей.

Гипотеза :

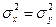
Гипотеза :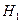

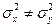
В качестве критерия проверки нулевой гипотезы о равенстве генеральных дисперсий используем случайную величину 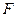, равную отношению большей исправленной выборочной дисперсии к меньшей .

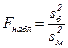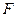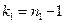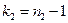Величина , при условии справедливости нулевой гипотезы, имеет распределение Фишера - Снедекора со степенями свободы и , где 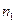- объем выборки, по которой вычислена большая выборочная дисперсия.

Из таблиц (см. Приложение 4) находим 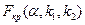. Сравниваем 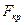и 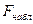. Если 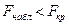, то принимаем нулевую гипотезу, генеральные дисперсии различаются незначимо.

Пример 2. По двум независимым малым выборкам, объемы которых 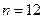и , и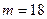звлеченным из нормальных генеральных совокупностей и 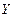, найдены выборочные средние: 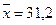, 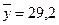и исправленные дисперсии 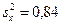, 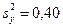. Требуется при уровне значимости 0,05 проверить нулевую гипотезу : 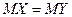при конкурирующей гипотезе : .

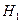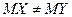Решение. Исправленные дисперсии различны, поэтому проверим предварительно гипотезу о равенстве генеральных дисперсий, используя критерий Фишера - Снедекора.

Найдем отношение большей дисперсии к меньшей: 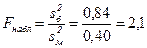. Дисперсия 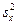значительно больше дисперсии 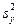, поэтому в качестве конкурирующей гипотезы примем гипотезу 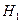: 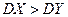. В этом случае критическая область – правосторонняя. По таблице приложений по уровню значимости 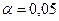и числам степеней свободы 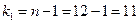и 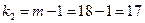находим критическую точку .

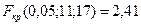Т.к. 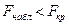– нет оснований отвергнуть нулевую гипотезу о равенстве двух генеральных дисперсий.

Предположение о равенстве генеральных дисперсий выполняется, поэтому сравним средние.

Вычислим наблюдаемое значение критерия Стьюдента .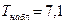

По условию, конкурирующая гипотеза имеет вид 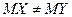, поэтому критическая область – двусторонняя. По уровню значимости 0,05 и числу степеней свободы 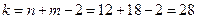находим по таблице Приложения 3 критическую точку .

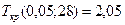Т.к. 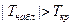– нулевую гипотезу о равенстве средних отвергаем. Другими словами, выборочные средние различаются значимо.

1. Проверка гипотез о законах распределения.

Во многих практических задачах закон распределения случайных величин заранее неизвестен, и надо выбрать модель, согласующуюся с результатами наблюдений.

Выдвигают нулевую гипотезу : неизвестная функция распределения 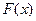есть функция распределения некоторого теоретического закона 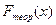, например, нормального, или экспоненциального, или биномиального. Это определяется сущностью изучаемого явления, а также результатами предварительной обработки наблюдений: формой графика распределения, соотношениями между выборочными данными.

Выдвигается альтернативная гипотеза, что данная генеральная совокупность не распределена по закону .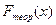

Задается уровень значимости, например .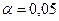

Если хотим проверить, согласуются ли эмпирические данные с нашим гипотетическим предположением относительно теоретической функции распределения или нет, то используем критерий согласия.

Критерии согласия строятся на основе выбора некоторой статистики, характеризующей отклонение эмпирических данных от данных, соответствующих гипотезе . Одним из наиболее известных таких критериев является критерий 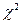- Пирсона.

Критерий 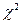- Пирсона

Критерий 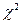применяют для проверки гипотезы о том, что случайная величина подчинена закону распределения 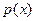, по выборке 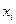, 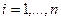. По выборке 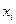строят функцию распределения случайной величины .

Для этого область изменения значений случайной величины разбивают на интервалы 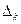, , 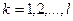и определяют частоту попадания значений случайной величины в каждый интервал 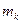, а также теоретическую вероятность 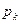. Затем вычисляют значение случайной величины

,

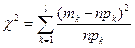которая распределена по закону 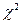с 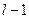степенями свободы.

При помощи таблиц находят границу критической области 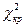при уровне значимости 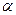. Если 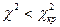, то принимается решение о справедливости основной гипотезы, в противном случае принимается решение о справедливости альтернативы.