ГЛАВА 6. Специфика формирования математических понятий. Методика работы с правилами и алгоритмами. Обучение решению задач. ИЗУЧЕНИЕ теорем

6.1. Специфика формирования математических понятий у особенных учащихся.

В психологии понятием называют форму мышления, в которой отражаются общие и существенные свойства явлений, при этом понятие является как результатом, так и средством мышления. Любое понятие характеризуется содержанием и объемом. Объем понятия раскрывается, как правило, с помощью операции классификации. Содержание понятия раскрывается через определение. В речи понятие фиксируется с помощью слова или словосочетания, называемого именем или термином понятия. В математике понятие часто обозначается не только термином, но и символом.

Методика изучения того или иного понятия зависит от ряда факторов: насколько сложным является понятие; в какой мере оно подготовлено жизненным опытом учащихся; в каком классе изучается понятие; знакомятся ли учащиеся с понятием впервые или имела место пропедевтика понятия; каковы индивидуально-типологические особенности учащихся и др. Образование понятий связано с установлением общих свойств у предметов, выделением существенных признаков, соединением их в определенное единство. В формировании понятий большую роль играют такие операции мышления, как анализ, синтез, сравнение, абстрагирование, обобщение и др. Однако именно эти мыслительные операции недостаточно развиты у отстающих в учении и имеющих отклонения в развитии школьников. Это следует учитывать при изучении понятий особенными учащимися. Кроме того, особенности детей данной категории требуют преподнесения материала небольшими дозами, с более постепенным, чем обычно усложнением, более дробно.

Организуемый учителем процесс усвоения понятия может быть представлен в виде следующей последовательности этапов [5; 10; 20]: подготовка к введению нового понятия; мотивация введения понятия; организация восприятия и понимания; применение в стандартных и нестандартных ситуациях. В методике обучения математике выделяются два метода введения понятий (К.Ф. Лебединцев): конкретно-индуктивный и абстрактно-дедуктивный. Отстающим в учении школьникам предпочтителен конкретно-индуктивный метод. Абстрактно-дедуктивный метод может применяться в тех случаях, когда введение понятия хорошо подготовлено предшествующим обучением.

Система упражнений на усвоение понятия призвана: способствовать мотивации введения понятия; выявлять и способствовать усвоению существенных свойств понятия; способствовать усвоению терминологии, символики, пониманию смысла каждого слова в определении, запоминанию определения, овладению объемом понятия; раскрывать взаимосвязь понятия с другими понятиями; обучать применению понятия и логическим операциям с понятиями.

При формировании понятий у особенных учащихся следует максимально учитывать исследования психологии [6; 13; 17], коррекционной педагогики [18; 33], методики обучения математике [5; 7; 8; 10; 16; 20; 27; 29]. Обратимся, например, к теории поэтапного формирования умственных действий (П.Я. Гальперин и др.). Эта теория предусматривает постепенный перевод внешних материализованных действий во внутренние, умственные, действия. Этот перевод совершается в пять этапов. На первом этапе учащимся разъясняют цель введения нового понятия, указывают, на что надо ориентироваться при формулировании определения понятия. Например, при введении понятия параллелограмма такую ориентировку естественно дать с помощью чертежа. При этом учитель сообщает, что нарисованная фигура – параллелограмм и он будет определен как четырехугольник, который обладает некоторыми свойствами. Какими именно? В итоге формулируется определение. На втором этапе учащиеся сами формулируют определение, исходя из рисунка (вначале выполняется рисунок, затем проговаривается определение). На третьем этапе учащиеся формулируют определение вслух, без опоры на рисунок. На четвертом этапе определение проговаривается в форме внешней речи про себя, на пятом – в форме внутренней речи. Во многих случаях эти этапы протекают почти слитно, не занимают много времени, выполняются с помощью традиционных методических приемов. Естественно, что учитель мотивирует изучение нового понятия (первый этап), приводит материальные объекты, с помощью которых формулируется определение. Полезно, когда ученик формулирует определение, одновременно показывая то, о чем он говорит, на рисунке (второй этап). Проговаривание определения вслух, без опоры на рисунок, модель и т.д. (третий этап), является важным для формирования у учащихся правильной математической речи. При подготовке учащимися домашних заданий полезно заучивать материал, если не вслух, то с помощью внешней речи про себя (четвертый этап). Этот этап важен с точки зрения активного запоминания учебного материала. На третьем и четвертом этапах необходимо постоянно напоминать учащимся, чтобы они мысленно представляли себе тот объект, который ими определяется. В этом случае третий и четвертый этапы будут способствовать развитию пространственных представлений и воображения учащихся.

Важно помнить, что процесс формирования понятий не оканчивается их введением. Он продолжается при использовании этих понятий для определения других понятий, формулировании теорем, проведении доказательств, решении задач.

Покажем, в качестве примера, каким образом может быть организовано усвоение особенными учащимися понятия «десятичная дробь». Десятичные дроби чаще, чем обыкновенные, используются в жизни и имеют большое практическое значение. С десятичными дробями учащиеся будут встречаться и на производстве, и в быту.

С десятичными дробями учащиеся классов КРО знакомятся после изучения целых чисел и обыкновенных дробей. Успех усвоения десятичных дробей во многом зависит от знания учащимися нумерации целых чисел, свойств десятичной системы счисления и десятичного соотношения мер метрической системы (длины, стоимости, массы). Все эти знания необходимо воспроизвести в памяти учащихся перед тем, как переходить к изучению десятичных дробей.

Учитывая конкретность мышления особенных уча­щихся, понятие о десятичной дроби целесообразнее всего сформи­ровать, используя знания учащихся о соотношениях метрической системы единиц измерения длины. В качестве наглядного пособия используется метр, разделенный на дециметры, сантиметры и мил­лиметры. Учащиеся вспоминают, что в 1 м содержится 10 дм, 100 см и 1000 мм. Теперь можно установить, какую часть метра составляет 1 дм, 1 см и 1 мм, и записать: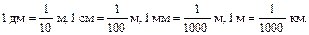

Аналогично повторяется соотношение единиц измерения стоимости и массы и устанавливается, что 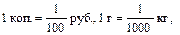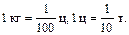Далее учащимся предлагается упражнение: выразить в метрах 2 м 3 дм 6 см 7 мм. Задание выполняется с подробными пояснениями всех преобразований:

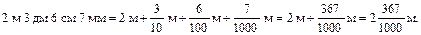Далее учитель просит учащихся записать подряд без наименования все дроби, которые получили, с тем, чтобы обратить внимание на знаменатели этих дробей. Учащиеся на основе наблюдений уста­навливают, что у всех дробей знаменатели 10, 100, 1000, т. е. единица с одним или несколькими нулями. Учитель формулирует вывод: дробь, у которой знаменатель – единица с одним или несколькими нулями, называется десятичной дробью.

Далее учащимся предлагается записать под диктовку несколько дробей 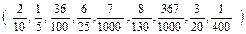и объяснить, как получилась каждая из дробей, а затем назвать только десятичные дроби. При этом следует подчеркнуть общность в полу­чении обыкновенных и десятичных дробей: при получении десятич­ных дробей целое (единица) делится на 10, 100, 1000 и т. д. равных частей, т. е. на столько равных частей, сколько единиц в знаменателе. Например, чтобы получить дробь 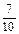,надо взять отрезок (единицу) и разделить его на 10 равных частей, а затем взять 7 таких частей.

Десятичная дробь может получаться и при измерении. Напри­мер, при измерении ленты длина ее оказалась равной 8 дм, или 80 см, а это составляет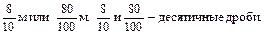

Письменная нумерация десятичных дробей тесно связана с нумерацией целых чисел, со свойствами десятичной системы счисления. Поэтому, прежде чем учиться записи десятичных дробей, следует вспомнить нумерацию целых чисел, повторить поместное значение цифры в числе.

На доске вычерчивается таблица разрядов числа 1234, в которой целые разряды отделены от дробных жирной линией.

Единицы тысяч	Сотни	Десятки	Единицы	Десятые доли	Сотые доли	Тысячные доли

В числе 1234: цифра 4, стоящая на первом месте справа, означает 4 единицы; цифра 3, стоящая на втором месте справа, означает 3 десятка; цифра 2, стоящая на третьем месте справа, означает 2 сотни; цифра 1, стоящая на 4 месте справа, означает 1 тысячу. Итак, каждая цифра, стоящая левее данной, обозначает единицы, которые в 10 раз больше данной. Выделяется главное свойство соседних разрядов: единицы разряда справа в 10 раз меньше единиц разряда, находящегося от него слева. Если, например, разрядную единицу переместить слева направо, то она уменьшится в 10 раз. Справа от разряда единиц, за границей целых чисел, находится разряд, в 10 раз меньший, то есть десятые доли, далее сотые, тысячные и т.д. Таким образом, место десятичных долей в таблице классов и разрядов определено.

Следует спросить учащихся, что будет означать какая-либо цифра (например, 1) если ее записать в таблицу на месте одного из разрядов, следующих за разрядом единиц. (Если справа от числа 1234 написать цифру 1, то она будет обозначать число, в 10 раз меньшее, чем 1 единица. Это одна десятая доля единицы. Если справа записать еще 1 единицу, то она будет меньше десятой доли в 10 раз и единицы в 100 раз. Это одна сотая доля единицы. Записав справа еще одну единицу, получим тысячную долю единицы).

Единицы тысяч	Сотни	Десятки	Единицы	Десятые доли	Сотые доли	Тысячные доли

Затем можно рассмотреть результаты измерения длин отрезков, записанные в следующем виде:

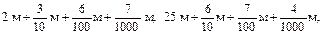
и предложить учащимся вписать эти числа в таблицу разрядов. Потом, наоборот, записав какую-либо десятичную дробь в таблицу разрядов, предложить выполнить обратную задачу. После выполнения таких упражнений учащимся сообщается, что вместо черты, отделяющей дробные разряды от целых, принято ставить запятую. В результате справа от таблицы появляется новый вид записи одной и той же величины. Общий вид записи на доске указан в таблице.

	Сотни	Десятки	Единицы	Десятые доли	Сотые доли	Тысячные доли
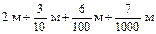							2,367
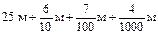							25,674

Затем выполняют такое же упражнение только без таблицы. Например, 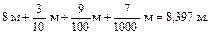Основная цель этих упражнений – добиться ясного понимания учащимися роли запятой в новой записи десятичной дроби и прочного знания разрядов, стоящих справа от запятой. Поэтому каждый новый вид упражнений рекомендуется выполнять с помощью таблицы. При выполнении таких заданий числа читаются только поразрядно. Например, 3,137 читаем: 3 целых 1 десятая 3 сотых 7 тысячных.

Когда учащиеся научатся читать десятичные дроби поразрядно, переходим к более рациональному чтению всей дробной части в одних долях, самых малых. Для этого предлагаем упражнения с иной последовательностью записи. Например,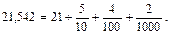

Раздробив десятые и сотые доли в тысячные, получаем 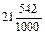и читаем: 21 целая 542 тысячных.

Далее идет обучение записи обыкновенных дробей со знаменателями 10, 100, 1000 и т.д. в виде десятичных. Здесь также применяется таблица записи разрядов. Наибольшую трудность для особенных учащихся представляет запись десятичных дробей (так же как и целых чисел) с отсутствующими разрядными долями, например: 20,07; 20,07; 7,109. Записанная ниже таблица наглядно демонстрирует необходимость появления нулей в записи десятичной дроби.

	Десятки	Единицы	Десятые доли	Сотые доли	Тысячные доли
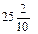						25,2
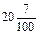						20,07
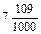						7,109

Эти дроби предлагаются для записи только тогда, когда учащиеся хорошо усвоят запись дробей с наличием всех разрядных долей, могут объяснить, как называется каждая разрядная доля, на каком месте справа от запятой она стоит, поймут, что каждая последующая доля в 10 раз меньше предыдущей (если имеет одно и тоже число долей). Например, 5 сотых в 10 раз меньше, чем 5 десятых, а 5 тысячных в 10 раз меньше, чем 5 сотых.

По следующей таблице учащимся можно показать, что если постепенно увеличивать, например, число сотых долей, то когда их наберется десять или больше, заполнится предыдущий разряд и нули на месте этих разрядов исчезнут.

	Десятки	Единицы	Десятые доли	Сотые доли
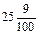					25,09
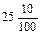					25,10 (или 25,1)
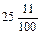					25,11

При знакомстве с письменной нумерацией десятичных дробей необходимо обратить внимание учащихся на то, что после запятой в десятичной дроби должно стоять столько знаков, сколько нулей в знаменателе дроби. Например, надо записать дробь семь целых восемь сотых. Знаменатель дроби 100, т. е. имеет два нуля. Сле­довательно, после запятой должно быть два знака, произносится же только один знак (цифра 8), значит, сразу после запятой надо написать нуль: 7,08. На эту особенность, которую мы используем при записи десятичных дробей, следует обратить внимание учащихся и при их чтении.

Если в дроби нет ни одной целой, то вместо нее пишется нуль. Например, обыкновенную дробь 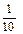можно записать без знаменателя 0,1. Читается эта дробь так: нуль целых одна десятая. Следует сравнить чтение и запись обыкновенных и десятичных дробей.

Обыкновенные дроби	Десятичные дроби
запись	чтение	запись	чтение
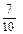	семь десятых	0,7	нуль целых семь десятых
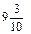	девять целых три десятых	9,3	девять целых три десятых

При чтении десятичных дробей учащиеся школы VII вида очень часто затрудняются в назывании знаменателя десятичной дроби. Они либо его не называют (например, дробь 0,375 читают так: нуль целых триста семьдесят пять), либо вместо тысячных говорят десятые, сотые и др. Чтобы снять эту трудность при чтении десятичных дробей, следует показать учащимся, что если после запятой стоит один знак (цифра), то знаменатель этой дроби – единица с одним нулем, т. е. десять, и нужно добавлять слово «десятых» (соответ­ственно указать на дроби с сотыми и тысячными долями).

Объяснить запись десятичной дроби можно также, используя числа, полученные от измерения. Сначала следует взять числа с соотношением между крупными и мелкими мерами, равными 10, затем 100, наконец 1000. Например, 1 см 5 мм можно записать с одним наименованием, рассуждая следующим образом: в числе 1 см 5 мм есть 1 целый сантиметр и 5 мм, которые составляют 5 десятых сантиметра, т.к. 1 мм равен одной десятой сантиметра. Это число можно записать десятичной дробью: 1,5 см, т. е. написать целое число сантиметров (1), поставить запятую, а 5 десятых сантиметра, т. е. десятые доли сантиметра пишутся после целых (после запятой). Знаменатель 10 не пишется, но читается: одна целая пять десятых сантиметра.

После записи чисел с соотношением между мерами измерения, равным 10, аналогично объяснить запись чисел, полу­ченных от измерения с соотношением мер, равным 100 (затем 1000) и запись этих чисел десятичной дробью. Например, 3 р. 25 к.=3,25 р. (в одном рубле 100 копеек, значит 25 к. – это 25 сотых частей рубля: записывается целое число 3, ставится запятая, а после нее пишется 25 сотых, т. е. 3,25 р., знаменатель не пишется, но читается. 10 р. 08 к.=10,08 р., 1 ц 05 кг = 1,05 ц и т.д. Аналогично записываются десятичной дробью именованные числа с соотношением мер, равным 1000. Например, 1 кг 375 г=1,375 кг, 5 кг 085 г=5,085 кг, 7 т 004 кг=7,004 т.

Учащиеся должны понять единый принцип – десятичный, которому подчиняются соотношения между единицами измерения в метрической системе мер и между разрядными единицами в таблице разрядов.