Свойства и признаки равнобедренной трапеции

• В равнобедренной трапеции, прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции.
• Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований
• В равнобедренной трапеции углы при любом основании равны.
• В равнобедренной трапеции длины диагоналей равны.

Площадь

Здесь приведены формулы, свойственные именно трапеции. См. также формулы для площади произвольных четырёхугольников.

• В случае, есл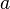и и 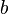— основания и 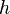— высота, формула площади:

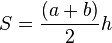
• В случае, если 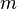— средняя линия и 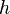— высота, формула площади:

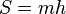
Смежные и вертикальные углы. Перпендикулярные прямые

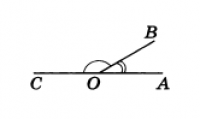
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.

Сумма смежных углов равна 180°

Рис.1

Теорема 1.Сумма смежных углов равна 180°.

Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180°.

Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.

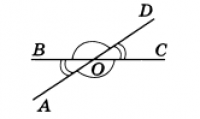
Вертикальные углы равны

Рис.2

Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).

Теорема 2.Вертикальные углы равны.

Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1 ∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.

Отсюда заключаем, что ∠ АОВ = ∠ COD.

Следствие 1.Угол, смежный с прямым углом, есть прямой угол.

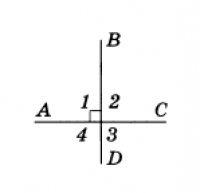
Рис.3

Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.

Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.

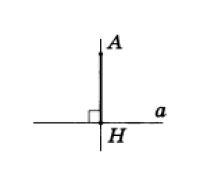
АН — перпендикуляр к прямой

Рис.4

Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.

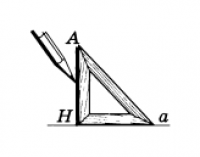
Чертежный угольник

Рис.5

Справедлива следующая теорема.