Модель CAPM, рыночная модель

Модель САРМ

Модель САРМ (предложена в 1964-1966 годах независимо друг от друга У. Шарпом (William. Sharp), Дж. Линтнером (John Lintner) и Я Моссином (Jan Mossin)) вводит понятие рыночного портфеля общего для всех инвесторов на место касательного портфеля отдельного инвестора. Из этой модели вытекает рыночная модель, которая ранее была введена другим образом как одноиндексная модель Шарпа.

Альтернативная модель оценки финансовых активов – теория арбитражного ценообразования, разработана Стефаном Россом (Stephen Ross)[17]

Предпосылки модели САРМ:

Определение:

Портфель называется рыночным (market) портфелем, если доля средств, вложенных в каждую ценную бумагу портфеля, равна доле средств, вложенных в эту бумагу на рынке в целом.

Оказывается, что в рамках предположений модели САРМ (Capital Asset Pricing Model) касательный портфель, имеющий отношение котдельномуинвестору,являетсярыночным портфелем.

Доказательство.

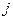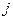Пусть доля произвольной ценной бумаги в касательном портфеле инвестора равна , то есть инвестор вложил денег в свой портфель ценных бумаг, из которых денег он вложил в бумагу . Ранее мы доказали, что, согласно модели Тобина, структура оптимального рискового портфеля для всех инвесторов одинакова.

Логика доказательства такова: сначала доказывается, что луч, проведенный из точки с параметрами безрисковой бумаги по касательной к допустимому (еще точнее, эффективному) множеству рисковых портфелей является допустимым множеством для портфелей, совмещающих рисковые и безрисковые бумаги (правда, в точке касания все бумаги только рисковые). Учитывая, что допустимый портфель рисковых бумаг является выпуклым, касательная является единственной.

Далее, учитывая, что точка с параметрами безрисковой бумаги и точка касания касательной к допустимому множеству рисковых бумаг являются допустимыми точками, мы делаем вывод, что и точки расположенные на касательной (луче) являются также допустимыми точками.

Это следует из утверждения, что в любом случае допустимое множество портфелей должно быть выпуклым. То есть допустимыми должны быть и все точки, расположенные на отрезке между допустимыми точками.

Доказывается это методом от обратного. Если предположить, что две крайние точки отрезка являются допустимыми точками, а внутренние точки – недопустимыми, возникает противоречие. Мы можем брать в качестве допустимых портфели бумаг в соответствии с параметрами крайних точек отрезка, но почему-то не можем составить смесь из крайних портфелей. Если же предположить возможность не только покупки безрисковых бумаг, но и их выпуска (то есть займа), допустимым становится весь луч, проведенный из точки безрискового портфеля по касательной к допустимому множеству рисковых портфелей.

Но мало, что точки на касательной (луче) располагаются допустимые портфели. Доказывается, что эти точки образуют эффективное множество (то есть такое допустимое множество портфелей, лучше которых инвестор не может выбрать) и, таким образом, точка касания луча является единственной эффективной точкой рисковых портфелей для всех инвесторов.

Повторяем, единственность эффективной точки следует из выпуклости допустимого и эффективного множества портфелей.

Доказывается, это также от противного. Достаточно предположить, что касательная к допустимому рисковому портфелю не является эффективным множеством. Тогда мы должны предположить существование эффективных точек левее нашего луча и, таким образом, существование допустимого рискового портфеля левее всего допустимого множества рисковых портфелей. А это невозможно.

Напомним, что по предположениям всех моделей, начиная с модели Марковица, все инвесторы имеют одинаковые представления об ожидаемых доходностях и рисках каждой ценной бумаги, поэтому допустимые множества для всех инвесторов одинаковы. Доходность безрисковой ценной бумаги также едина для всех инвесторов. Следовательно, касательный портфель для всех инвесторов один. Учитывая, что доходность и риск касательного портфеля определяются его структурой, структура оптимального рискового портфеля для всех инвесторов одна

Если структура рискового портфеля для всех инвесторов одинакова, и каждый инвестор вложил в бумагу долю своих средств, то все инвесторы (от 1 до 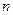) вместе вложили в денег в бумагу . В этом случае доля средств, вложенных в бумагу всем рынком (всеми инвесторами вместе), составляет .

Мы доказали, таким образом, что доля средств, вложенная в бумагу каждым инвестором равна доле средств, вложенных в бумагу всеми инвесторами, то есть, равна доле бумаги на рынке. Мы доказали, что касательный портфель является и рыночным портфелем.

Предполагается также, что на совершенном (эффективном) рынке отклонения от установленного правила должны компенсироваться. Если инвесторы не приобретают, например, ценную бумагу А в рыночном объеме, то есть предложение бумаги А больше спроса на нее, то цена этой бумаги должна снизиться и, соответственно, доходность увеличиться. В связи с увеличением доходности бумаги А, спрос на нее должен вырасти.

В модели предполагается, что уменьшение цены финансового актива в начале холдингового периода увеличивает его доходность в течение холдингового периода. Заметим, что доходность финансового актива в конце холдингового периода вычисляется следующим образом:

, где

- доходность финансового актива (акции, облигации) в конце холдингового периода;

, - цены финансового актива в начале и конце холдингового периода;

- выплаты по финансовому активу (дивиденды по акциям, проценты по облигациям) в течение холдингового периода.

Определение.

Рыночной линией капитала (Capital Market Line, CML) называется эффективное множество портфелей.

По ранее доказанному эффективное множество портфелей при наличии безрискового актива находится на луче, идущем от точки F через точку T (точку касательного портфеля).

Если точка T в соответствии предположениями модели CAPM отражает рыночный портфель, то касательная является рыночной линией капитала.

Теорема 1. Касательная к рыночному портфелю (точка рыночного портфеля – это есть одновременно и точка касательного портфеля) является рыночной линией капитала, то есть эффективным множеством портфелей

Доказательство.

Теорема доказывается от противного. Предположим, что касательная к кривой в точке 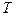- это линия , которая не совпадает с линией CML. Точнее, положим, что линия имеет угол больше, чем линия CML. Тогда и точки кривой АТ (показана прерывистой линией), расположенные правее Т, лежат выше линии CML.

Точка А (произвольная ценная бумага) и точка Т (рыночный портфель) заданы. Портфель П может не существовать. В этом случае точки кривой АТ, расположенные правее точки Т являются решением, содержащим отрицательную долю бумаг А в рыночном портфеле Т.

Последнее означает, что все инвесторы, формируя рыночный портфель (а он является оптимальным для портфеля рисковых ценных бумаг), должны стремиться продать бумагу А. Следовательно, рынок не является сбалансированным, не находится в состоянии равновесия. Это противоречит одной из предпосылок нашей модели, что для любого допустимого портфеля спрос на бумаги равен предложению бумаг.

Если линия L имеет угол наклона меньше, чем линия СМL, то возникает ситуация, когда допустимые портфели около точки Т лежат выше линии CML, эффективного множества портфелей, что невозможно. Таким образом, касательная, проведенная к кривой АТ должна совпадать с рыночной линией капитала CML, чтобы допустимые рисковые портфели находились правее и ниже точки Т.