Приведем самые общие допущения портфельного анализа, касающиеся индивидуального инвестора, определяющие степень знания инвестора о рынке и некоторые свойства рынка

1. Не существует операционных издержек или налогов, связанных с покупкой или продажей ценных бумаг.

2. Все инвестиционные решения принимаются только на один период времени.

3. Инвесторы могут прогнозировать ожидаемую величину доходности каждой ценной бумаги.

4. Инвесторы могут прогнозировать среднеквадратическое отклонение распределения вероятностей доходности каждой ценной бумаги. Когда каждая ценная бумага рассматривается отдельно, они используют эту цифру так, как будто она является полным измерением риска. Они могут предсказать корреляцию между доходностями для любой пары ценных бумаг.

5. Привлекательность ценной бумаги или портфеля полностью определяется тремя переменными: а) ожидаемой доходностью; б) индивидуальным риском, измеренным среднеквадратическим отклонением (или дисперсией) доходности и корреляцией данных с доходностью других ценных бумаг или их портфелем.

По поводу допущений Бромвич М. разумно замечает[9] : В теории инвестиционного портфеля считается, что инвесторы не осуществляют такие расчеты для получения ожидаемого дохода от ценных бумаг. Скорее в теории предполагается, что инвесторы действуют таким образом, как будто их «наилучшее мнение» относительно доходности любых ценных бумаг эквивалентно теоретической ожидаемой доходности. Это очень важное замечание, которое может быть отнесено, вообще, к взаимосвязи экономической теории и практики.

Логика дальнейшего изложения модели Марковица такова (конкретные выкладки осуществляются для портфеля из двух ценных бумаг):

1. Вводится и исследуется функция полезности инвестора от доходности и риска ценных бумаг.

2. На основе функции полезности строятся кривые безразличия доходности и риска для каждого уровня полезности.

3. Выводятся формулы доходности и риска портфеля ценных бумаг в зависимости от структуры портфеля и известных доходности и риске каждой ценной бумаги.

4. Строится допустимое и эффективное множества доходов и рисков портфелей ценных бумаг различной структуры при известных доходах и рисках каждой ценной бумаги.

5. На эффективном множестве находится точка касания кривых безразличия и эффективного множества – оптимальная точка для каждого инвестора.

B. Анализ функции полезности инвесторов

У инвесторов могут быть различные предпочтения относительно доходности и риска.

Инвестор может избегать риска. Тогда увеличение риска будет требовать все увеличивающейся доходности.

Инвестор может интересоваться только определенным уровнем риска, который принимает при любом уровне доходности. Тогда увеличение риска не будет требовать увеличения доходности.

Инвестор может интересоваться только определенным уровнем доходности, который принимает при любом уровне риска. Тогда увеличение доходности не будет сопровождаться обязательным увеличением риска.

И инвестор может в той или иной степени избегать риска.

Представим функцию полезности для инвестора, который, скорее будет избегать азартной игры, во всяком случае, будет ждать платы за самое участие в игре.

Предположим, что в игре заключена вероятность выигрыша 1 млн. рублей и проигрыша той же суммы с вероятностями соответственно 0.5; 0.5. Тем не менее, субъективная оценка вероятного выигрыша и потери у нашего игрока различна. Вред от потери 1 млн. рублей игрок оценивает выше столь же вероятного выигрыша 1 млн. рублей. И хотя математическое ожидание данной игры равно 0, наш игрок согласится на игру лишь с учетом выплаты известной премии. Ее величина определяется точкой Е, которая делит пополам отрезок между полезностью выигрыша 1 млн. рублей и вредом от проигрыша.

Рис 1. Поведение инвестора не склонного к риску

Теперь покажем функцию полезности для инвестора, который, скорее всего, будет участвовать в азартной игре. Теперь наш игрок является оптимистом и оценивает вероятный выигрыш выше столь же вероятной потери. Он готов даже заплатить за участие в такой игре сумму, определяемую точкой F.[10] Величина платы так же определяется точкой, делящей пополам отрезок от точки полезности выигрыша до точки вреда проигрыша.

Рис 2. Поведение азартного инвестора

В теории инвестиционного портфеля предполагается, что игрок избегает риска, во всяком случае, ожидает за дополнительный риск дополнительный доход.

Если выражаться точнее, то в теории инвестиционного портфеля принимают разумные допущения относительно предпочтений между риском и доходностью ценной бумаги:

1. Предполагается, что при прочих равных условиях инвесторы предпочитают большую доходность меньшей.

2. Инвесторы предпочитают меньший риск большему, т. е. предполагается, что инвесторы избегают риска.

Отсюда правило:

Инвестор будет максимизировать свой ожидаемый доход при данной степени риска или минимизировать свой риск при данном уровне дохода.

В геометрической трактовке модели Марковица используются так называемые кривые безразличия. Кривые безразличия показывают зависимость доходности и риска при постоянных уровнях полезности и строятся из функции полезности, связывающей полезность с доходностью и риском.

В теории инвестиционного портфеля обычно предполагается, что предпочтения инвесторов описываются квадратной функцией полезности.[11]

, где

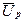- ожидаемая полезность портфеля;

- ожидаемая доходность портфеля;

- дисперсия (волатильность) доходности портфеля.

Такая функция соответствует нашим допущениям относительно поведения инвесторов. Рост ожидаемой доходности ведет к росту полезности. Рост риска, наоборот, уменьшает полезность. Два отрицательных члена в правой части уравнения обеспечивают постепенное замедление роста полезности по мере увеличения доходности.

При графическом представлении часто связывают доходность в процентах и среднеквадратическое отклонение. Дело в том, что размерность дисперсии (волатильности) – это квадрат процентов. Среднеквадратическое отклонение – корень квадратный из дисперсии – дает размерность сопоставимую с доходностью. Впрочем, графическое представление при этой замене меняется не существенно.

Квадратная форма функции полезности для инвестора, избегающего некомпенсируемого риска, дает кривую безразличия близкую к следующей

Рис. 3. Кривые безразличия