Равномерное приближение
Иногда ставится очень жесткое условие: во всех точках некоторого отрезка  отклонение многочлена
отклонение многочлена 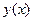 по абсолютной величине должно быть меньше заданной величины
по абсолютной величине должно быть меньше заданной величины 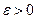 :
:
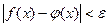 ,
, 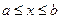 .
.
При выполнении такого условия говорят, что многочлен 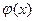 равномерно аппроксимирует функцию
равномерно аппроксимирует функцию  с точностью
с точностью  на отрезке
на отрезке  .
.
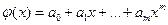 .
.
Определение. Абсолютным отклонением 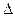 многочлена
многочлена 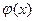 от функции
от функции  на отрезке
на отрезке  называется максимальное значение модуля разности между ними на данном отрезке:
называется максимальное значение модуля разности между ними на данном отрезке:
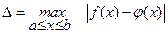 (рис. 6.2а.) (6.5)
(рис. 6.2а.) (6.5)
По аналогии вводится понятие среднеквадратичного отклонения при среднеквадратичном приближении функции 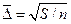
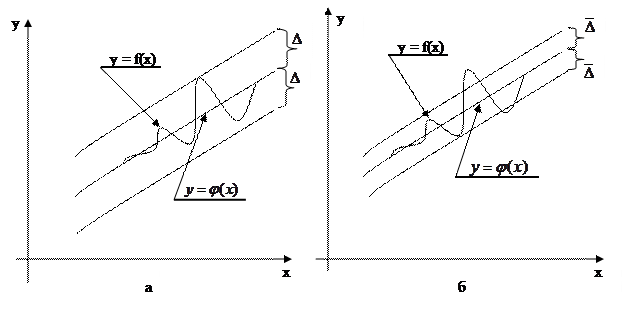
Рис. 6.2. К вопросу о приближениях: а – равномерное приближение, б – среднеквадратичное приближение.
Возможность построения многочлена, равномерно приближающего данную функцию, следует из теоремы Вейерштрасса об аппроксимации:
“Если функция  непрерывна на отрезке
непрерывна на отрезке  , то для любого
, то для любого 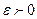 существует многочлен
существует многочлен 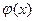 степени
степени 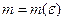 , абсолютное отклонение которого от функции
, абсолютное отклонение которого от функции  на отрезке
на отрезке  меньше
меньше  ”.
”.
В частности, если  на отрезке
на отрезке  разлагается в равномерно сходящийся степенной ряд, то в качестве аппроксимирующего многочлена можно взять частичную сумму этого ряда. (Такой подход широко используется, например, при вычислении на ЭВМ значений элементарных функций).
разлагается в равномерно сходящийся степенной ряд, то в качестве аппроксимирующего многочлена можно взять частичную сумму этого ряда. (Такой подход широко используется, например, при вычислении на ЭВМ значений элементарных функций).
Имеется также понятие наилучшего приближения функции f(x) многочленом φ(x) фиксированной степени  . В этом случае коэффициенты многочлена
. В этом случае коэффициенты многочлена 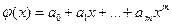 следует выбрать так, чтобы на заданном отрезке
следует выбрать так, чтобы на заданном отрезке  величина абсолютного отклонения (6.5) была минимальной.
величина абсолютного отклонения (6.5) была минимальной.
В этом случае многочлен 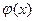 называется многочленом наилучшего равномерного приближения.
называется многочленом наилучшего равномерного приближения.
Существование и единственность многочлена наилучшего равномерного приближения вытекает из следующей теоремы:
Теорема. Для любой функции  , непрерывной на замкнутом ограниченном множестве
, непрерывной на замкнутом ограниченном множестве 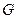 , и любого натурального
, и любого натурального  существует многочлен
существует многочлен 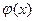 степени не выше
степени не выше  , абсолютное отклонение которого от функции
, абсолютное отклонение которого от функции  минимально, т.е.
минимально, т.е. 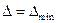 , причем такой многочлен единственный. Множество
, причем такой многочлен единственный. Множество 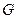 обычно представляет собой либо некоторый отрезок
обычно представляет собой либо некоторый отрезок  , либо конечную совокупность точек
, либо конечную совокупность точек 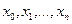 .
.
(Примером подобного разложения можно привести разложение элементарной функции  в тригонометрический ряд. Мы знаем из соответствующего курса математического анализа, что наилучшим приближением функции
в тригонометрический ряд. Мы знаем из соответствующего курса математического анализа, что наилучшим приближением функции  в виде тригонометрического ряда
в виде тригонометрического ряда
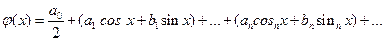
является ряд, где коэффициентами 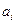 и
и 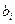 являются коэффициенты Фурье).
являются коэффициенты Фурье).
Многочлены Тейлора.
Определение. Будем говорить, что ф-я  принадлежит классу
принадлежит классу 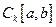 , и писать
, и писать 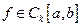 , если ф-ция
, если ф-ция 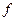 (х) определена на отрезке
(х) определена на отрезке  и имеет на нем непрерывные производные до порядка
и имеет на нем непрерывные производные до порядка  включительно.
включительно.
При 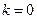 вместо
вместо 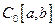 используют обозначение
используют обозначение 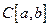 .
.
Запись 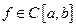 означает, что ф-ция f(x) непрерывна на отрезке
означает, что ф-ция f(x) непрерывна на отрезке 
В окрестности точки 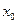 достаточно хорошее приближение ф-ции
достаточно хорошее приближение ф-ции  можно представить в виде многочлена Тейлора.
можно представить в виде многочлена Тейлора.
Пусть задана функция 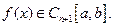
Многочленом Тейлора 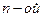 степени ф-ции f(x) в точке
степени ф-ции f(x) в точке 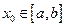 называется многочлен
называется многочлен 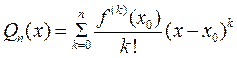 . (6.6)
. (6.6)
Многочлен (6.6) обладает тем свойством, что в точке 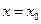 он сам и все его производные до порядка
он сам и все его производные до порядка  включительно совпадают с соответствующими производными функции
включительно совпадают с соответствующими производными функции 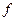 , т.е.
, т.е.
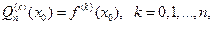
в чем легко убедиться, дифференцируя 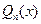 .
.
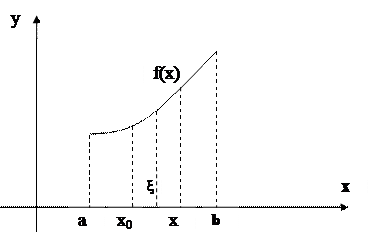 |
Рис.6.3. К приближению многочленом Тейлора.
Многочлен Тейлора хорошо приближает ф-цию  в окрестностях точки
в окрестностях точки 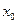 . Погрешность, возникающая при замене функции ее многочленом
. Погрешность, возникающая при замене функции ее многочленом 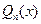 , выражается остаточным членом формулы Тейлора в форме Лагранжа
, выражается остаточным членом формулы Тейлора в форме Лагранжа
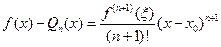 , (6.7)
, (6.7)
где 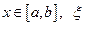 - точка, лежащая строго между
- точка, лежащая строго между  и
и 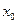 при
при 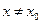 .
.
Так как по условию 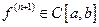 , то она ограничена на этом отрезке, т.е.
, то она ограничена на этом отрезке, т.е.
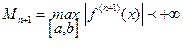 (6.8)
(6.8)
На основании (6.7) имеем
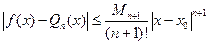 (6.9)
(6.9)
или 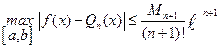 , (6.10)
, (6.10)
где 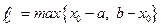 .
.
Определение. Пусть 
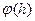 - некоторая функция переменной
- некоторая функция переменной 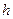 с конечной областью определения
с конечной областью определения 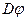 на полуоси
на полуоси 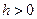 , причем
, причем 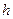 может принимать сколь угодно малые значения. Тогда, если существуют такие положительные
может принимать сколь угодно малые значения. Тогда, если существуют такие положительные 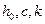 , что при всех
, что при всех 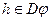 , удовлетворяющих условию
, удовлетворяющих условию 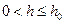 , выполняется неравенство
, выполняется неравенство
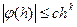 (6.11)
(6.11)
то пишут
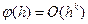 (6.12)
(6.12)
и говорят, что 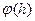 есть O большое от
есть O большое от 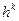 (при
(при 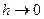 ).
).
Согласно данному определению выполняются и следующие очевидные свойства. Если, 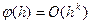 и
и 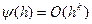 ,
,
причем области определения функций φ и ψ совпадают, т.е. Dφ= Dψ , то
φ(h) + ψ(h), т.е. (6.13)
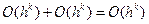 . (6.14)
. (6.14)
Наконец, если, 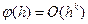 , то
, то 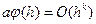 , где
, где  - постоянная, не зависящая от
- постоянная, не зависящая от 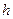 .
.
Определение. Аналогично, ф-ция 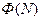 , заданная для всех натуральных
, заданная для всех натуральных 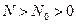 , есть O большое
, есть O большое 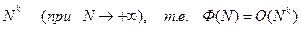 , если найдется такая постоянная
, если найдется такая постоянная 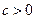 , что при всех натуральных
, что при всех натуральных 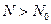
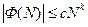 .
.
Возращаясь к остаточному члену ряда Тейлора, можем сказать, что погрешность приближения функции  многочленом Тейлора есть
многочленом Тейлора есть 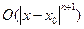 , а неравенство (6.10) служит оценкой максимаьной погрешности на всем отрезке
, а неравенство (6.10) служит оценкой максимаьной погрешности на всем отрезке  .
.
Из вышеприведенного очевидно, что погрешность аппроксимации многочленом Тейлора быстро убывает при 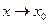 и резко возрастает на концах
и резко возрастает на концах  . Причем особенно сильно - у наиболее удаленного от
. Причем особенно сильно - у наиболее удаленного от 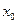 конца. Это есть основной недостаток использования ряда Тейлора при приближении функций.
конца. Это есть основной недостаток использования ряда Тейлора при приближении функций.
Тем не менее, многочлены Тейлора широко используются на практике для приближения функций. Особенно это касается ф-ций, у которых легко находятся старшие производные, а остаточный член 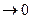 при
при 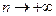 . Прежде всего это функции
. Прежде всего это функции 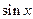 ,
, 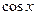 ,
, 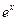 ,
, 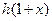 ,
, 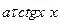 ,
, 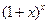 и другие.
и другие.
Пример. Аппроксимировать функцию 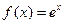 многочленом Тейлора на отрезке
многочленом Тейлора на отрезке 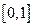 с абсолютной погрешностью, не превышающей
с абсолютной погрешностью, не превышающей 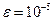 .
.
Решение. Выбираем 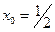 , т.е. в середине
, т.е. в середине 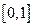 , с тем, чтобы минимизировать величину
, с тем, чтобы минимизировать величину 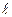 в составе оценки погрешности (6.10). Очевидно, что
в составе оценки погрешности (6.10). Очевидно, что
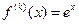 ,
, 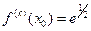 ,
, 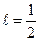 ,
, 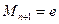 ,
,
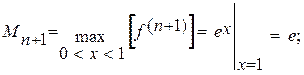
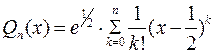 .
.
Согласно (6.10) при 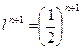 и Mn+1 = e
и Mn+1 = e
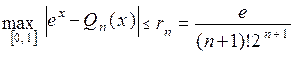

Для rn составим таблицу:
| n | ||||
| rn | 7,1·10-3 | 7,1·10-4 | 5,9·10-5 | 4,3·10-6 |
Видно, что 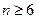 .
.
