Использование интерполяционных формул

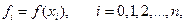Пусть задана в виде таблицы с

постоянным шагом .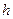

Запишем приближение функции 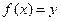с помощью интерполяционного

многочлена Ньютона.

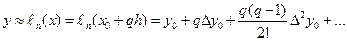
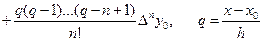… - безразмерная переменная.

Дифференцируя 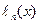по , и помня, что

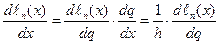, можно

получить формулы для вычисления производных любого порядка.

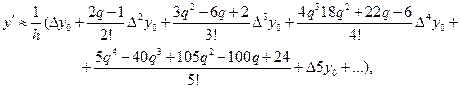
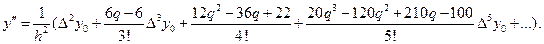
Пример. Вычислить в точке х = 0.1 первую и вторую производные функции, заданной таблицей.

х	у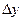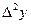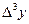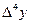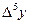
	1.2833
0.1	1.8107
0.2	1.3606
0.3	2.9577
0.4	3.5969
0.5	4.2833

Здесь 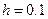, 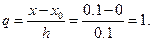Подставляя q в последние формулы, получим: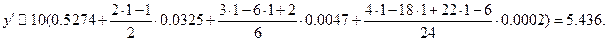

.

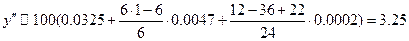Мы видим, что интерполяционные многочлены Ньютона дают выражения для производных через разности 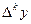. Но на практике проще выражать значения производных не через разности, а непосредственно через значения функции в узлах. Для получения таких формул удобно пользоваться формулой Лагранжа при постоянном шаге

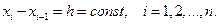
Запишем интерполяционный многочлен Лагранжа 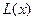и его остаточный член 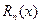для случая трёх узлов интерполяции (n = 2) и найдем их производные: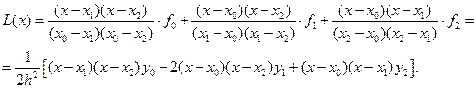

Остаточный член полинома Лагранжа (см.6.26) имеет вид

.

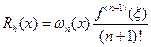Выше мы записывали остаточный член с использованием функции

.

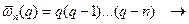
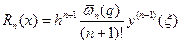Полагая, что 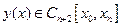, получаем:

.

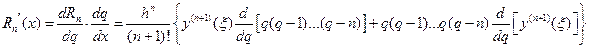При 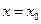и, следовательно, при 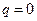и, учитывая, что

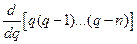
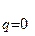
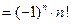, будем иметь:

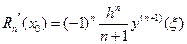. (12.8 а)

Так как 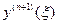во многих случаях трудно оценить, то при h малом приближенно полагают:

.

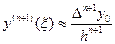Следовательно, 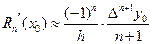. (12.8 б)

Аналогично может быть найдена погрешность 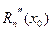для второй производной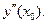

Остаточный член полинома Лагранжа (см.6.26) имеет вид

.

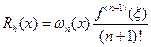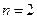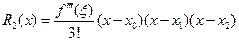Так как здесь , то , где 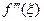- значение производной третьего порядка в некоторой внутренней точке .

,

.

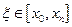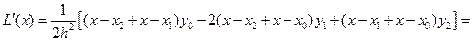
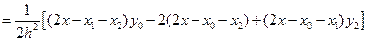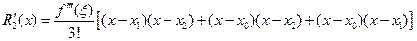Сейчас мы можем найти значение производной в любом узле интерполяции

отрезка .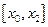

Запишем для наглядности последовательность вычисления производной

.

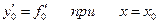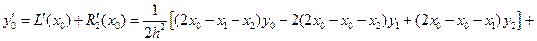
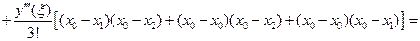
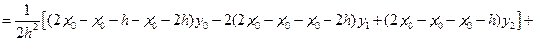
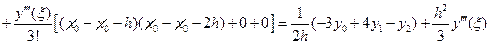
Проведя аналогичные вычисления, можно получить значения

:

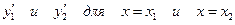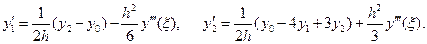
Продолжая подобные вычисления для случая четырех узлов 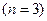, получают следующие приближения производных:

,

,

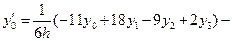
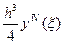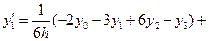
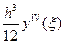(12.9)

,

.

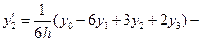
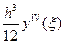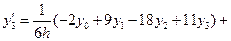
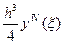В случае пяти узлов 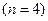получают

,

,

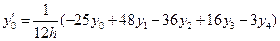
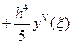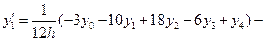
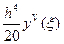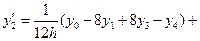
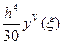, (12.10)

,

.

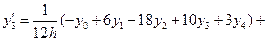
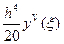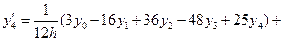
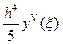Из приведенных формул видим, что, используя значения функции в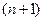

узле, получаем приближения производных 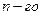порядка.

Кроме того, обратим внимание на то, что при четных ( 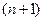узлов)

наиболее простые выражения и наименьшие коэффициенты в остаточных членах получаются для производных в средних (центральных) узлах

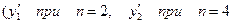и т. д.).

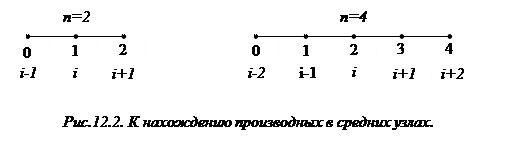Для этих двух случаев формулы можно обобщить. Придадим 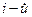номер

центральному узлу:

;

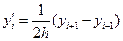
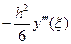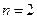
(12.11)

.

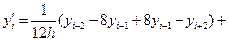
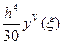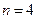
С помощью интерполяционных полиномов Лагранжа можно получить приближения и для старших производных. Приведем эти приближения.

В случае трех узлов интерполяции :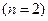

;

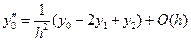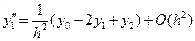; (12.12)

.

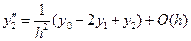В случае четырех узлов :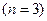

;

;

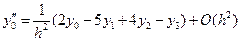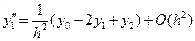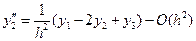; (12.13)

.

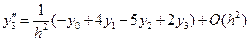В случае пяти узлов :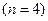

;

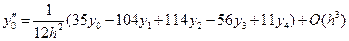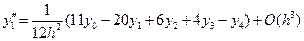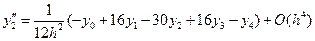; ; (12.14)

;

.

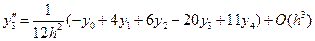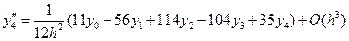Можно видеть, что приближение и вторых производных с помощью центральных разностей наиболее выгодны.