Метод Эйлера с пересчетом
Если в уравнении (17.6)
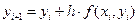
вместо 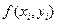 взять среднее арифметическое от
взять среднее арифметическое от 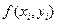 и
и 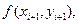
то вместо разностной схемы (17.6) мы получим:
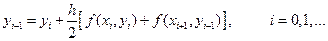 (17.8)
(17.8)
Полученная схема получилась неявной, поскольку искомое значение 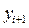 входит в обе части соотношения. Так как точного значения
входит в обе части соотношения. Так как точного значения 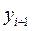 мы не можем знать, то вместо него мы можем взять его приближение
мы не можем знать, то вместо него мы можем взять его приближение 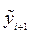 , вычисляемое по формуле (17.6)
, вычисляемое по формуле (17.6)
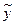
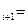
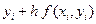 . (17.9)
. (17.9)
Подставив 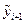 вместо
вместо 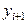 в (17.8), получим новое выражение для вычисления
в (17.8), получим новое выражение для вычисления 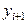
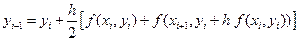 . (17.10)
. (17.10)
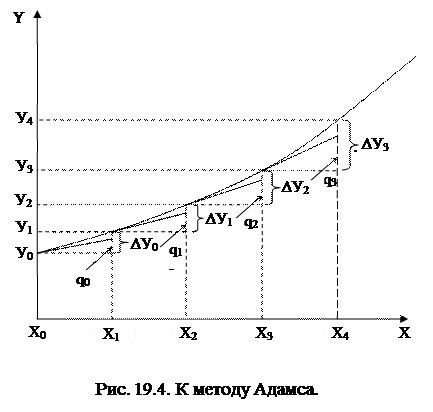
Последние рекуррентные соотношения представляют метод Эйлера с пересчетом. Этот метод имеет второй порядок точности. На рисунке дана геометрическая интерпретация первого шага вычислений при решении задачи Коши методом Эйлера с пересчетом.
 |
777777&&&&&uuUUU
Касательная к кривой 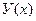 в точке
в точке 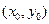 проводится с угловым коэффициентом
проводится с угловым коэффициентом
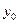 '
' 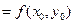 .
.
С ее помощью методом Эйлера найдено значение 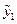 , которое используется затем для определения наклона касательной
, которое используется затем для определения наклона касательной 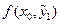 в точке
в точке 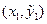 . Отрезок с таким наклоном заменяет первоначальный отрезок касательной от точки
. Отрезок с таким наклоном заменяет первоначальный отрезок касательной от точки 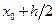 до точки
до точки 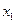 .
.
В результате получается уточненное значение искомой функции 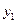 в этой точке.
в этой точке.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Метод Рунге-Кутта. Очевидно, что значение 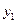 , полученное с помощью метода Эйлера менее точно, чем
, полученное с помощью метода Эйлера менее точно, чем 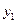 , полученное по схеме с пересчетом. Но схема с пересчетом может быть тоже улучшена. Сегодня наиболее оптимальным с точки зрения компромисса между объемом вычислений и достигаемой точностью считается метод Рунге-Кутта. Алгоритм этого метода записывается в виде
, полученное по схеме с пересчетом. Но схема с пересчетом может быть тоже улучшена. Сегодня наиболее оптимальным с точки зрения компромисса между объемом вычислений и достигаемой точностью считается метод Рунге-Кутта. Алгоритм этого метода записывается в виде
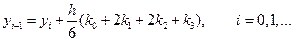
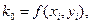
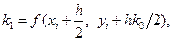
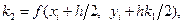
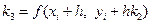 .
.
Видим, что метод Рунге-Кутта требует на каждом шаге четырехкратного вычисления правой части уравнения 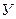 '
' 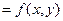 Для получения результатов с одинаковой точностью в методе Эйлера потребуется значительно меньший шаг, чем в методе Рунге-Кутта.
Для получения результатов с одинаковой точностью в методе Эйлера потребуется значительно меньший шаг, чем в методе Рунге-Кутта.
Рассмотрим результаты решения примера различными методами.
Пример. Решить задачу Коши
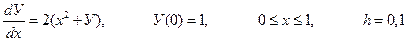
Решение. Можно решить это уравнение аналитическими методами. Для сравнения
решение это приводим: 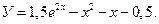
Проведем решение данной задачи численно с помощью рассмотренных выше методов. Результаты решений приведены в таблице. Из нее видно, что самым точным является решение, полученное методом Рунге-Кутта.
Видно, что при большом числе узлов метод Эйлера может привести к заметным погрешностям, в таких случаях предпочитают пользоваться численными методами высших порядков.
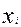 | Метод Эйлера | Метод Эйлера с пересчетом | Метод Рунге-Кутта | Точное решение |
| 0,1 | 1,2210 | 1,2221 | 1,2221 | |
| 0,2 | 1,4420 | 1,4923 | 1,4977 | 1,4977 |
| 0,3 | ||||
| 0,4 | 2,1041 | 2,2466 | 2,2783 | 2,2783 |
| 0,5 | ||||
| 0,6 | 3,1183 | 3,4176 | 3,5201 | 3,5202 |
| 0,7 | ||||
| 0,8 | 4,6747 | 5,2288 | 5,4894 | 5,4895 |
| 0,9 | ||||
| 1,0 | 7,0472 | 8,0032 | 8,5834 | 8,5836 |
В учебной литературе можно встретить различные модификации метода Рунге-Кутта. Рассмотренный нами метод называется метод Рунге-Кутта 4го порядка точности.
Погрешность 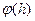 этого метода на шаге h равна
этого метода на шаге h равна
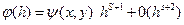 ( s-число коэффициентов в формуле).
( s-число коэффициентов в формуле).
У нас s=4, поэтому можно написать, что 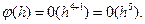 Погрешность вычисления в конце n го (интервала) шага
Погрешность вычисления в конце n го (интервала) шага
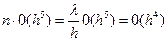 .
.
Наиболее употребительным одношаговым методом является метод Рунге-Кутта.
Метод Адамса.
Пусть требуется решить уравнение  '
'  .
.
Одним из разностных методов приближенного решения этой задачи является метод Адамса.
Задавшись шагом 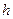 изменения аргумента, исходя из начальных условий
изменения аргумента, исходя из начальных условий 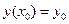 , находят следующие три значения искомой функции
, находят следующие три значения искомой функции 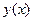 :
:
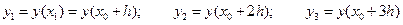 .
.
(Эти три значения можно получить любым методом, обеспечивающим нужную точность: методом Рунге-Кутта, с помощью разложения решения в степенной ряд и т.д., но не методом Эйлера ввиду его недостаточной точности).
С помощью чисел 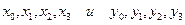 вычисляют величины
вычисляют величины
q0 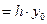 '
' 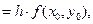
q1 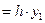 '
' 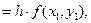
q2 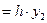 '
' 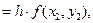
q3 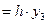 '
' 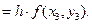
Далее составляют таблицу конечных разностей величин y и q.
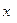 |  | Δ  | q | Δq | Δ2q | Δ3q |
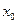 | 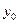 | q0 | ||||
Δ 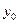 | Δq0 | |||||
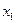 | 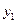 | q1 | Δ2q0 | |||
Δ 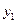 | Δq1 | Δ3q0 | ||||
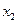 | 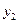 | q2 | Δ2q1 | |||
| Δу2 | Δq2 | |||||
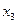 | 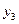 | q3 |
По формуле Адамса (Ньютона?) находим Δ 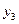
Δ 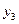 =q3+
=q3+ 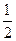 Δq2 +
Δq2 + 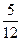 Δ2q1+
Δ2q1+ 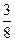 Δ3q0 ,
Δ3q0 ,
зная числа q3, Δq2, Δ2q1, Δ3q0 в нижней косой стороне таблицы
После этого можно найти 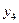 =
= 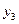 +Δ
+Δ 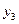 .
.
Зная теперь 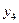 , вычисляют, q4
, вычисляют, q4 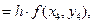 после чего может быть написана следующая косая строка: Δq3 = q4 - q3, Δ2q2 = Δq3 - Δq2, Δ3q1 = Δ2q2 - Δ2q1.
после чего может быть написана следующая косая строка: Δq3 = q4 - q3, Δ2q2 = Δq3 - Δq2, Δ3q1 = Δ2q2 - Δ2q1.
Новая косая строка позволяет нам вычислить по формуле Адамса значение Δ 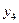
Δ 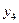 = q4+
= q4+ 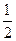 Δq3 +
Δq3 + 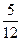 Δ2q2 +
Δ2q2 + 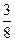 Δ3q1,
Δ3q1,
а следовательно, и 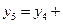 Δ
Δ 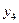 и т.д.
и т.д.
Пример: Используя метод Адамса, найти значение 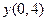 с точностью до 0,01 для
с точностью до 0,01 для
дифференциального уравнения  '=
'= 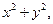
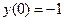 .
.
Решение: Найдем первые четыре члена разложения решения данного уравнения в ряд Тейлора в окрестности точки 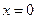
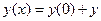 '
' 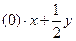 ''
'' 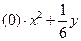 '''
''' 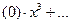
Согласно условию значения  '
' 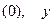 ''
'' 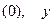 '''
''' 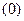 находим, последовательно дифференцируя данное уравнение:
находим, последовательно дифференцируя данное уравнение:
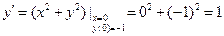 ,
,
 ''
'' 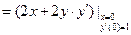
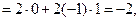
 '''
''' 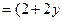 '2+2
'2+2 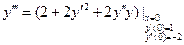
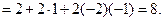
Таким образом, 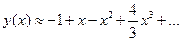
Вычисляем 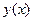 в точках
в точках 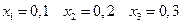 с одним запасным (третьим) знаком:
с одним запасным (третьим) знаком:  1=
1=  (0,1)=1+0,10,01+
(0,1)=1+0,10,01+ 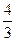
 0,001=0,9087≈0,909 ;
0,001=0,9087≈0,909 ;  2=
2=  (0,2)=1+0,20,04+
(0,2)=1+0,20,04+ 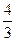
 0,008=0,2111,040=0,829;
0,008=0,2111,040=0,829;
 3=1+0,3=0,09+
3=1+0,3=0,09+ 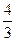
 0,027=1,09+0,3360=0,7540.
0,027=1,09+0,3360=0,7540.
Составим таблицу:
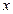 |  | Δ  | q | Δq | Δ2q | Δ3q |
| 1 | 0,1 | |||||
| 0,091 | 0,017 | |||||
| 0,1 | 0,909 | 0,083 | 0,006 | |||
| 0,080 | 0,011 | 0,002 | ||||
| 0,2 | 0,829 | 0,072 | 0,004 | |||
| 0,075 | 0,007 | |||||
| 0,3 | 0,754 | 0,065 | ||||
Здесь q0=0,1 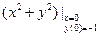 =0,1(0+1)=0,1,
=0,1(0+1)=0,1,
q1=0,1( 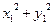 )=0,1(0,01+0,9092)=0,1(0,01+0,826)
)=0,1(0,01+0,9092)=0,1(0,01+0,826) 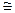 0,083,
0,083,
q2=0,1( 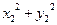 )=0,1(0,04+0,8292)=0,1(0,04+0,68)
)=0,1(0,04+0,8292)=0,1(0,04+0,68) 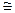 0,072,
0,072,
q3=0,1( 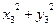 )=0,1(0,09+0,7542)=0,1(0,09+0,568)
)=0,1(0,09+0,7542)=0,1(0,09+0,568) 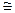 0,065.
0,065.
Теперь можно вычислить Δ 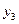 =q3+
=q3+ 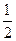 Δq2+
Δq2+ 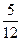 Δ2q1+
Δ2q1+ 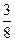 Δ3q0=0,065+
Δ3q0=0,065+ 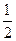 (0,007)+
(0,007)+ 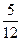 ·0,004+
·0,004+ 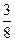 ·(0,002)=0,062.
·(0,002)=0,062.
Следовательно, 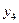 =
= 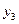 +Δ
+Δ 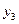 ≈0,754+0,062=0,692≈0,69.
≈0,754+0,062=0,692≈0,69.
(*) Оценка погрешности по А.С. Бахвалов и др. Численные методы, м. 1987г.
