IV. Основы теории вероятностей и элементы математической статистики

26.В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди 6 взятых наудачу деталей 4 стандартных.

Ответ:1.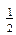

2.

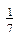
3.

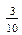
27.Два стрелка независимо друг от друга стреляют по мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,8; для второго – 0,4. После стрельбы в мишени обнаружена одна пробоина. Во сколько раз вероятность того, что попал в цель 1-й стрелок при наличии одной пробоины выше, чем для 2-го стрелка?

Ответ:1. в 2 раза

2. в 6 раз

3. в 4 раза

28.Во время футбольного матча на игровом поле находятся 23 человека. Верно ли, что вероятность того, что хотя бы у двоих из них день рождения в один день больше 0,5? Считаем, что в году 365 дней.

Ответ:1. искомая вероятность меньше 0,5

2. искомая вероятность равна 0,5

3. искомая вероятность больше 0,5

29.Слушателям программы «ФинТех» был предложен тест из 50-и вопросов, при этом на каждый вопрос дано три ответа, из которых только один верный. Сколько в среднем верных ответов дадут участники программы, если каждый раз они будут выбирать ответ случайным образом, даже не вникая в суть вопросов?

Ответ:1. примерно 17

2. примерно 25

3. примерно 10

30.Дана плотность вероятности случайной величины Х: 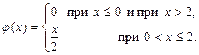. Найти вероятность того, что случайная величина Х примет значение из интервала [1; 2],

Ответ : 1. 3/4.

2. 1/2 .

3. 1.

31.Все значения равномерно распределённой случайной величины X лежат на отрезке 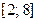. Найти вероятность попадания случайной величины X в промежуток .

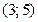Ответ : 1. 3/4.

2. 1/2 .

3. 1/3.

32.Случайная величина X подчинена закону Пуассона с математическим ожиданием, равным 3. Найти вероятность того, что случайная величина X принимает значение меньшее, чем её математическое ожидание.

Ответ:1. искомая вероятность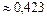

2. искомая вероятность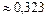

3. искомая вероятность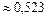

33.Случайная величина X подчинена нормальному закону с математическим ожиданием, равным 0. Вероятность попадания случайной величины X в интервал 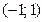равна 0,5. Найти среднее квадратическое отклонение случайной величины X.

Ответ:1. среднее квадратическое отклонение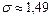

2. среднее квадратическое отклонение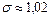

3. среднее квадратическое отклонение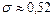

34.На уровне значимости 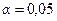проверить с помощью критерия Пирсона гипотезу о нормальном распределении случайной величины Х – выработки рабочих одного цеха, если известно распределение 50 рабочих цеха по выработке:

Выработка	100-110	110-120	120-130	130-140
Количество рабочих

(для упрощения вычислений даны выборочная средняя и выборочная дисперсия: , ).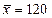

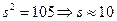Ответ:1. гипотеза о нормальном распределении отвергается

2. гипотеза о нормальном распределении не отвергается

3. для проверки гипотезы не достаточно данных