Лабораторная работа №9

Интерполяционный многочлен Лагранжа

Краткая теория

Интерполяционный многочлен Лагранжа используется для приближённого вычисления значений функции 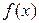, заданной своими значениями в узлах . Для произвольных (не обязательно равноотстоящих) узлов применяется формула:

или в другой форме:

где

Для равноотстоящих узлов таблицы (т.е. при выполнении равенства для всех ) применяется формула:

где

Решение одного варианта

1. Вычислить значение функции, заданной таблицей

x	y
0,05 0,10 0,17 0,25 0,30 0,36	0,050042 0,100335 0,171657 0,255342 0,309336 0,376403

при x=0.263.

Применим формулу Лагранжа для неравноотстоящих узлов:

Вычисления оформим в таблице:

	0,213	-0,05	-0,12	-0,20	-0,25	-0,31	-0,19809∙10	-256,2
	0,05	0,163	-0,07	-0,15	-0,20	-0,26	0,44499∙10	25547,7
	0,12	0,07	0,093	-0,08	-0,13	-0,19	-0,154365∙10	-111202
	0,20	0,15	0,08	0,013	-0,05	-0,11	0,1716∙10
	0,25	0,20	0,13	0,06	-0,037	-0,06	0,7215∙10
	0,31	0,26	0,19	0,11	0,06	-0,097	-0,980402∙10	-38392,7

Находим: ;

Следовательно, .

2. Вычислить значение функции, заданной таблицей

x	y
0,101 0,106 0,111 0,116 0,121 0,126	1,26183 1,27644 1,29122 1,30617 1,32130 1,32660

при x=0,1157

Узлы интерполяции равноотстоящие, поэтому применим формулу Лагранжа в соответствующем виде:

,

где , , ,

, .

Дальнейшие вычисления располагаем в таблице:

i			q-i
	0,101 0,106 0,111 0,116 0,121 0,126	1,26183 1,27644 1,29122 1,30617 1.32130 1,32660	2,94 1,94 0,94 -0,06 -1.06 -2,06	-120 -12 -24	-352,8 46,56 -11,28 -0,72 25,44 -247,2	-0,0035766 0,0274149 -03,1144691 -1,8141250 0,0519379 -0,0054069

Получаем ; = -1,858226.

Следовательно, f(0,1157)=1,30527.

Задание

Функция задана таблицей значений в точках . Требуется найти приближённое значение функции при данном значении аргумента x с помощью интерполяционного многочлена Лагранжа, если функция задана:

1)в неравноотстоящих узлах таблицы; 2)в равноотстоящих узлах таблицы.

Варианты к заданию 1

0,43 0,48 0,55 0,62 0,70 0,75     0,02 0,08 0,12 0,17 0,23 0,30	1,63597 1,73234 1,87686 1,03345 1,22846 1,35973     1,02316 1,09590 1,14725 1,21483 1,30120 1,40976	№ варианта	X 0,702 0,521 0,645 0,736 0,608 0,715 0,534   0,102 0,114 0,125 0,203 0,154 0,235 0.214
0,35 0,41 0,47 0,51 0,64 0,67     0,41 0,46 0,52 0,60 0,65 0,72	2,73951 2,30080 1,96864 1,78776 1,59502 1,89865     2,57418 2,23513 2,09336 1,36203 1,74926 1,62098		0,453 0,482 0,552 0,436 0,578 0,398 0,447   0,616 0,478 0,665 0,573 0,637 0,421 0,589

Варианты к заданию 2

1,375 1,380 1,385 1,390 1,395 1,400     0,115 0,120 0,125 0,130 0,135 0,140     0,115 0,120 0,125 0,130 0,135 0,140     0,150 0,155 0,160 0,165 0,170 0,175

5,04192 5,17744 5,32016 5,47068 5,69268 5,79738     8,65729 8,29329 7,95829 7,64893 7,36235 7,09613     8,65729 8,29329 7,95829 7,64893 7,36235 7,09613     6,61659 6,39989 6,19650 5,00551 5,82558 5,65583

№ варианта

X 1,3832 1,3926 1,3862 1,3934 1,3866 1,3791 1,3834   0,1264 0,1315 0,1232 0,1334 0,1285 0,1198 0,1234   0,1221 0,1211 0,1262 0,1342 0,1325 0,1319 0,1254   0,1538 0,1575 0,1644 0,1676 0,1738 0,1703 0,1722

Лабораторная работа №10

Интерполяционный многочлен Ньютона

Краткая теория

Пусть необходимо решить задачу интерполирования. Для ее решения воспользуемся интерполяционным многочленом Ньютона. В случае равноотстоящих узлов интерполяции, т.е., когда , интерполяционный многочлен Ньютона имеет вид

(1)

Формула (1) – интерполяционная формула Ньютона «интерполирования вперед», она удобна при интерполировании функций в точках , близких к . Для вычисления значения функции с помощью многочлена Ньютона при равноотстоящих узлах полагаем и формула Ньютона принимает вид

При интерполировании функций для значений x, близких к наибольшему узлу x_n используют формулу «интерполирования назад». При равноотстоящих узлах формула интерполирования назад имеет вид

обозначим ее формулой (3)

или

где

Решение одного варианта

Функция y(x) задана с помощью таблицы:

x	y
1.215 1.220 1.225 1.230 1.235 1.240 1.245 1.250 1.255 1.260	0.106044 0.106491 0.106935 0.107377 0.107818 0.108257 0.108696 0.109134 0.109571 0.110008

Найти значения функции y(x) при следующих значениях аргумента:

x₁=1.2173,

x₂=1.253,

x₃=1.210,

x₄=1.270.

Составим таблицу конечных разностей:

i	x	y
	1.215 1.220 1.225 1.230 1.235 1.240 1.245 1.250 1.255 1.260	0.106044 0.106491 0.106935 0.107377 0.107818 0.108257 0.108696 0.109134 0.109571 0.110008	0.000447 0.000444 0.000442 0.000441 0.000439 0.000439 0.000438 0.000437 0.000437 -	-0.000003 -0.000002 -0.000001 -0.000002 -0.000001 -0.000001 - -

Ограничиваемся разностями второго порядка, так как они практически постоянны. При x=1.2173 и x=1.210 пользуемся формулой Ньютона «интерполирования вперед»: , где .

Если x=1.2173, то: q=(1.2173-1.215)/0.005=0.46;

P(1.2173)=0.106044+0.46×(0.46-1)×(-0.000003)/2=0.106044+

+0.0002056+0.0000004=0.1106250.

Если x=1.210, то: q=(1.210-1.215)/0.005=-1;

P(1.210)=1.106044+(-1) ×0.000447-0.000003=0.105594.

При x=1.253 и x=1.270 пользуемся формулой Ньютона «интерполирования назад»:

, где .

Если x=1.253, то: q=(1.253-1.260)/0.005=-1.4;

P(1.253)=0.110008+(-1.4) ×(-1.4+1) ×0=0.110008-0.000612=0.109396.

Если x=1.270, то: q=(1.270-1.260)/0.005=2;

P(1.270)=0.110008+2 ×0.000437+2 ×3 ×(-0.000001)/2=0.110879.

Ответ: f(1.2173)»0.106250; f(1.253)»0.109396;

f(1.210)»0.105594; f(1.270)»0.110879.

Задание

Используя первую или вторую интерполяционную формулу Ньютона, вычислить значение функции при данных значениях аргумента.

x	y	№ вар	Значения аргумента
x1	x2	x3	x4
1.415 1.420 1.425 1.430 1.435 1.440 1.445 1.450 1.455 1.460	0.888551 0.889599 0.890637 0.891667 0.892687 0.893698 0.895693 0.896677 0.897653 0.898619		1.4161 1.4179 1.4263 1.4238 1.4082 1.4205 1.4058	1.4625 1.4633 1.4575 1.4612 1.4644 1.4621 1.4598	1.4135 1.4124 1.410 1.4118 1.4136 1.4107 1.4112	1.470 1.4655 1.4662 1.4658 1.4680 1.4672 1.4697

x	y	№ вар	Значения аргумента
x1	x2	x3	x4
1.415 1.420 1.425 1.430 1.435 1.440 1.445 1.450 1.455 1.460	0.888532 0.889578 0.890629 0.891641 0.892678 0.893702 0.895106 0.896542 0.897664 0.898613		1.4158 1.4184 1.4272 1.4213 1.4195 1.4257 1.4156	1.4622 1.4571 1.4536 1.4558 1.4609 1.4646 1.4678	1.4147 1.4139 1.414 1.4142 1.4136 1.4240 1.4211	1.465 1.4612 1.4608 1.4670 1.4658 1.4710 1.4709
x	y	№ вар	Значения аргумента
x1	x2	x3	x4
1.101 1.106 1.111 1.116 1.121 1.126 1.131 1.136 1.141 1.146	0.888551 0.889599 0.890637 0.891667 0.892687 0.893698 0.895693 0.896677 0.897653 0.898619		1.1026 1.1035 1.1074 1.1014 1.1029 1.1046 1.1012	1.1440 1.1492 1.1485 1.1429 1.1435 1.1448 1.1427	1.099 1.096 1.1006 1.0982 1.1008 1.1002 1.0989	1.161 1.153 1.156 1.152 1.154 1.155 1.159

x	y	№ вар	Значения аргумента
x1	x2	x3	x4
0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60	0.860708 0.818731 0.778801 0.740818 0.704688 0.670320 0.637628 0.606531 0.576950 0.548812		0.1511 0.1535 0.1525 0.1642 0.1683 0.2014 0.1698	0.7250 0.7333 0.6730 0.6238 0.6386 0.6642 0.7123	0.1430 0.100 0.1455 0.1256 0.1387 0.1472 0.1356	0.80 0.7540 0.85 0.7621 0.7354 0.720 0.7876