Метод простой итерации
Пусть имеется система линейных уравнений вида:
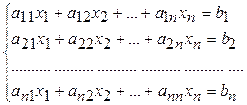 (1)
(1)
Приведем систему (1) к равносильной ей системе вида x=Fx. В развернутом виде новая система выглядит так:
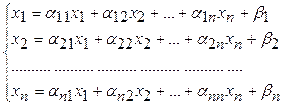 (2)
(2)
или в сокращенной записи 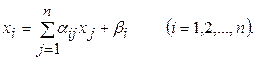 О системе (2) говорят, что она «приведена к нормальному виду».
О системе (2) говорят, что она «приведена к нормальному виду».
Правая часть системы (2) определяет отображение (обозначим его F):
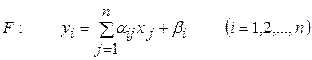 , (3)
, (3)
преобразующее точку 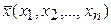 n-мерного векторного пространства в точку
n-мерного векторного пространства в точку 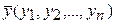 того же пространства. Используя отображение (3) и выбрав начальную точку
того же пространства. Используя отображение (3) и выбрав начальную точку 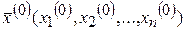 , можно построить итерационную последовательность точек n-мерного пространства:
, можно построить итерационную последовательность точек n-мерного пространства:
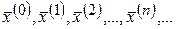 (4)
(4)
Если отображение F является сжимающим, то эта последовательность сходится и ее предел является решением системы (2) и тем самым исходной системы.
Решение вопроса о сжимаемости отображения (3) зависит от способа метризации пространства (т.е. определения расстояния между n-мерными векторами).
Пусть 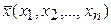 и
и 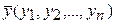 - две точки n-мерного пространства. Для применения метода итерации систему линейных уравнений удобно «погрузить» в пространство с одной из трех следующих метрик:
- две точки n-мерного пространства. Для применения метода итерации систему линейных уравнений удобно «погрузить» в пространство с одной из трех следующих метрик:
а) 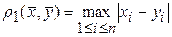 ; (5)
; (5)
б) 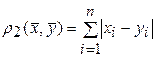 ; (6)
; (6)
в) 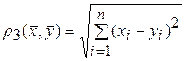 . (7)
. (7)
Тогда условия сжимаемости отображения (3) в пространствах с метриками 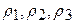 выражаются через коэффициенты при неизвестных системы (2):
выражаются через коэффициенты при неизвестных системы (2):
а) в пространстве метрикой 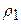 :
:
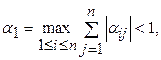 (8)
(8)
б) в пространстве метрикой 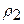 :
:
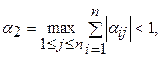 (9)
(9)
в) в пространстве метрикой 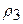 :
:
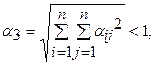 (10)
(10)
Алгоритм метода
1) Переписать систему в виде (2). Для обеспечения условий сходимости нужно получить систему вида (2) так, чтобы коэффициенты 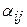 при неизвестных в правой части системы были существенно меньше единицы. Этого можно достичь, если исходную систему вида (1) с помощью равносильных преобразований привести к системе, у которой абсолютные величины коэффициентов, стоящих на главной диагонали, больше абсолютных величин каждого из других коэффициентов при неизвестных в соответствующих уравнениях (такую систему называют системой с преобладающими диагональными коэффициентами). Если теперь разделить все уравнения на соответствующие диагональные коэффициенты и выразить из каждого уравнения неизвестное с коэффициентом, равным единице, будет получена система вида (2), у которой все
при неизвестных в правой части системы были существенно меньше единицы. Этого можно достичь, если исходную систему вида (1) с помощью равносильных преобразований привести к системе, у которой абсолютные величины коэффициентов, стоящих на главной диагонали, больше абсолютных величин каждого из других коэффициентов при неизвестных в соответствующих уравнениях (такую систему называют системой с преобладающими диагональными коэффициентами). Если теперь разделить все уравнения на соответствующие диагональные коэффициенты и выразить из каждого уравнения неизвестное с коэффициентом, равным единице, будет получена система вида (2), у которой все 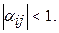
2) Выполнение этого условия необходимо, но недостаточно для удовлетворения условий сжимаемости (8)-(10). Если после указанных выше преобразований ни одно из этих условий не выполняется, следует возвратиться к исходной системе и попытаться выполнить преобразования так, чтобы добиться лучшего эффекта. Для этого имеются специальные приемы, но они не универсальны. Иначе говоря, вполне возможно, что для некоторой конкретной системы метод итераций окажется неприменим.
3) Результатом установления одного из условий (8)-(10) является получение значения α, которое затем находит применение в формуле оценке точности k-го приближения. После того как сходимость установлена, можно приступить к выполнению вычислений.
4) За начальное приближение обычно берется столбец свободных членов системы (2). Момент прекращения итерационного процесса при достижении заданной точности результата ε устанавливается формулой:
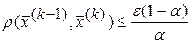 , (11)
, (11)
где ρ – метрика, по которой была установлена сходимость и получено соответствующее значение α.
Решение одного варианта
Решить систему линейных уравнений
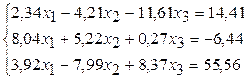
методом простой итерации с точностью ε=1·10-4.
1) Получим систему с преобладающими диагональными коэффициентами. Для этого в качестве первого уравнения возьмем второе, третьего – первое, второго – сумму первого уравнения с третьим:
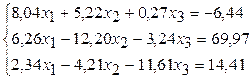 .
.
2) Разделим каждое уравнение на свой диагональный коэффициент и выразим из каждого уравнения диагональное неизвестное:
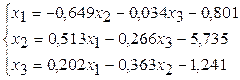 .
.
3) Проверим одно из условий сходимости.
а) Попробуем установить сходимость по метрике 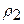 . Заметим, что максимальной суммой модулей коэффициентов по столбцам будет сумма модулей коэффициентов при х2. Однако эта сумма не удовлетворяет условию (9): 0,649+0,363>1.
. Заметим, что максимальной суммой модулей коэффициентов по столбцам будет сумма модулей коэффициентов при х2. Однако эта сумма не удовлетворяет условию (9): 0,649+0,363>1.
Невыполнение одного из условий еще не означает, что метод итераций применить нельзя.
б) Попробуем установить сходимость в пространстве с евклидовой метрикой (10). Имеем:
0,6492+0,0342+0,5132+0,2662+0,2022+0,3632=
=0,422+0,001+0,263+0,071+0,041+0,131=0,929<1.
Следовательно, итерационный процесс в евклидовом пространстве сходится, причем α= 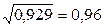 .
.
4) Для достижения точности ε=1·10-4 приближения будем находить до тех пор, пока не выполнится неравенство 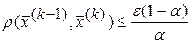 , где
, где 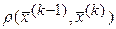 - расстояние между двумя последними соседними приближениями в смысле евклидовой метрики, ε=1·10-4, α=0,96,
- расстояние между двумя последними соседними приближениями в смысле евклидовой метрики, ε=1·10-4, α=0,96, 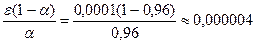 .
.
Оформим вычисления в таблице:
| х1 | х2 | х3 | b | |
| -0,649 | -0,034 | -0,801 | ||
| 0,513 | -0,266 | -5,735 | ||
| 0,202 | -0,363 | -1,241 | ||
| № ите-рации | х1 | х2 | х3 | расстояние |
| 0,000000 | 0,000000 | 0,000000 | ||
| -0,801000 | -5,735000 | -1,241000 | 5,922154 | |
| 2,963209 | -5,815807 | 0,679003 | 4,226371 | |
| 2,950373 | -4,395489 | 1,468706 | 1,625146 | |
| 2,001736 | -4,612135 | 0,950538 | 1,102427 | |
| 2,159957 | -4,960952 | 0,837556 | 0,399340 | |
| 2,390181 | -4,849732 | 0,996137 | 0,300867 | |
| 2,312607 | -4,773809 | 1,002269 | 0,108718 | |
| 2,263125 | -4,815236 | 0,959040 | 0,077675 | |
| 2,291481 | -4,829121 | 0,964082 | 0,031973 | |
| 2,300321 | -4,815916 | 0,974850 | 0,019196 | |
| 2,291385 | -4,814246 | 0,971842 | 0,009576 | |
| 2,290403 | -4,818030 | 0,969431 | 0,004594 | |
| 2,292941 | -4,817892 | 0,970606 | 0,002800 | |
| 2,292811 | -4,816903 | 0,971069 | 0,001100 | |
| 2,292153 | -4,817092 | 0,970684 | 0,000786 | |
| 2,292290 | -4,817327 | 0,970619 | 0,000279 | |
| 2,292444 | -4,817240 | 0,970732 | 0,000210 | |
| 2,292384 | -4,817191 | 0,970732 | 0,000078 | |
| 2,292352 | -4,817222 | 0,970702 | 0,000054 | |
| 2,292373 | -4,817230 | 0,970707 | 0,000023 | |
| 2,292378 | -4,817221 | 0,970714 | 0,000013 | |
| 2,292372 | -4,817220 | 0,970711 | 0,000007 | |
| 2,292371 | -4,817222 | 0,970710 | 0,000003 |
Итерационный процесс окончен. Число итераций = 24.
Ответ: х1≈2,2924, х2≈4,8172, х3≈0,9707.
Задание
Используя метод простых итераций, решить систему уравнений с точностью до 0,0001 с оценкой погрешности метода по одной из метрик с применением оценочной формулы (11).
Варианты заданий
| № вари-анта | i | ai1 | ai2 | ai3 | b |
| 0,21 | -0,45 | -0,20 | 1,91 | ||
| 0,30 | 0,25 | 0,43 | 0,32 | ||
| 0,60 | -0,35 | -0,25 | 1,83 | ||
| -3 | 0,5 | 0,5 | -56,5 | ||
| 0,5 | -6,0 | 0,5 | -100 | ||
| 0,5 | 0,5 | -3 | -210 | ||
| 0,45 | -0,94 | -0,15 | -0,15 | ||
| -0,01 | 0,34 | 0,06 | 0,31 | ||
| -0,35 | 0,05 | 0,63 | 0,37 | ||
| 0,63 | 0,05 | 0,15 | 0,34 | ||
| 0,15 | 0,10 | 0,71 | 0,42 | ||
| 0,03 | 0,34 | 0,10 | 0,32 | ||
| -0,20 | 1,60 | -0,10 | 0,30 | ||
| -0,30 | 0,10 | -1,50 | 0,40 | ||
| 1,20 | -0,20 | 0,30 | -0,60 | ||
| 0,30 | 1,20 | -0,20 | -0,60 | ||
| -0,10 | -0,20 | 1,60 | 0,30 | ||
| 0,05 | 0,34 | 0,10 | 0,32 | ||
| 0,20 | 0,44 | 0,81 | 0,74 | ||
| 0,58 | -0,29 | 0,05 | 0,02 | ||
| 0,05 | 0,34 | 0,10 | 0,32 | ||
| 6,36 | 11,75 | -41,40 | |||
| 7,42 | 19,03 | 11,75 | -49,49 | ||
| 5,77 | 7,48 | 6,36 | -27,67 | ||
| -9,11 | 1,02 | -0,73 | -1,25 | ||
| 7,61 | 6,25 | ,-2,32 | 2,33 | ||
| -4,64 | 1,13 | -8,88 | -3,75 | ||
| -9,11 | -1,06 | -0,67 | -1,56 | ||
| 7,61 | 6,35 | -2,42 | 2,33 | ||
| -4,64 | 1,23 | -8,88 | -3,57 | ||
| 1,02 | -0,73 | -9,11 | -1,25 | ||
| 6,25 | -2,32 | 7,62 | 2,33 | ||
| 1,13 | -8,88 | 4,64 | -3,75 | ||
| 0,06 | 0,92 | 0,03 | -0,82 | ||
| 0,99 | 0,01 | 0,07 | 0,66 | ||
| 1,01 | 0,02 | 0,99 | -0,98 | ||
| 0,10 | -0,07 | -0,96 | -2,04 | ||
| 0,04 | -0,99 | -0,85 | -3,73 | ||
| 0,91 | 1,04 | 0,19 | -1,67 | ||
| 0,62 | 0,81 | 0,77 | -8,18 | ||
| 0,03 | -1,11 | -1,08 | 0,08 | ||
| 0,97 | 0,02 | -1,08 | 0,06 | ||
| 0,63 | -0,37 | 1,76 | -9,29 | ||
| 0,90 | 0,99 | 0,05 | 0,12 | ||
| 0,13 | -0,95 | 0,69 | 0,69 | ||
| 0,98 | 0,88 | -0,24 | 1,36 | ||
| 0,16 | -0,44 | -0,88 | -1,27 | ||
| 9,74 | -10,00 | 1,71 | -5,31 | ||
| 0,21 | -0,94 | -0,94 | -0,25 | ||
| 0,98 | -0,19 | 0,93 | 0,23 | ||
| 0,87 | 0,87 | -0,14 | 0,33 | ||
| 3,43 | 4,07 | -106,00 | 46,8 | ||
| 74,4 | 1,84 | -1,85 | -26,5 | ||
| 3,34 | 94,3 | 1,02 | 92,3 | ||
| 0,66 | 0,44 | 0,22 | -0,58 | ||
| 1,54 | 0,74 | 1,54 | -0,32 | ||
| 1,42 | 1,42 | 0,86 | 0,83 | ||
| 0,78 | -0,02 | -0,12 | 0,56 | ||
| 0,02 | -0,86 | 0,04 | 0,77 | ||
| 0,12 | 0,44 | -0,72 | 1,01 | ||
| 2,70 | 9,30 | 1,30 | 2,10 | ||
| 3,50 | 1,70 | 2,80 | 1,70 | ||
| 4,10 | 5,80 | -1,70 | 0,80 | ||
| 1,70 | -2,80 | 1,90 | 0,70 | ||
| 2,10 | 3,40 | 1,80 | 1,11 | ||
| 4,20 | -1,70 | 1,30 | 2,80 | ||
| -1 | -1 | 11,33 | |||
| -1 | -1 | ||||
| -1 | -1 | ||||
| 0,24 | -0,08 | ||||
| 0,09 | -0,15 | ||||
| 0,04 | -0,08 | ||||
| -1 | -3 | ||||
| -2 | |||||
| -4 | |||||
| -2 | -2 | ||||
| -1 | -2 | ||||
| -1 | -1 | ||||
| 2,00 | 10,00 | 1,00 | 13,00 | ||
| 10,00 | 1,00 | 1,00 | 12,00 | ||
| 2,00 | 2,00 | 10,00 | 14,00 |
