Основные положения теории подобия для процессов теплообмена
Для обобщения экспериментальных данных и распространения их на многие аналогичные процессы используется теория подобия (теория теплового моделирования), на основе которой изучение сложного и громоздкого процесса заменяется изучением простой, но подобной модели.
Теория подобия – есть учение о подобных явлениях.
Два физических процесса будут подобными если они происходят в геометрически подобных системах, а отношение одноименных параметров (линейные размеры, скорость, плотность, температура и т.д.) в сходственных точках систем есть постоянные величины, называемыми константами подобия.
Следовательно, создание подобной модели любого явления связано с соблюдением геометрического, теплового и гидродинамического подобия.
Теория подобия основана на трех теоремах подобия. Первая и вторая теоремы описывают свойства явлений, подобия которых известны, а третья теорема устанавливает необходимые признаки, по которым устанавливается подобие явлений.
Первая теорема подобия доказывает, что подобные явления имеют одинаковые критерии подобия.
Критериями подобия называются безразмерные комплексы, составленные из величин, характеризующих явление. Критерии не выбираются произвольно, а вытекают из дифференциальных уравнений, описывающих данные явления и называются именами ученых, первыми предложивших и обосновавших их применение.
Для описания стационарного процесса конвективного теплообмена наиболее часто применяются следующие критерии подобия.
Критерий Нуссельта, или критерий теплоотдачи, характеризует отношение величины теплового потока, передаваемого за счет конвективного теплообмена по нормали к твердой стенке – к тепловому потоку, передаваемому теплопроводностью через слой толщиной 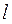 в тех же условиях:
в тех же условиях:
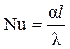 , (2.3)
, (2.3)
где 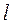 – характерный размер процесса теплообмена (для труб
– характерный размер процесса теплообмена (для труб 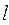 – диаметр), м.
– диаметр), м.
Критерий Рейнольдса, или критерий гидродинамического подобия, характеризует отношение сил инерции и сил вязкости (вязкостного трения) в потоке движущейся жидкости и определяет гидродинамический режим движения потока жидкости:
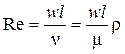 , (2.4)
, (2.4)
где w – скорость движения жидкости, м/с;
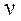 – коэффициент кинематической вязкости жидкости, м2/с;
– коэффициент кинематической вязкости жидкости, м2/с;
µ – коэффициент динамической вязкости жидкости, кг/(м·с);
ρ – плотность жидкости (газа), кг/м3;
Опытом установлено, что при Re<2300 влияние сил вязкости на характер движения является преобладающим и режим движения носит устойчивый ламинарный характер, при 2300<Re<10000 режим движения неустойчивый, переходный, и при Re>10000 преобладают силы инерции, и режим движения является устойчиво турбулентным.
Критерий Пекле, или критерий теплообмена, характеризует отношение величины теплового потока, переносимого конвекцией вдоль течения, к тепловому потоку, передаваемому теплопроводностью по направлению нормали к твердой поверхности:
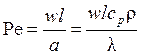 , (2.6)
, (2.6)
где 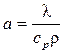 – коэффициент температуропроводности, м2/с;
– коэффициент температуропроводности, м2/с;
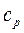 – теплоемкость жидкости при постоянном давлении, Дж/(кг·К).
– теплоемкость жидкости при постоянном давлении, Дж/(кг·К).
Критерий Прандтля, или критерий физических свойств жидкости, который определяет подобие температурных и скоростных полей в потоке жидкости (при Pr=1 поля температур и скоростей течения точно подобны):
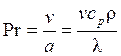 . (2.7)
. (2.7)
Связь между критериями:
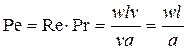 .
.
Критерий Грасгофа, или критерий подъемной силы, характеризует соотношение подъемной силы, возникающей при свободной конвекции, с силами инерции и вязкостного трения в жидкости:
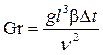 , (2.8)
, (2.8)
где g = 9,81 – ускорение силы тяжести, м/с2;
β – температурный коэффициент объемного расширения жидкости при постоянном давлении, 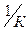 . Для газов
. Для газов 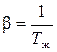 ;
;
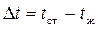 – температурный напор при конвективном теплообмене, К;
– температурный напор при конвективном теплообмене, К;
Для вычисления критериев подобия, обычно, используют усредненные значения основных физических параметров (скорости, температуры и т. д.).
Вторая теорема подобия устанавливает, что для подобных явлений функциональная зависимость между критериями подобия (критериальное уравнение) имеет одно и то же значение. Таким образом, заменяя зависимость между величинами, характеризующими явление, зависимостью между критериями подобия можно получить обобщенную зависимость, пригодную для всех подобных явлений.
Третья теорема подобия устанавливает, что подобны те явления, у которых равны определяющие критерии подобия.
Определяющие критерии составляются из величин, входящих в условие однозначности явлений. К ним относятся: геометрическое подобие величин, характеризующих форму и размеры стенки, физические параметры среды и тела, тепловое и гидродинамическое подобие, граничные условия протекания процесса, временные условия протекания процесса и др.
Критерии подобия, в которое входят искомые величины, называются определяемыми или неопределяющими. Для процессов конвективного теплообмена определяющими критериями являются критерии 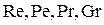 , а определяемым – критерий
, а определяемым – критерий 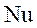 .
.
Порядок применения теории подобия к изучению явлений следующий.
Установив с помощь определяющих критериев подобия явлений по третьей теореме, затем на основании первой и второй теорем подобия устанавливается равенство неопределяющих определяемых критериев, а также функциональных зависимостей определяемых критериев от определяющих критериев, описывающих рассматриваемое явление (т. е. равенство критериальных уравнений).
